Comment effectuer une transformation Box-Cox dans R (avec exemples)

Une transformation box-cox est une méthode couramment utilisée pour transformer un ensemble de données non normalement distribué en un ensemble plusnormalement distribué .

L’idée de base derrière cette méthode est de trouver une valeur pour λ telle que les données transformées soient aussi proches que possible de la distribution normale, en utilisant la formule suivante :

• y(λ) = (y ^λ – 1) / λ si y ≠ 0
• y(λ) = log(y) si y = 0

Nous pouvons effectuer une transformation box-cox dans R en utilisant la fonction boxcox() de la bibliothèque MASS() . L’exemple suivant montre comment utiliser cette fonction dans la pratique.

Reportez-vous à cet article de l’Université du Connecticut pour un joli résumé du développement de la transformation Box-Cox.

Exemple : Transformation Box-Cox dans R

Le code suivant montre comment ajuster un modèle de régression linéaire à un ensemble de données, puis utiliser la fonction boxcox() pour trouver un lambda optimal pour transformer la variable de réponse et ajuster un nouveau modèle.

library(MASS)

#create data
y=c(1, 1, 1, 2, 2, 2, 2, 2, 2, 3, 3, 3, 6, 7, 8)
x=c(7, 7, 8, 3, 2, 4, 4, 6, 6, 7, 5, 3, 3, 5, 8)

#fit linear regression model
model <- lm(y~x)

#find optimal lambda for Box-Cox transformation 
bc <- boxcox(y ~ x)
(lambda <- bc$x[which.max(bc$y)])

[1] -0.4242424

#fit new linear regression model using the Box-Cox transformation
new_model <- lm(((y^lambda-1)/lambda) ~ x)

Le lambda optimal s’est avéré être -0,4242424 . Ainsi, le nouveau modèle de régression a remplacé la variable de réponse d’origine y par la variable y = (y ^-0,4242424 – 1) / -0,4242424.

Le code suivant montre comment créer deux tracés QQ dans R pour visualiser les différences de résidus entre les deux modèles de régression :

#define plotting area
op <- par(pty = "s", mfrow = c(1, 2))

#Q-Q plot for original model
qqnorm(model$residuals)
qqline(model$residuals)

#Q-Q plot for Box-Cox transformed model
qqnorm(new_model$residuals)
qqline(new_model$residuals)

#display both Q-Q plots
par(op)

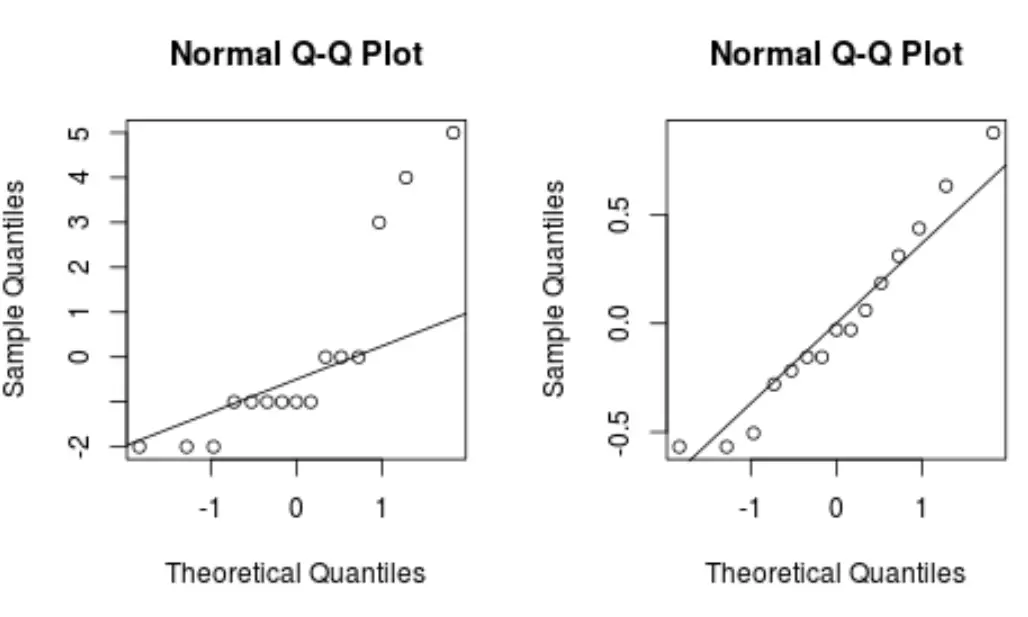
En règle générale, si les points de données se situent le long d’une ligne diagonale droite dans un tracé QQ, l’ensemble de données suit probablement une distribution normale.

Remarquez comment le modèle transformé en box-cox produit un tracé QQ avec une ligne beaucoup plus droite que le modèle de régression d’origine.

Cela indique que les résidus du modèle transformé en box-cox sont distribués beaucoup plus normalement, ce qui satisfait l’une des hypothèses de la régression linéaire .

Ressources additionnelles

Comment transformer des données dans R (Log, racine carrée, racine cubique)
Comment créer et interpréter un tracé QQ dans R
Comment effectuer un test de Shapiro-Wilk pour la normalité dans R