Comment effectuer le test de Friedman dans Excel

Le test de Friedman est une alternative non paramétrique à l’ ANOVA à mesures répétées . Il est utilisé pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes ou plus dans lesquels les mêmes sujets apparaissent dans chaque groupe.

Ce didacticiel explique comment effectuer le test de Friedman dans Excel.

Exemple : le test de Friedman dans Excel

Suivez les étapes suivantes pour effectuer le test de Friedman dans Excel.

Étape 1 : Saisissez les données.

Saisissez les données suivantes, qui montrent le temps de réaction (en secondes) de 10 patients prenant trois médicaments différents. Puisque chaque patient est mesuré sur chacun des trois médicaments, nous utiliserons le test de Friedman pour déterminer si le temps de réaction moyen diffère entre les médicaments.

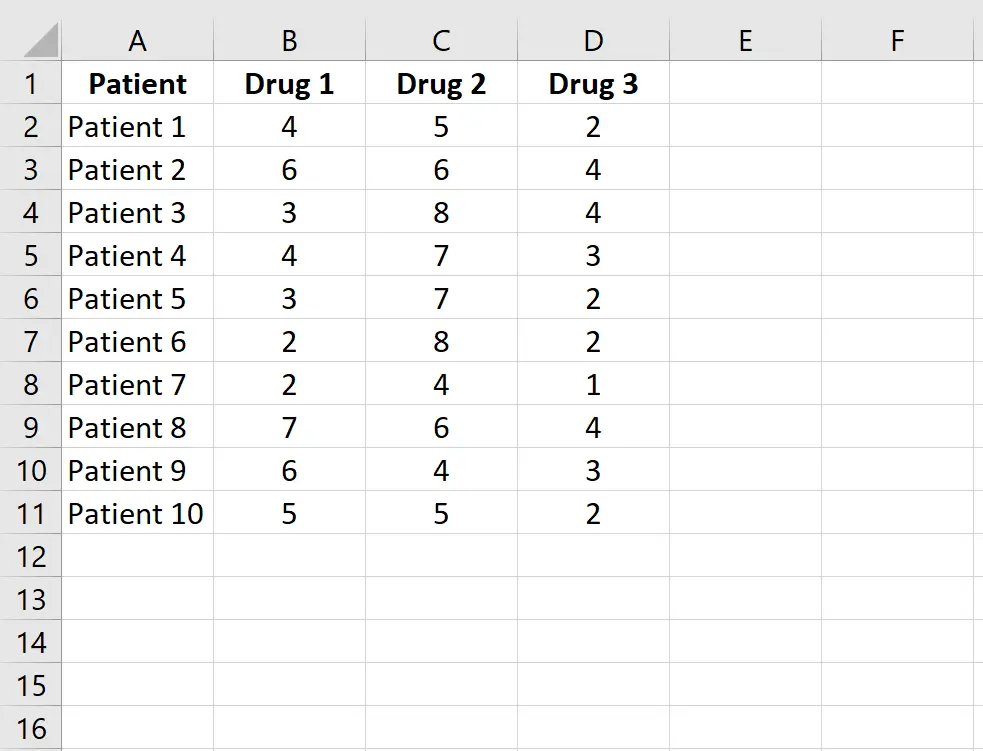
Étape 2 : Classez les données.

Ensuite, classez les valeurs de données dans chaque ligne par ordre croissant à l’aide de la fonction =RANK.AVG() . La formule suivante montre comment calculer le rang du temps de réponse du patient 1 au médicament 1 :

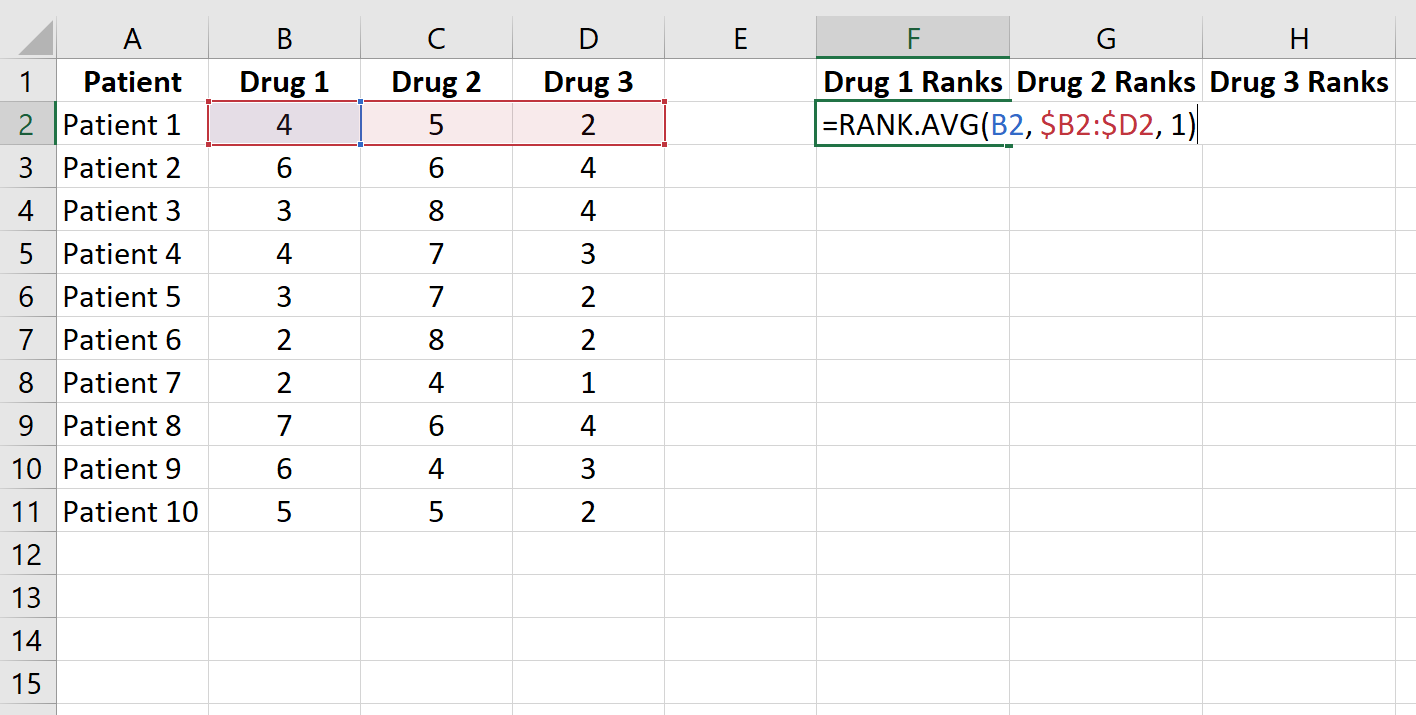
Copiez cette formule dans le reste des cellules :

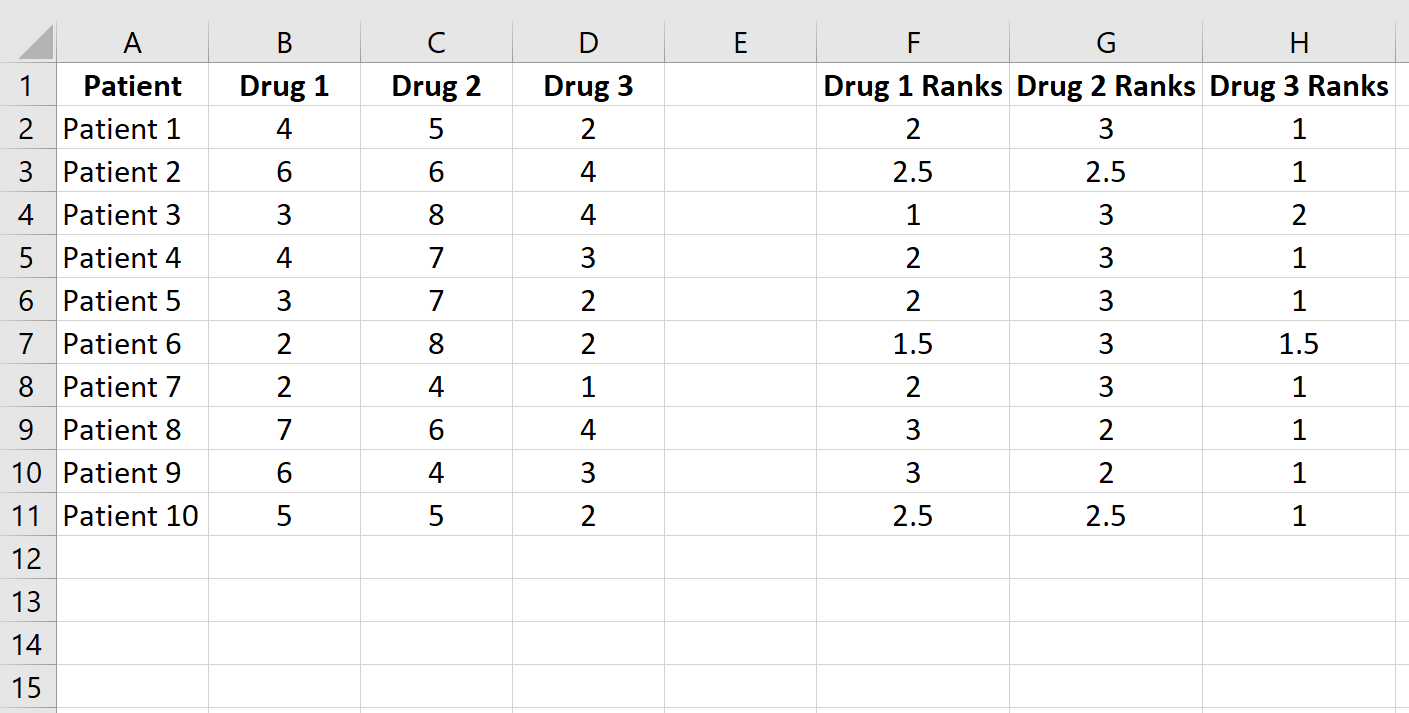
Ensuite, calculez la somme des rangs pour chaque colonne ainsi que la somme au carré des rangs :

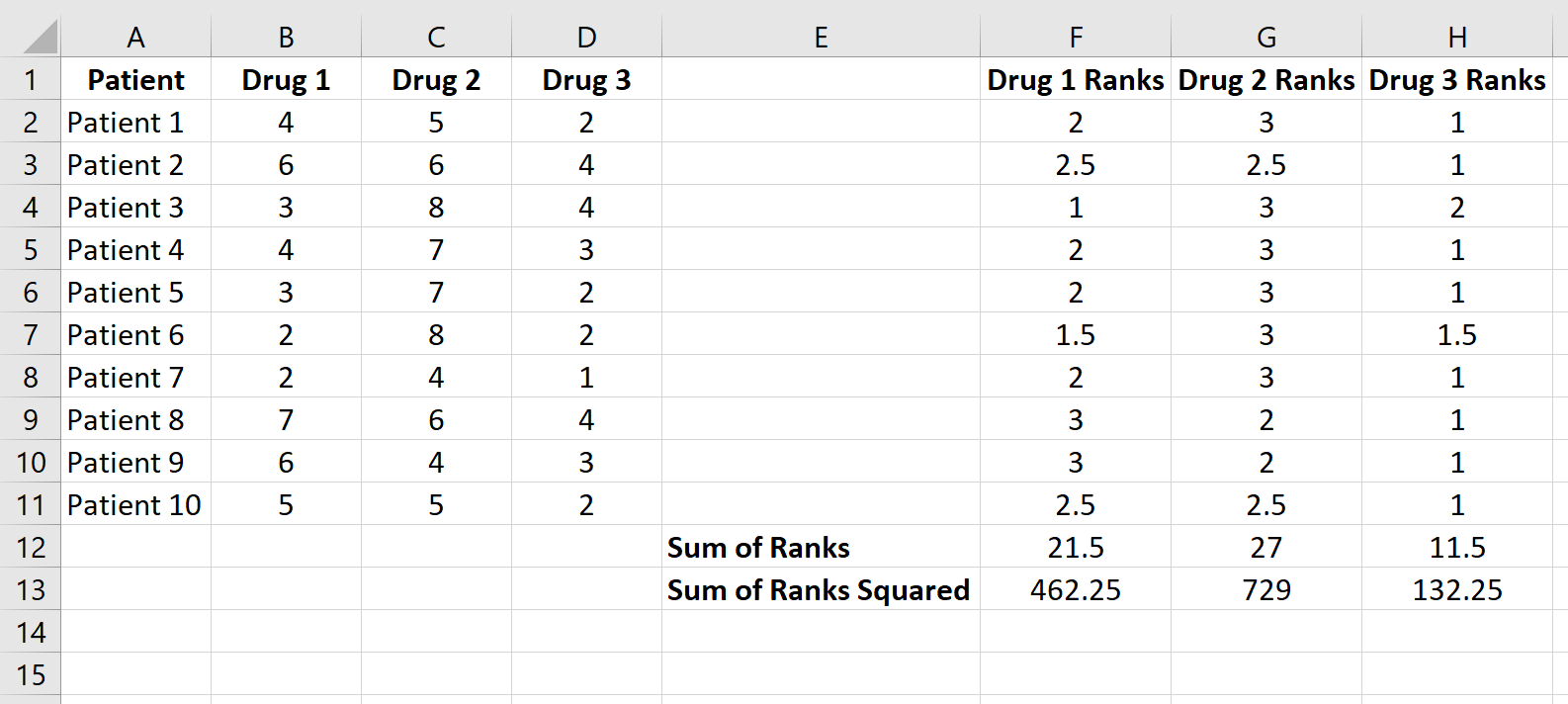
Étape 3 : Calculez la statistique de test et la valeur p correspondante.

La statistique du test est définie comme :

Q = 12/nk(k+1) * ΣR _j ² – 3n(k+1)

où:

• n = nombre de patients
• k = nombre de groupes de traitement
• R _j ² = somme des rangs pour le j ^ème groupe

Sous l’hypothèse nulle, Q suit une distribution du chi carré avec k-1 degrés de liberté.

La capture d’écran suivante montre les formules utilisées pour calculer la statistique de test, Q, et la valeur p correspondante :

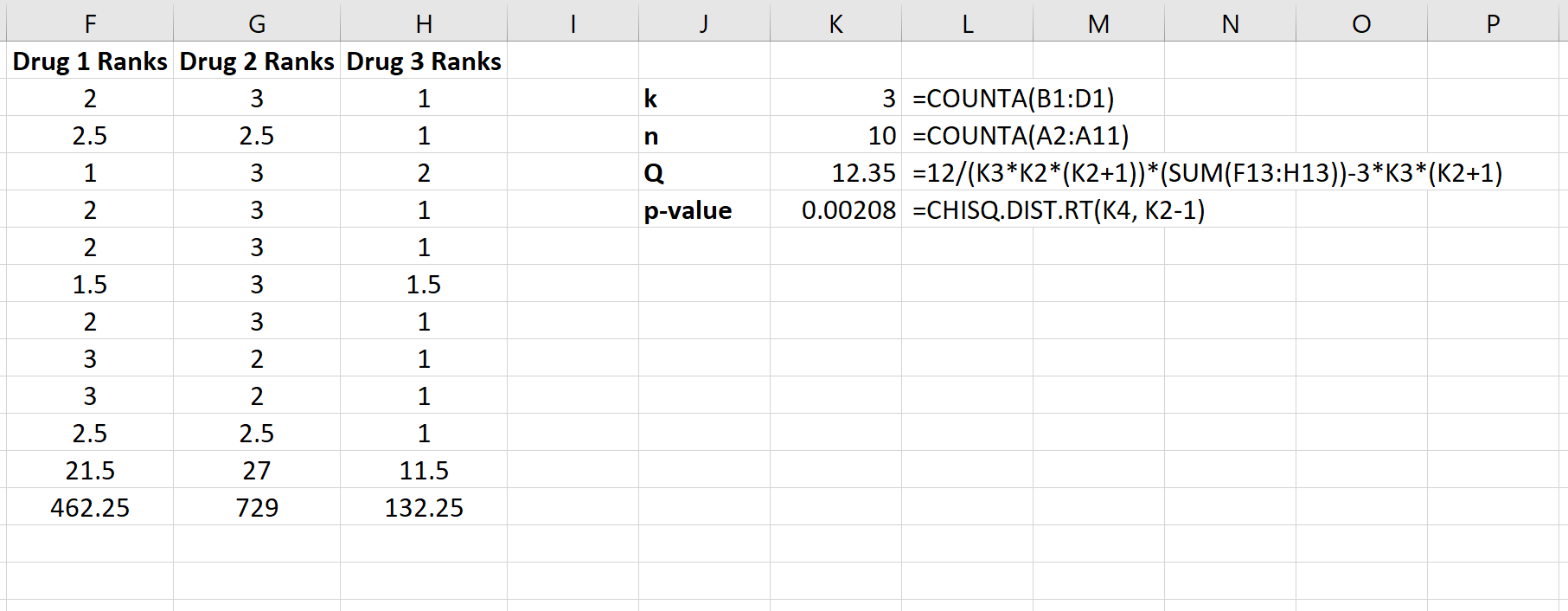
La statistique de test est Q = 12,35 et la valeur p correspondante est p = 0,00208 . Cette valeur étant inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle selon laquelle le temps de réponse moyen est le même pour les trois médicaments. Nous disposons de suffisamment de preuves pour conclure que le type de médicament utilisé entraîne des différences statistiquement significatives dans le temps de réponse.

Étape 4 : Rapportez les résultats.

Enfin, nous souhaitons rapporter les résultats du test. Voici un exemple de la façon de procéder :

Un test de Friedman a été réalisé sur 10 patients pour examiner l’effet de trois médicaments différents sur le temps de réponse. Chaque patient a utilisé chaque médicament une fois.

Les résultats ont montré que le type de médicament utilisé entraînait des différences statistiquement significatives dans le temps de réponse (Q = 12,35, p = 0,00208).