Régression des composantes principales dans R (étape par étape)

Étant donné un ensemble de p variables prédictives et une variable de réponse, la régression linéaire multiple utilise une méthode connue sous le nom de moindres carrés pour minimiser la somme des carrés résiduels (RSS) :

RSS = Σ(y _je – ŷ _je ) ²

où:

• Σ : Un symbole grec qui signifie somme
• y _i : la valeur de réponse réelle pour la ^ième observation
• ŷ _i : La valeur de réponse prédite basée sur le modèle de régression linéaire multiple

Cependant, lorsque les variables prédictives sont fortement corrélées, la multicolinéarité peut devenir un problème. Cela peut rendre les estimations des coefficients du modèle peu fiables et présenter une variance élevée.

Une façon d’éviter ce problème consiste à utiliser la régression en composantes principales , qui trouve M combinaisons linéaires (appelées « composantes principales ») des p prédicteurs d’origine, puis utilise les moindres carrés pour ajuster un modèle de régression linéaire en utilisant les composantes principales comme prédicteurs.

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression en composantes principales dans R.

Étape 1 : Charger les packages nécessaires

Le moyen le plus simple d’effectuer une régression des composantes principales dans R consiste à utiliser les fonctions du package pls .

#install pls package (if not already installed)
install.packages("pls")

load pls package
library(pls)

Étape 2 : Ajuster le modèle PCR

Pour cet exemple, nous utiliserons l’ensemble de données R intégré appelé mtcars qui contient des données sur différents types de voitures :

#view first six rows of mtcars dataset
head(mtcars)

                   mpg cyl disp  hp drat    wt  qsec vs am gear carb
Mazda RX4         21.0   6  160 110 3.90 2.620 16.46  0  1    4    4
Mazda RX4 Wag     21.0   6  160 110 3.90 2.875 17.02  0  1    4    4
Datsun 710        22.8   4  108  93 3.85 2.320 18.61  1  1    4    1
Hornet 4 Drive    21.4   6  258 110 3.08 3.215 19.44  1  0    3    1
Hornet Sportabout 18.7   8  360 175 3.15 3.440 17.02  0  0    3    2
Valiant           18.1   6  225 105 2.76 3.460 20.22  1  0    3    1

Pour cet exemple, nous allons ajuster un modèle de régression en composantes principales (PCR) en utilisant hp comme variable de réponse et les variables suivantes comme variables prédictives :

• mpg
• afficher
• merde
• poids
• qsec

Le code suivant montre comment adapter le modèle PCR à ces données. Notez les arguments suivants :

• scale=TRUE : Cela indique à R que chacune des variables prédictives doit être mise à l’échelle pour avoir une moyenne de 0 et un écart type de 1. Cela garantit qu’aucune variable prédictive n’a trop d’influence dans le modèle si elle est mesurée dans différentes unités. .
• validation=”CV” : Cela indique à R d’utiliser la validation croisée k-fold pour évaluer les performances du modèle. Notez que cela utilise k=10 plis par défaut. Notez également que vous pouvez spécifier « LOOCV » à la place pour effectuer une validation croisée Leave-One-Out .

#make this example reproducible
set.seed(1)

#fit PCR model
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=mtcars, scale=TRUE, validation="CV")

Étape 3 : Choisissez le nombre de composants principaux

Une fois que nous avons ajusté le modèle, nous devons déterminer le nombre de composants principaux qui méritent d’être conservés.

Pour ce faire, il suffit d’examiner l’erreur quadratique moyenne du test (RMSE de test) calculée par la validation croisée k :

#view summary of model fitting
summary(model)

Data: 	X dimension: 32 5 
	Y dimension: 32 1
Fit method: svdpc
Number of components considered: 5

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps
CV           69.66    44.56    35.64    35.83    36.23    36.67
adjCV        69.66    44.44    35.27    35.43    35.80    36.20

TRAINING: % variance explained
    1 comps  2 comps  3 comps  4 comps  5 comps
X     69.83    89.35    95.88    98.96   100.00
hp    62.38    81.31    81.96    81.98    82.03

Il y a deux tableaux intéressants dans le résultat :

1. VALIDATION : RMSEP

Ce tableau nous indique le test RMSE calculé par la validation croisée k-fold. Nous pouvons voir ce qui suit :

• Si nous utilisons uniquement le terme d’origine dans le modèle, le RMSE du test est de 69,66 .
• Si l’on ajoute la première composante principale, le test RMSE tombe à 44,56.
• Si l’on ajoute la deuxième composante principale, le test RMSE tombe à 35,64.

Nous pouvons voir que l’ajout de composants principaux supplémentaires entraîne en réalité une augmentation du RMSE du test. Ainsi, il apparaît qu’il serait optimal de n’utiliser que deux composantes principales dans le modèle final.

2. FORMATION : % d’écart expliqué

Ce tableau nous indique le pourcentage de variance de la variable réponse expliqué par les composantes principales. Nous pouvons voir ce qui suit :

• En utilisant uniquement la première composante principale, nous pouvons expliquer 69,83 % de la variation de la variable réponse.
• En ajoutant la deuxième composante principale, on peut expliquer 89,35 % de la variation de la variable réponse.

Notez que nous serons toujours en mesure d’expliquer plus de variance en utilisant plus de composantes principales, mais nous pouvons voir que l’ajout de plus de deux composantes principales n’augmente pas réellement le pourcentage de variance expliquée de beaucoup.

Nous pouvons également visualiser le test RMSE (avec le test MSE et R-carré) en fonction du nombre de composants principaux en utilisant la fonction validationplot() .

#visualize cross-validation plots
validationplot(model)
validationplot(model, val.type="MSEP")
validationplot(model, val.type="R2")

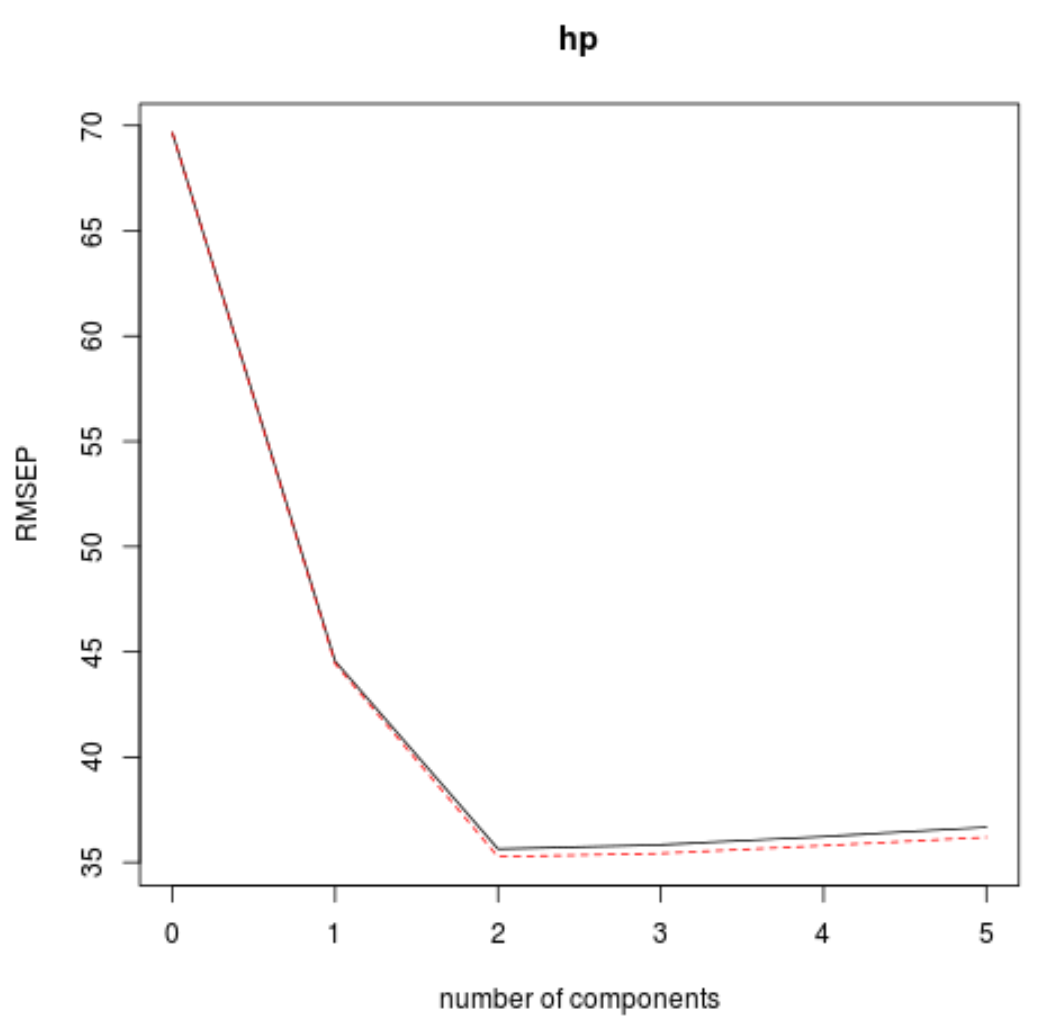
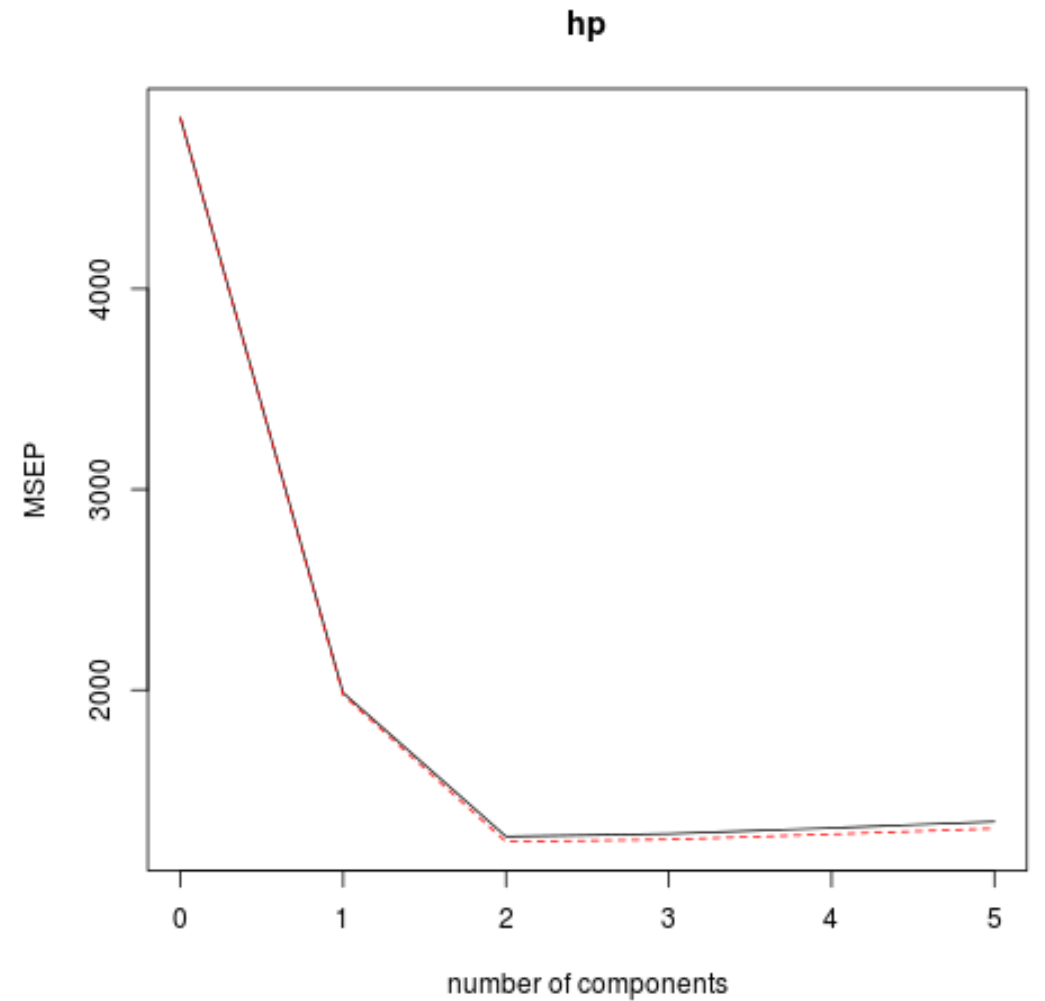
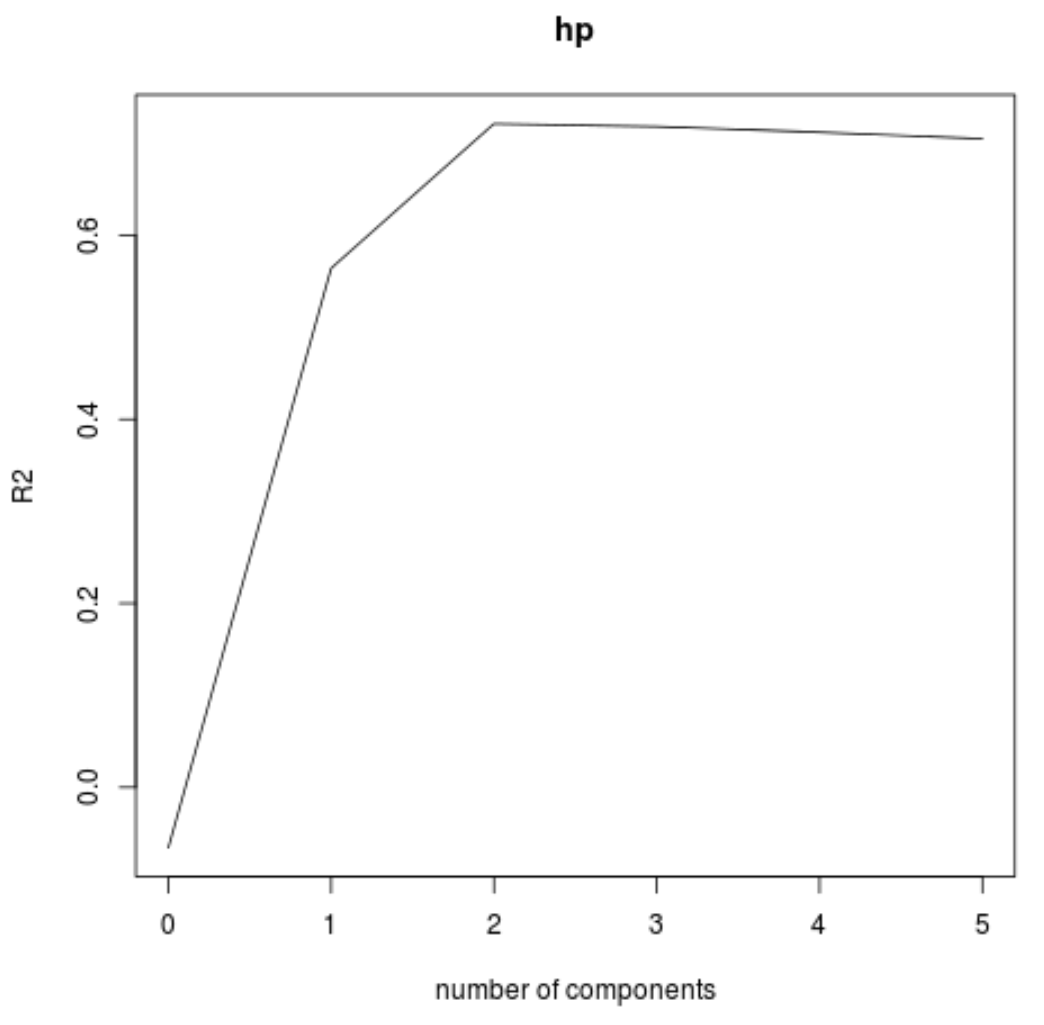
Dans chaque graphique, nous pouvons voir que l’ajustement du modèle s’améliore en ajoutant deux composantes principales, mais il a tendance à se détériorer lorsque nous ajoutons davantage de composantes principales.

Ainsi, le modèle optimal ne comprend que les deux premières composantes principales.

Étape 4 : Utiliser le modèle final pour faire des prédictions

Nous pouvons utiliser le modèle PCR final à deux composantes principales pour faire des prédictions sur de nouvelles observations.

Le code suivant montre comment diviser l’ensemble de données d’origine en un ensemble de formation et de test et utiliser le modèle PCR avec deux composants principaux pour faire des prédictions sur l’ensemble de test.

#define training and testing sets
train <- mtcars[1:25, c("hp", "mpg", "disp", "drat", "wt", "qsec")]
y_test <- mtcars[26:nrow(mtcars), c("hp")]
test <- mtcars[26:nrow(mtcars), c("mpg", "disp", "drat", "wt", "qsec")]
    
#use model to make predictions on a test set
model <- pcr(hp~mpg+disp+drat+wt+qsec, data=train, scale=TRUE, validation="CV")
pcr_pred <- predict(model, test, ncomp=2)

#calculate RMSE
sqrt(mean((pcr_pred - y_test)^2))

[1] 56.86549

On voit que le RMSE du test s’avère être 56.86549 . Il s’agit de l’écart moyen entre la valeur prédite de hp et la valeur observée de hp pour les observations de l’ensemble de tests.

L’utilisation complète du code R dans cet exemple peut être trouvée ici .