Une introduction rapide à la validation croisée Leave-One-Out (LOOCV)

Pour évaluer les performances d’un modèle sur un ensemble de données, nous devons mesurer dans quelle mesure les prédictions faites par le modèle correspondent aux données observées.

La façon la plus courante de mesurer cela consiste à utiliser l’erreur quadratique moyenne (MSE), qui est calculée comme suit :

MSE = (1/n)*Σ(y _je – f(x _je )) ²

où:

• n : nombre total d’observations
• y _i : La valeur de réponse de la ^ième observation
• f(x _i ) : La valeur de réponse prédite de la i ^ème observation

Plus les prédictions du modèle sont proches des observations, plus la MSE sera faible.

En pratique, nous utilisons le processus suivant pour calculer le MSE d’un modèle donné :

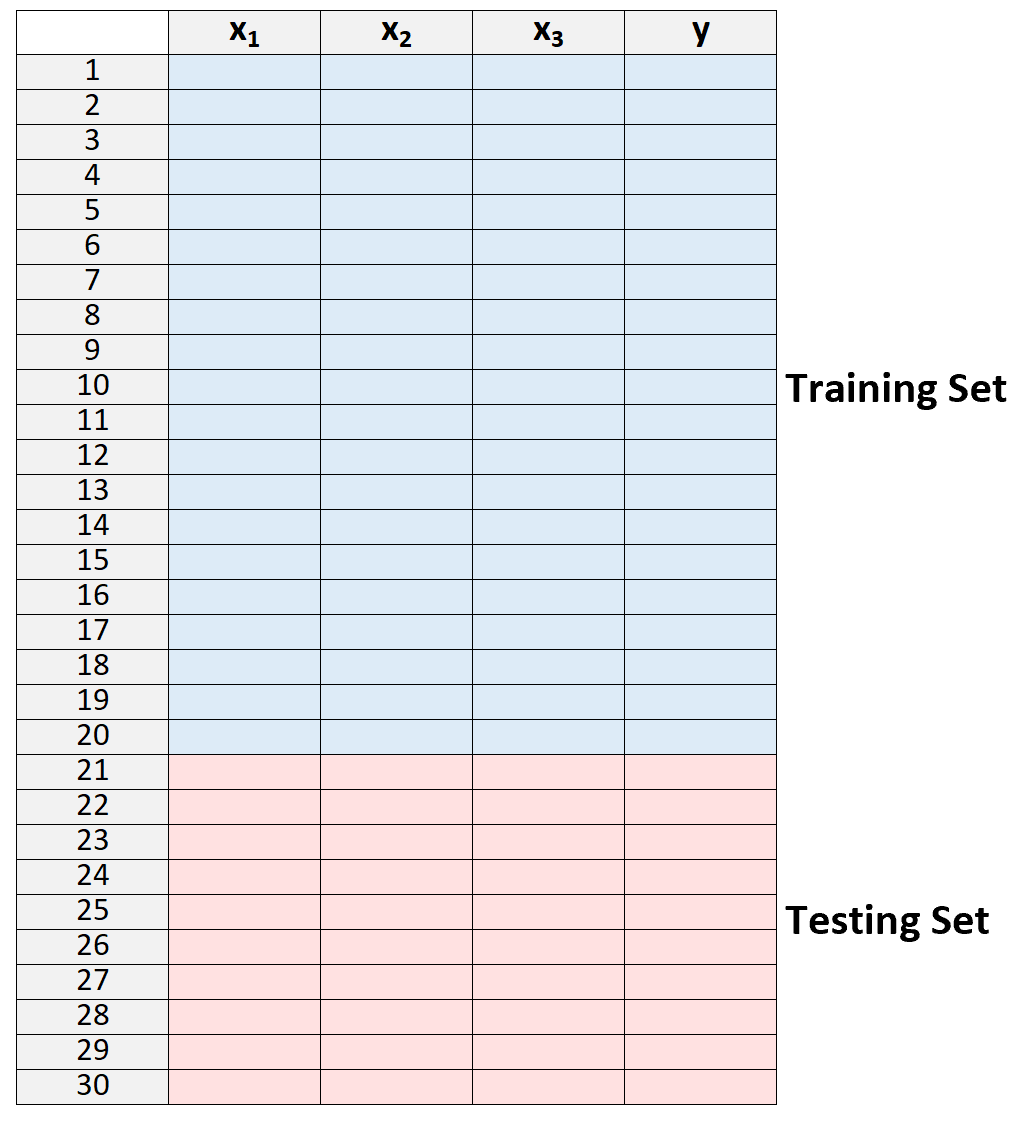
1. Divisez un ensemble de données en un ensemble de formation et un ensemble de test.

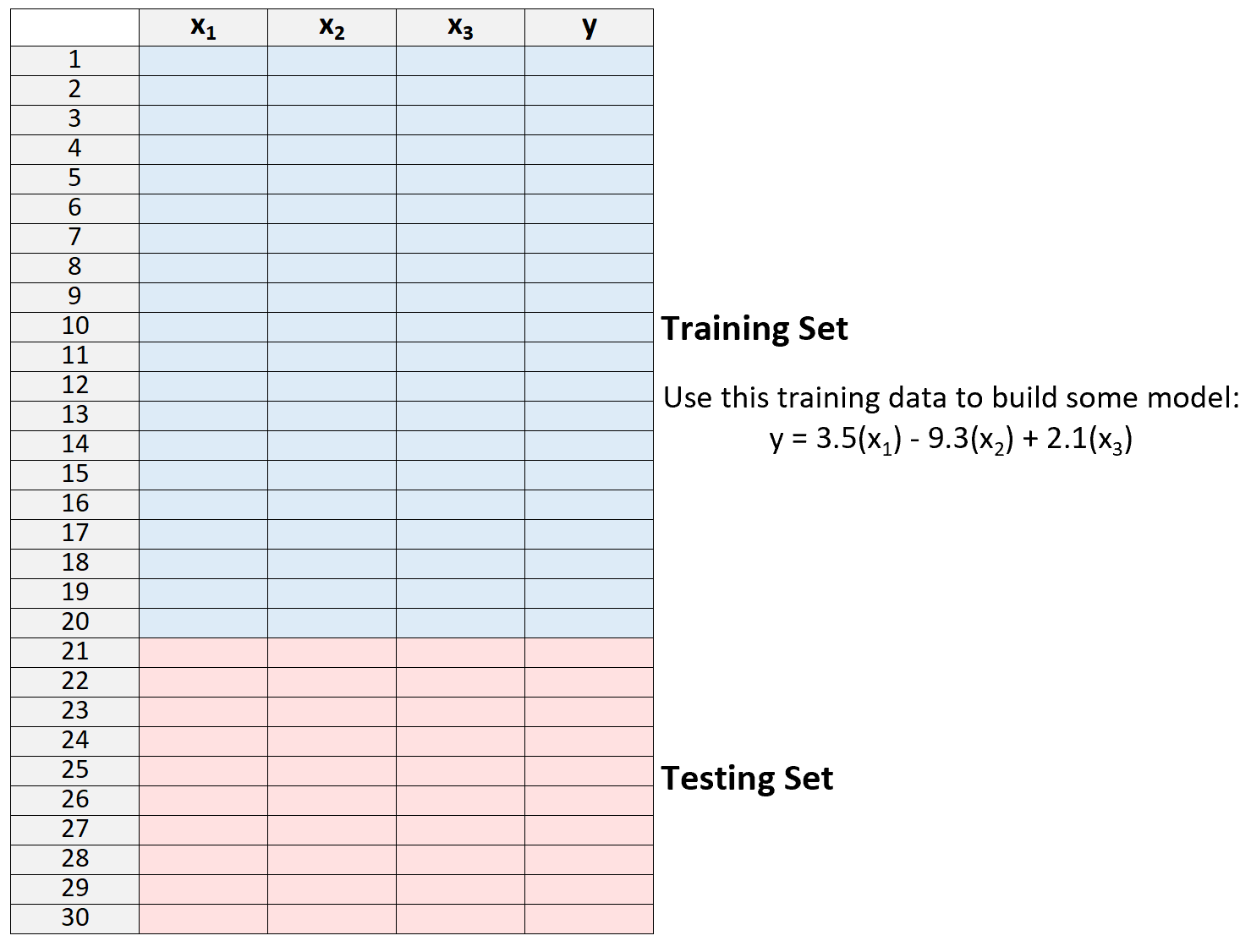
2. Créez le modèle en utilisant uniquement les données de l’ensemble de formation.

3. Utilisez le modèle pour faire des prédictions sur l’ensemble de test et mesurer le MSE – c’est ce qu’on appelle le MSE de test .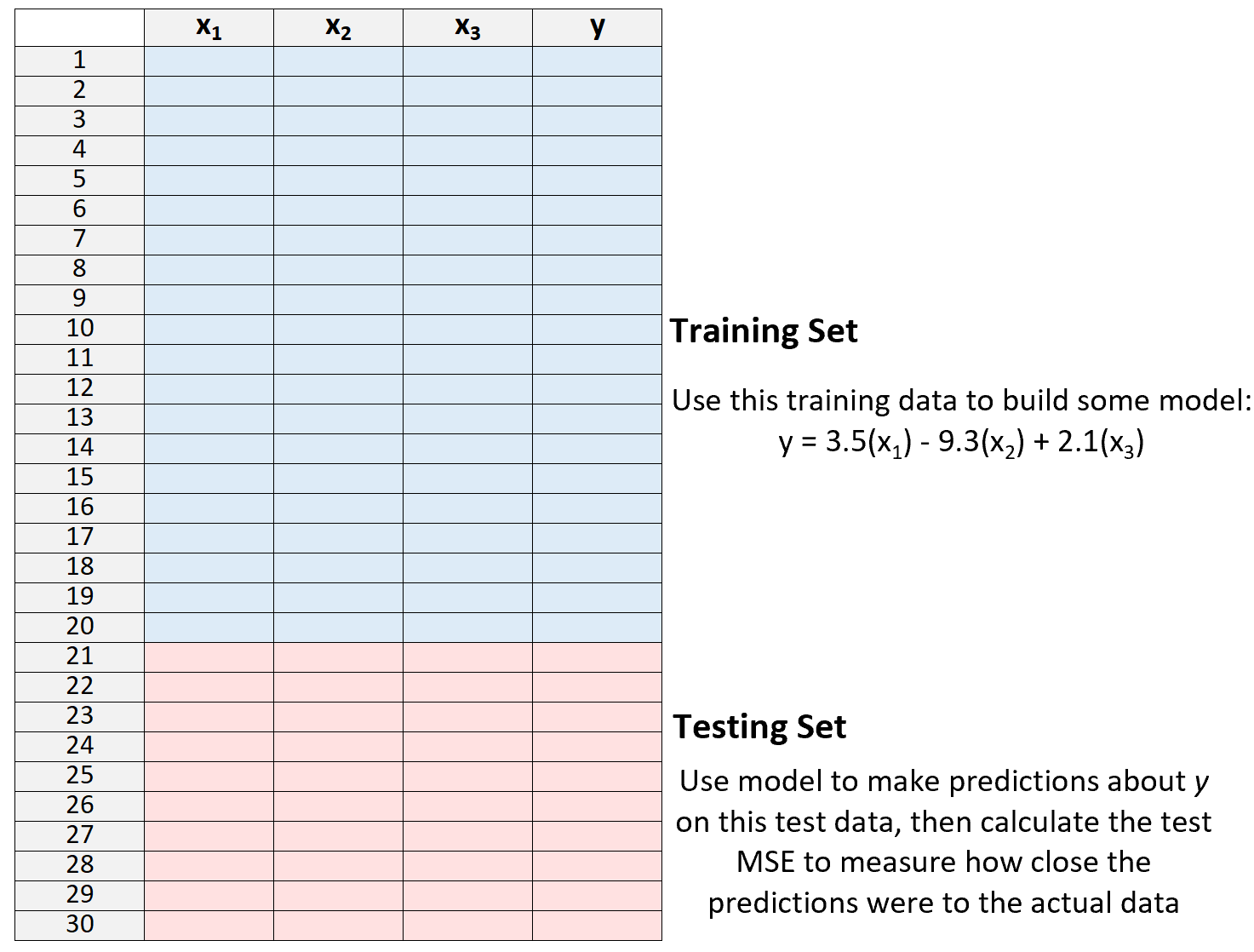

Le test MSE nous donne une idée des performances d’un modèle sur des données qu’il n’a pas vues auparavant, c’est-à-dire des données qui n’ont pas été utilisées pour « entraîner » le modèle.

Cependant, l’inconvénient de l’utilisation d’un seul ensemble de tests est que le MSE du test peut varier considérablement en fonction des observations utilisées dans les ensembles de formation et de test.

Il est possible que si nous utilisons un ensemble d’observations différent pour l’ensemble d’entraînement et l’ensemble de test, notre MSE de test pourrait s’avérer beaucoup plus grand ou plus petit.

Une façon d’éviter ce problème consiste à ajuster un modèle plusieurs fois en utilisant à chaque fois un ensemble de formation et de test différent, puis à calculer le MSE du test comme étant la moyenne de tous les MSE du test.

Cette méthode générale est connue sous le nom de validation croisée et une forme spécifique de celle-ci est connue sous le nom de validation croisée Leave-One-Out .

Validation croisée Leave-One-Out

La validation croisée Leave-one-out utilise l’approche suivante pour évaluer un modèle :

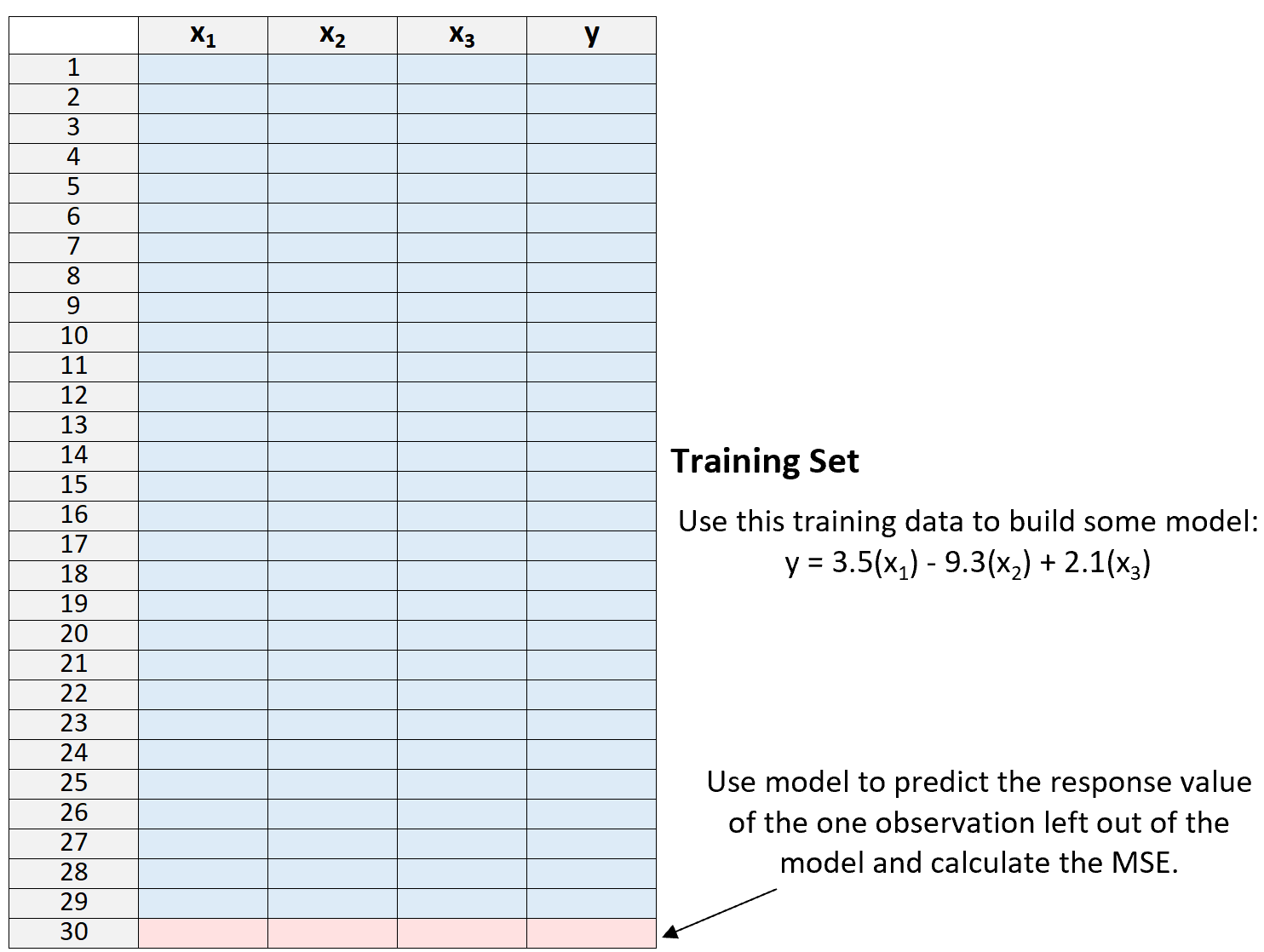
1. Divisez un ensemble de données en un ensemble de formation et un ensemble de test, en utilisant toutes les observations sauf une dans le cadre de l’ensemble de formation :

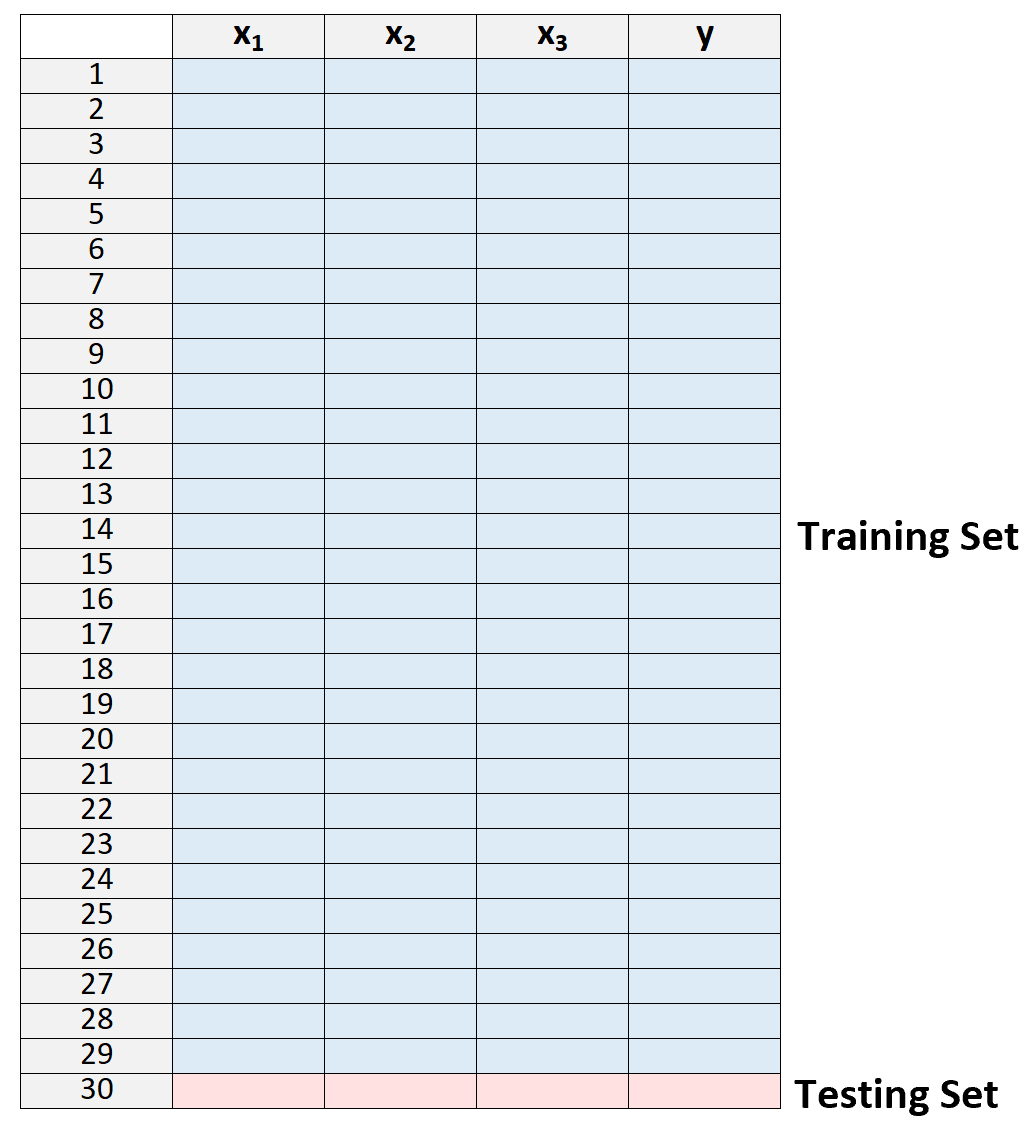
Notez que nous ne laissons qu’une seule observation « en dehors » de l’ensemble d’apprentissage. C’est là que la méthode reçoit le nom de validation croisée « leave-one-out ».

2. Créez le modèle en utilisant uniquement les données de l’ensemble de formation.

3. Utilisez le modèle pour prédire la valeur de réponse de la seule observation exclue du modèle et calculez le MSE.

4. Répétez le processus n fois.

Enfin, nous répétons ce processus n fois (où n est le nombre total d’observations dans l’ensemble de données), en laissant de côté à chaque fois une observation différente de l’ensemble d’apprentissage.

Nous calculons ensuite le MSE du test comme étant la moyenne de tous les MSE du test :

Test MSE = (1/n)*ΣMSE _i

où:

• n : le nombre total d’observations dans l’ensemble de données
• MSEi : le MSE de test au cours de la ^ième période d’ajustement du modèle.

Avantages et inconvénients de LOOCV

La validation croisée Leave-one-out offre les avantages suivants :

• Il fournit une mesure beaucoup moins biaisée du test MSE par rapport à l’utilisation d’un seul ensemble de tests, car nous ajustons à plusieurs reprises un modèle à un ensemble de données contenant n-1 observations.
• Il a tendance à ne pas surestimer le MSE du test par rapport à l’utilisation d’un seul ensemble de tests.

Cependant, la validation croisée sans intervention présente les inconvénients suivants :

• L’utilisation de ce processus peut prendre beaucoup de temps lorsque n est grand.
• Cela peut également prendre du temps si un modèle est particulièrement complexe et prend beaucoup de temps à s’adapter à un ensemble de données.
• Cela peut être coûteux en calcul.

Heureusement, l’informatique moderne est devenue si efficace dans la plupart des domaines que LOOCV est une méthode beaucoup plus raisonnable à utiliser qu’il y a de nombreuses années.

Notez que LOOCV peut également être utilisé dans des contextes de régression et de classification . Pour les problèmes de régression, il calcule le test MSE comme étant la différence quadratique moyenne entre les prédictions et les observations, tandis que dans les problèmes de classification, il calcule le test MSE comme étant le pourcentage d’observations correctement classées au cours des n ajustements répétés du modèle.

Comment exécuter LOOCV en R & Python

Les didacticiels suivants fournissent des exemples étape par étape sur la façon d’exécuter LOOCV pour un modèle donné en R et Python :

Validation croisée Leave-One-Out dans R
Validation croisée Leave-One-Out en Python