Comment effectuer un test Cramer-Von Mises dans R (avec exemples)

Le test de Cramer-Von Mises est utilisé pour déterminer si un échantillon provient ou non d’unedistribution normale .

Ce type de test est utile pour déterminer si un ensemble de données donné provient ou non d’une distribution normale, ce qui est une hypothèse couramment utilisée dans de nombreux tests statistiques, notamment la régression , l’ANOVA , les tests t et bien d’autres.

Nous pouvons facilement effectuer un test Cramer-Von Mises en utilisant la fonction cvm.test() du package goftest dans R.

L’exemple suivant montre comment utiliser cette fonction dans la pratique.

Exemple 1 : Test de Cramer-Von Mises sur des données normales

Le code suivant montre comment effectuer un test Cramer-Von Mises sur un ensemble de données avec une taille d’échantillon n=100 :

library(goftest)

#make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Cramer-Von Mises test for normality
cvm.test(data, 'pnorm')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:  data
omega2 = 0.078666, p-value = 0.7007

La valeur p du test s’avère être de 0,7007 .

Puisque cette valeur n’est pas inférieure à 0,05, nous pouvons supposer que les données de l’échantillon proviennent d’une population normalement distribuée.

Ce résultat ne devrait pas être surprenant puisque nous avons généré les exemples de données à l’aide de la fonction rnorm() , qui génère des valeurs aléatoires à partir d’une distribution normale standard .

Connexe : Un guide sur dnorm, pnorm, qnorm et rnorm dans R

Nous pouvons également produire un histogramme pour vérifier visuellement que les données de l’échantillon sont normalement distribuées :

hist(data, col='steelblue')

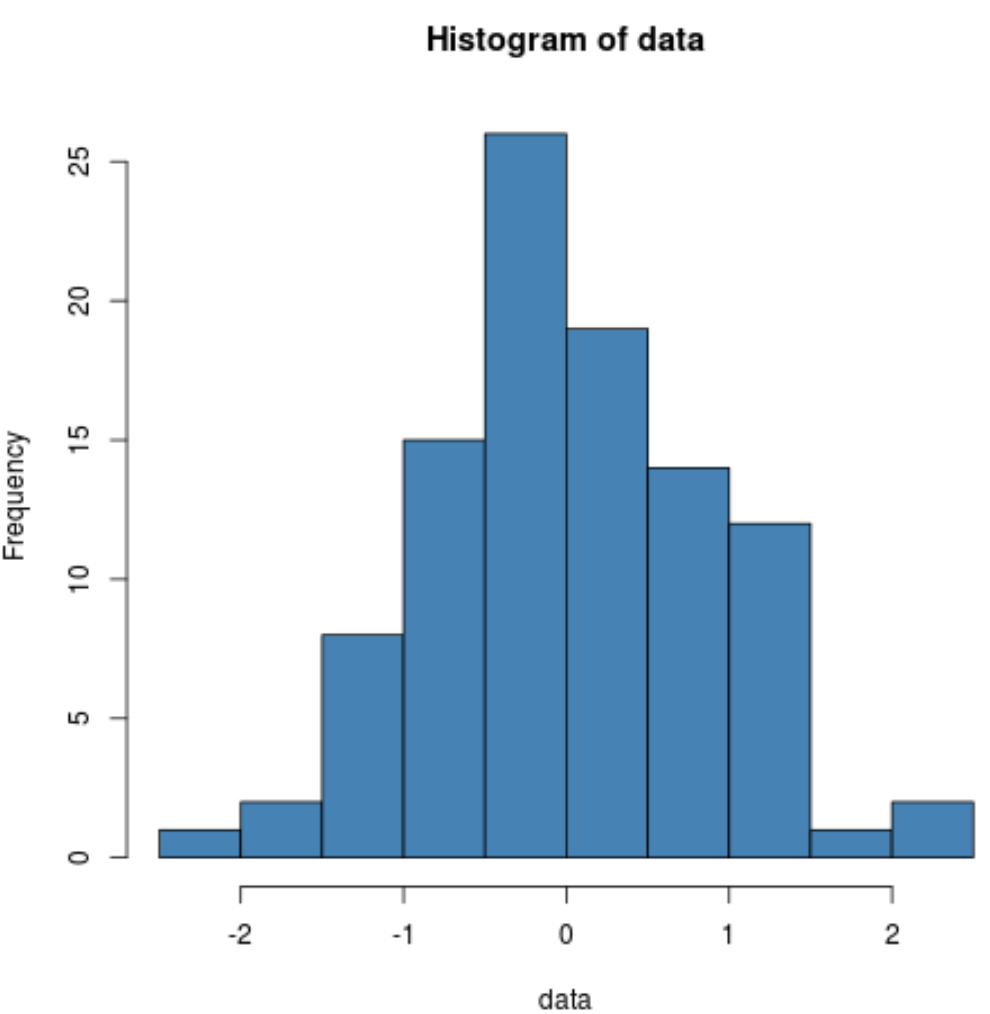
Nous pouvons voir que la distribution est assez en forme de cloche avec un pic au centre de la distribution, ce qui est typique des données normalement distribuées.

Exemple 2 : Test de Cramer-Von Mises sur des données non normales

Le code suivant montre comment effectuer un test de Cramer-Von Mises sur un ensemble de données avec une taille d’échantillon de 100 dans lequel les valeurs sont générées aléatoirement à partir d’une distribution de Poisson :

library(goftest)

#make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Cramer-Von Mises test for normality
cvm.test(data, 'pnorm')

	Cramer-von Mises test of goodness-of-fit
	Null hypothesis: Normal distribution
	Parameters assumed to be fixed

data:  data
omega2 = 27.96, p-value < 2.2e-16

La valeur p du test s’avère extrêmement faible.

Puisque cette valeur est inférieure à 0,05, nous disposons de suffisamment de preuves pour affirmer que les données de l’échantillon ne proviennent pas d’une population normalement distribuée.

Ce résultat ne devrait pas être surprenant puisque nous avons généré les exemples de données à l’aide de la fonction rpois() , qui génère des valeurs aléatoires à partir d’une distribution de Poisson.

Connexe : Un guide des dpois, ppois, qpois et rpois dans R

Nous pouvons également produire un histogramme pour voir visuellement que les données de l’échantillon ne sont pas normalement distribuées :

hist(data, col='coral2')

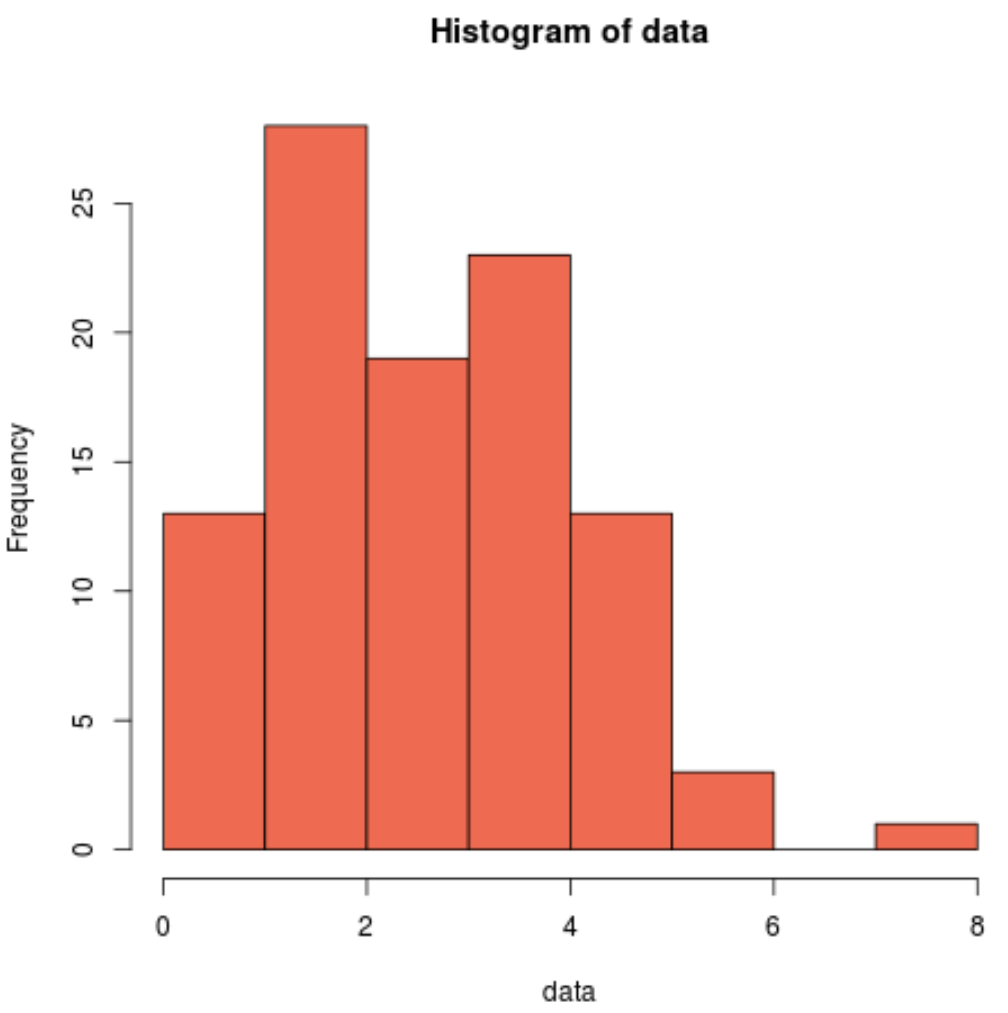
Nous pouvons voir que la distribution est asymétrique à droite et n’a pas la « forme de cloche » typique associée à une distribution normale.

Ainsi, notre histogramme correspond aux résultats du test Cramer-Von Mises et confirme que nos données d’échantillon ne proviennent pas d’une distribution normale.

Que faire avec des données non normales

Si un ensemble de données donné n’est pas normalement distribué, nous pouvons souvent effectuer l’une des transformations suivantes pour le rendre plus normal :

1. Transformation du journal : transformez la variable de réponse de y en log(y) .

2. Transformation racine carrée : Transformez la variable de réponse de y en √y .

3. Transformation de racine cubique : transformez la variable de réponse de y en y ^1/3 .

En effectuant ces transformations, la variable de réponse se rapproche généralement de la distribution normale.

Référez-vous à ce tutoriel pour voir comment réaliser ces transformations en pratique.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tests de normalité dans R :

Comment effectuer un test Shapiro-Wilk dans R
Comment effectuer un test d’Anderson-Darling dans R
Comment effectuer un test de Kolmogorov-Smirnov dans R