Comment utiliser la distribution triangulaire dans R (avec exemples)

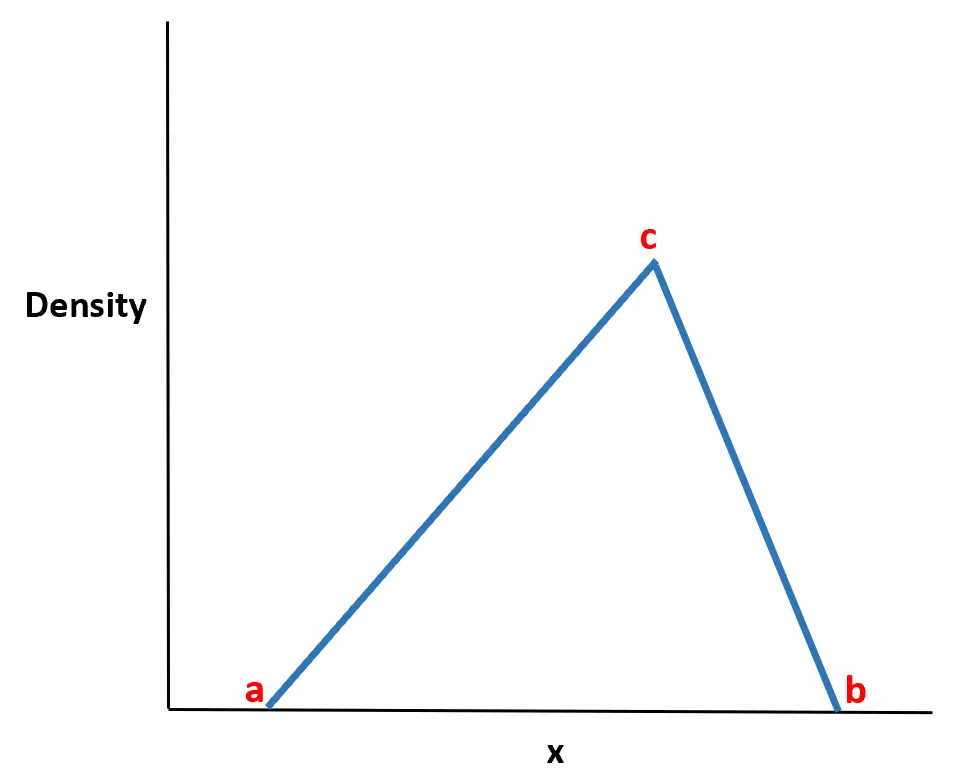
La distribution triangulaire est une distribution de probabilité continue avec une fonction de densité de probabilité en forme de triangle.

Il est défini par trois valeurs :

• La valeur minimale a
• La valeur maximale b
• La valeur maximale c

Pour calculer les probabilités de la distribution triangulaire dans R, nous pouvons utiliser la fonction ptri( ) du package EnvStats , qui utilise la syntaxe suivante :

ptri(q, min = 0, max = 1, mode = 1/2)

où:

• q : Quantile d’intérêt
• min : La valeur minimale de la distribution
• max : La valeur maximale de la distribution
• mode : La valeur crête de la distribution

Les exemples suivants montrent comment utiliser cette fonction en pratique dans R.

Exemple 1 : Calcul d’une probabilité inférieure à une certaine valeur

Supposons qu’un restaurant estime que ses ventes totales pour la semaine à venir seront d’un minimum de 10 000 $, d’un maximum de 30 000 $ et très probablement de 25 000 $.

Quelle est la probabilité que le restaurant réalise un chiffre d’affaires total inférieur à 20 000 $ ?

Nous pouvons utiliser le code suivant pour calculer cette probabilité :

library(EnvStats)

#calculate probability
ptri(q = 20000, min = 10000, max = 30000, mode = 25000)

[1] 0.3333333

La probabilité que le restaurant réalise un chiffre d’affaires total inférieur à 20 000 $ est de 0,333 .

Exemple 2 : Calcul d’une probabilité supérieure à une certaine valeur

Supposons qu’un magasin estime que le nombre de clients qui entreront au cours d’une semaine donnée sera d’un minimum de 500, d’un maximum de 2 000 et très probablement de 1 200.

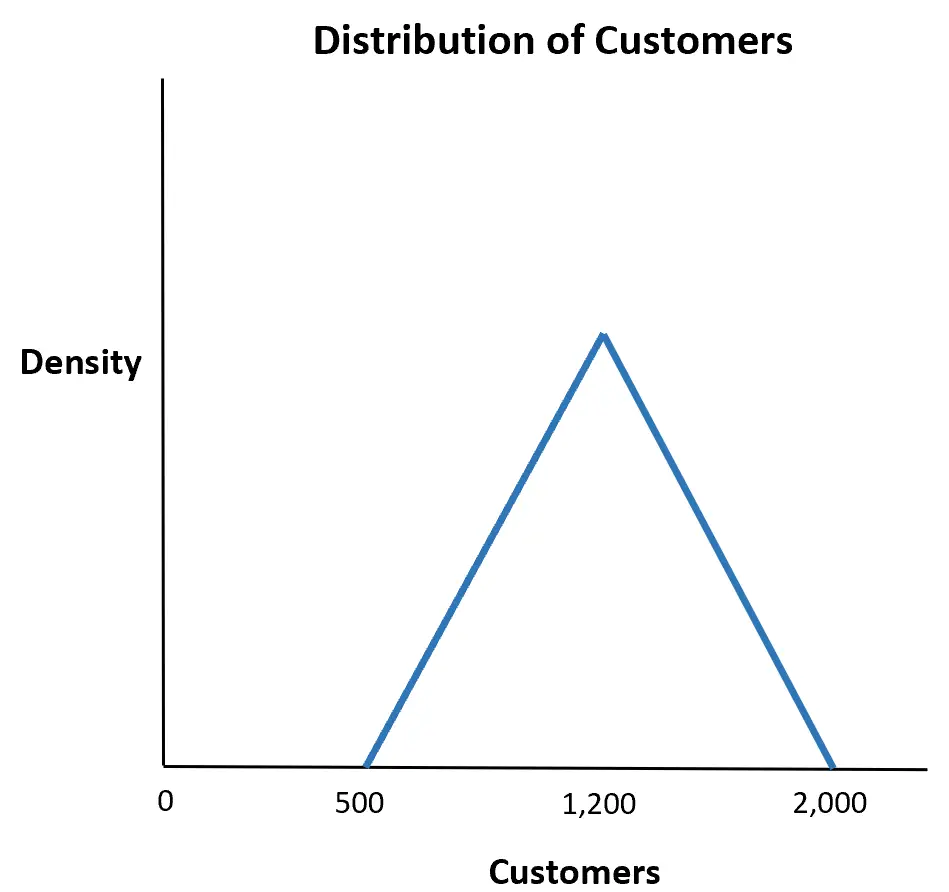
Quelle est la probabilité que plus de 1 500 clients entrent dans le magasin au cours d’une semaine donnée ?

Nous pouvons utiliser le code suivant pour calculer cette probabilité :

library(EnvStats)

#calculate probability
1 - ptri(q = 1500, min = 500, max = 2000, mode = 1200)

[1] 0.2083333

La probabilité que plus de 1 500 clients entrent dans le magasin est d’environ 0,208.

Remarque : Vous pouvez trouver la documentation complète de la fonction ptri() ici .

Ressources additionnelles

Les didacticiels suivants expliquent comment utiliser d’autres distributions de probabilité dans R :

Comment utiliser la distribution normale dans R
Comment utiliser la distribution binomiale dans R
Comment utiliser la distribution de Poisson dans R
Comment utiliser la distribution multinomiale dans R