Distribution uniforme discrète
Cet article explique ce qu’est la distribution uniforme discrète et quelle est sa formule caractéristique. De même, vous pourrez voir la représentation graphique de la distribution uniforme discrète et quelles sont ses propriétés.
Qu’est-ce que la distribution uniforme discrète ?
La distribution uniforme discrète est une distribution de probabilité discrète dans laquelle toutes les valeurs sont équiprobables, c’est-à-dire que dans une distribution uniforme discrète, toutes les valeurs ont la même probabilité de se produire.
Par exemple, le lancer d’un dé peut être défini avec une distribution uniforme discrète, puisque tous les résultats possibles (1, 2, 3, 4, 5 ou 6) ont la même probabilité d’occurrence.
En général, une distribution uniforme discrète a deux paramètres caractéristiques, a et b , qui définissent la plage de valeurs possibles que peut prendre la distribution. Ainsi, lorsqu’une variable est définie par une distribution uniforme discrète, elle s’écrit Uniform(a,b) .
La distribution uniforme discrète peut être utilisée pour décrire des expériences aléatoires, car si tous les résultats ont la même probabilité, cela signifie que l’expérience est aléatoire.
Formule de distribution uniforme discrète
Maintenant que nous connaissons la définition de la distribution uniforme discrète, nous allons voir quelle est la formule qui nous permet de calculer la probabilité d’apparition des valeurs d’une distribution de ce type.
La fonction de probabilité d’une distribution uniforme discrète est constante et sa valeur est égale à un sur le nombre total de résultats possibles. Ainsi, la formule de la distribution uniforme discrète est la suivante :
![P[X=x]=\cfrac{1}{n}=\cfrac{1}{b-a+1}](https://statorials.org/wp-content/ql-cache/quicklatex.com-e859f9b02aa8706b23092d8119ab3c82_l3.png "Rendered by QuickLaTeX.com")
D’autre part, la formule de la fonction de probabilité cumulative de la distribution uniforme discrète est la suivante :
![P[X\leq x]=\cfrac{\lfloor x \rfloor -a + 1}{b-a+1}](https://statorials.org/wp-content/ql-cache/quicklatex.com-1e504fea34915fd188d59fac9efd70ed_l3.png "Rendered by QuickLaTeX.com")
Où
et
sont les paramètres caractéristiques de la distribution uniforme discrète.
Diagramme de distribution uniforme discret
Étant donné que la distribution uniforme discrète ne peut prendre que certaines valeurs dans un intervalle, sa représentation graphique est constituée de points. De plus, toutes les probabilités sont égales, donc tous les points de la distribution uniforme discrète ont la même coordonnée verticale.
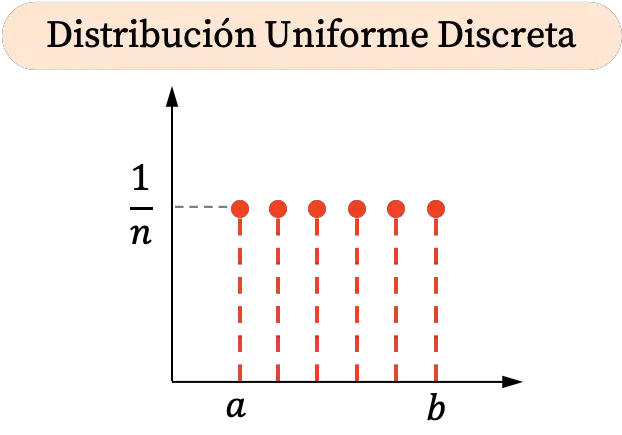
D’autre part, le graphique de probabilité cumulée de la distribution uniforme discrète est le suivant :
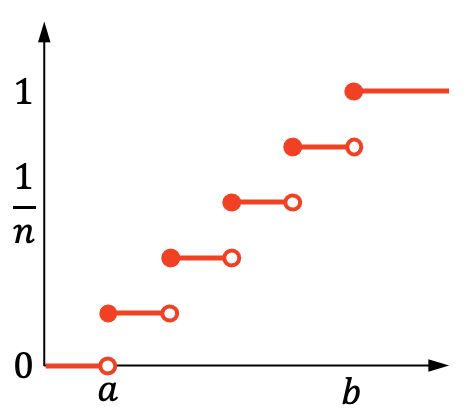
Caractéristiques de la distribution uniforme discrète
La distribution uniforme discrète répond aux caractéristiques suivantes :
- La distribution uniforme discrète est définie par deux paramètres entiers, a et b , qui déterminent la plage des valeurs possibles de la distribution.
![\begin{array}{c} X\sim \text{Uniforme}(a,b)\\[2ex]b\geq a\\[2ex]n=b-a+1\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-4937817442028ed33c270680f7eb4664_l3.png "Rendered by QuickLaTeX.com")
- La moyenne d’une distribution uniforme discrète est égale à la somme de ses deux paramètres caractéristiques divisée par deux.
![E[X]=\cfrac{a+b}{2}](https://statorials.org/wp-content/ql-cache/quicklatex.com-96d92a77b5dce5d38b2b2f3b79ac09a3_l3.png "Rendered by QuickLaTeX.com")
- La médiane d’une distribution uniforme discrète est équivalente à sa moyenne, elle est donc calculée avec la même expression :
- La variance d’une distribution uniforme discrète est égale au carré du nombre total de résultats moins un divisé par douze.
- La distribution uniforme discrète est symétrique par rapport à sa moyenne, par conséquent, le coefficient d’asymétrie de cette distribution de probabilité est nul.
- L’aplatissement de la distribution uniforme discrète peut être calculé à l’aide de l’expression suivante :
Distribution uniforme discrète et distribution uniforme continue
Enfin, nous verrons quelle est la différence entre une distribution uniforme discrète et une distribution uniforme continue, puisqu’il s’agit de deux types de distributions de probabilité similaires mais avec une différence substantielle.
La différence entre une distribution uniforme discrète et une distribution uniforme continue réside dans leurs valeurs possibles. La distribution uniforme discrète ne peut prendre que certaines valeurs dans un intervalle, tandis que la distribution uniforme continue peut prendre n’importe quelle valeur dans l’intervalle dans lequel elle est définie.
En général, les distributions uniformes discrètes ne peuvent prendre que des valeurs entières, tandis que les distributions uniformes continues peuvent également prendre des valeurs décimales.
à propos de l'auteur
Pr Amélia Rodriguez
En mettant l'accent sur l'apprentissage interactif et les applications pratiques, la professeure Amélia Rodriguez propose des tutoriels complets et des exemples concrets pour rendre les concepts de probabilité accessibles et pertinents pour la vie de ses étudiants. Lire plus