5 exemples de données bivariées dans la vie réelle

Les données bivariées font référence à un ensemble de données contenant exactement deux variables.

Ce type de données apparaît constamment dans des situations réelles et nous utilisons généralement les méthodes suivantes pour analyser ce type de données :

• Nuages de points
• Coefficients de corrélation
• Régression linéaire simple

Les exemples suivants montrent différents scénarios dans lesquels des données bivariées apparaissent dans la vie réelle.

Exemple 1 : Entreprise

Les entreprises collectent souvent des données bivariées sur l’argent total dépensé en publicité et les revenus totaux.

Par exemple, une entreprise peut collecter les données suivantes pendant 12 trimestres de ventes consécutifs :

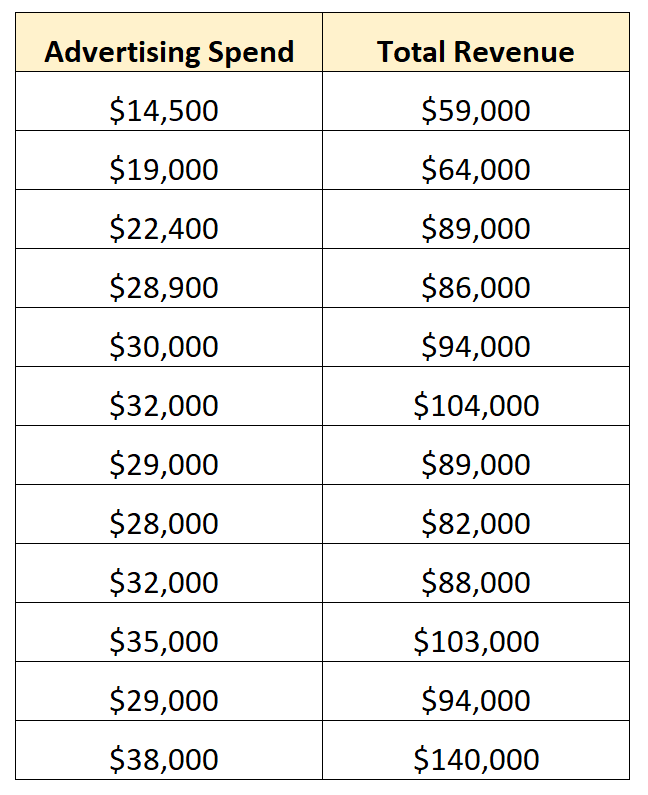
Il s’agit d’un exemple de données bivariées car elles contiennent des informations sur exactement deux variables : les dépenses publicitaires et les revenus totaux.

L’entreprise peut décider d’adapter un modèle de régression linéaire simple à cet ensemble de données et trouver le modèle ajusté suivant :

Revenu total = 14 942,75 + 2,70* (dépenses publicitaires)

Cela indique à l’entreprise que pour chaque dollar supplémentaire dépensé en publicité, les revenus totaux augmentent en moyenne de 2,70 $.

Exemple 2 : Médical

Les chercheurs en médecine collectent souvent des données bivariées pour mieux comprendre la relation entre les variables liées à la santé.

Par exemple, un chercheur peut collecter les données suivantes sur l’âge et la fréquence cardiaque au repos de 15 personnes :

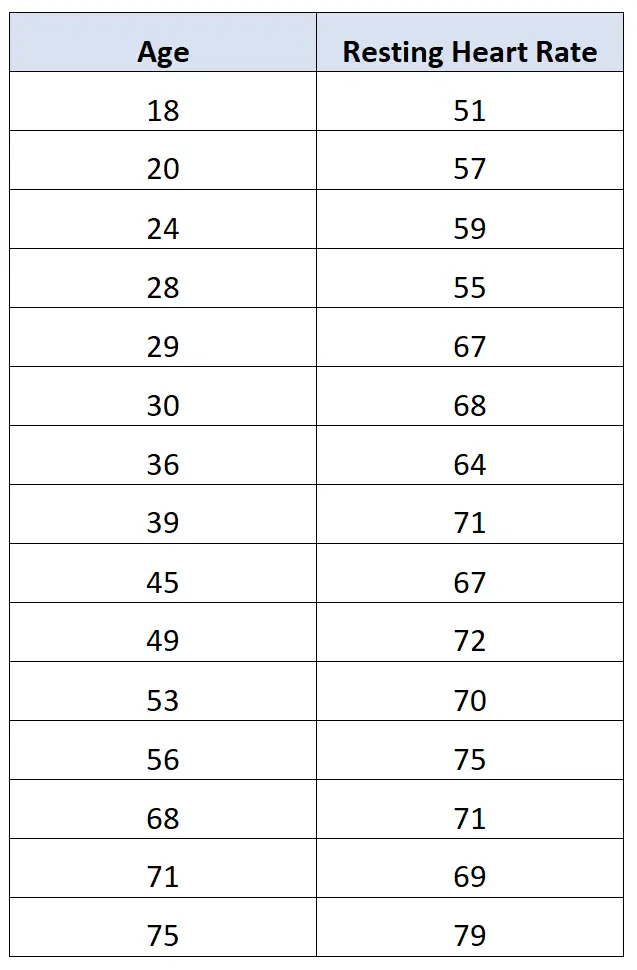
Le chercheur peut alors décider de calculer la corrélation entre les deux variables et la trouver égale à 0,812 .

Cela indique qu’il existe une forte corrélation positive entre les deux variables. Autrement dit, à mesure que l’âge augmente, la fréquence cardiaque au repos a également tendance à augmenter de manière prévisible.

Connexes :Qu’est-ce qui est considéré comme une corrélation « forte » ?

Exemple 3 : universitaires

Les chercheurs collectent souvent des données bivariées pour comprendre quelles variables affectent les performances des étudiants universitaires.

Par exemple, un chercheur peut collecter des données sur le nombre d’heures étudiées par semaine et la moyenne cumulative correspondante pour les étudiants d’une certaine classe :

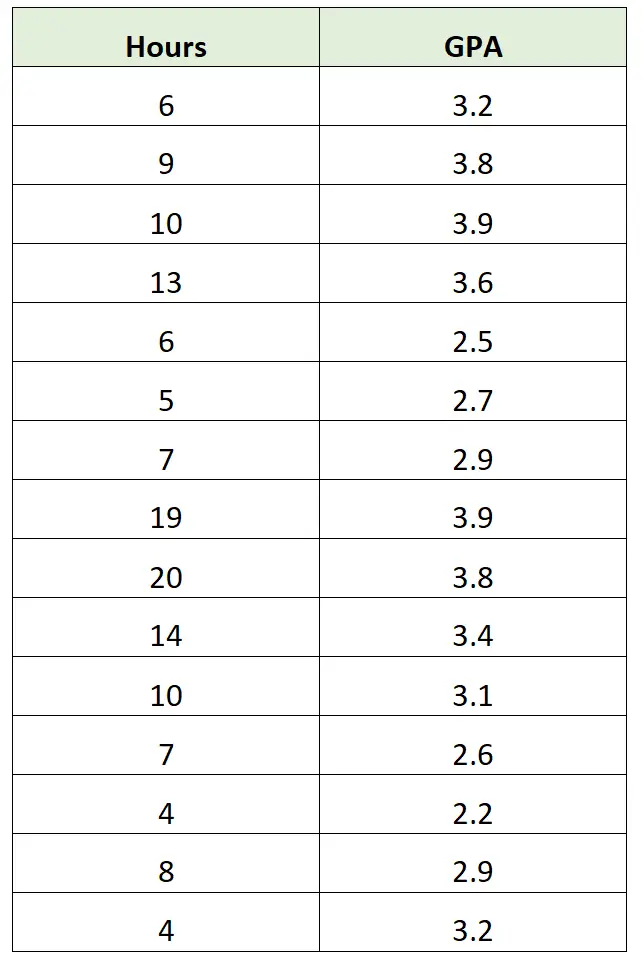
Elle peut ensuite créer un nuage de points simple pour visualiser la relation entre ces deux variables :

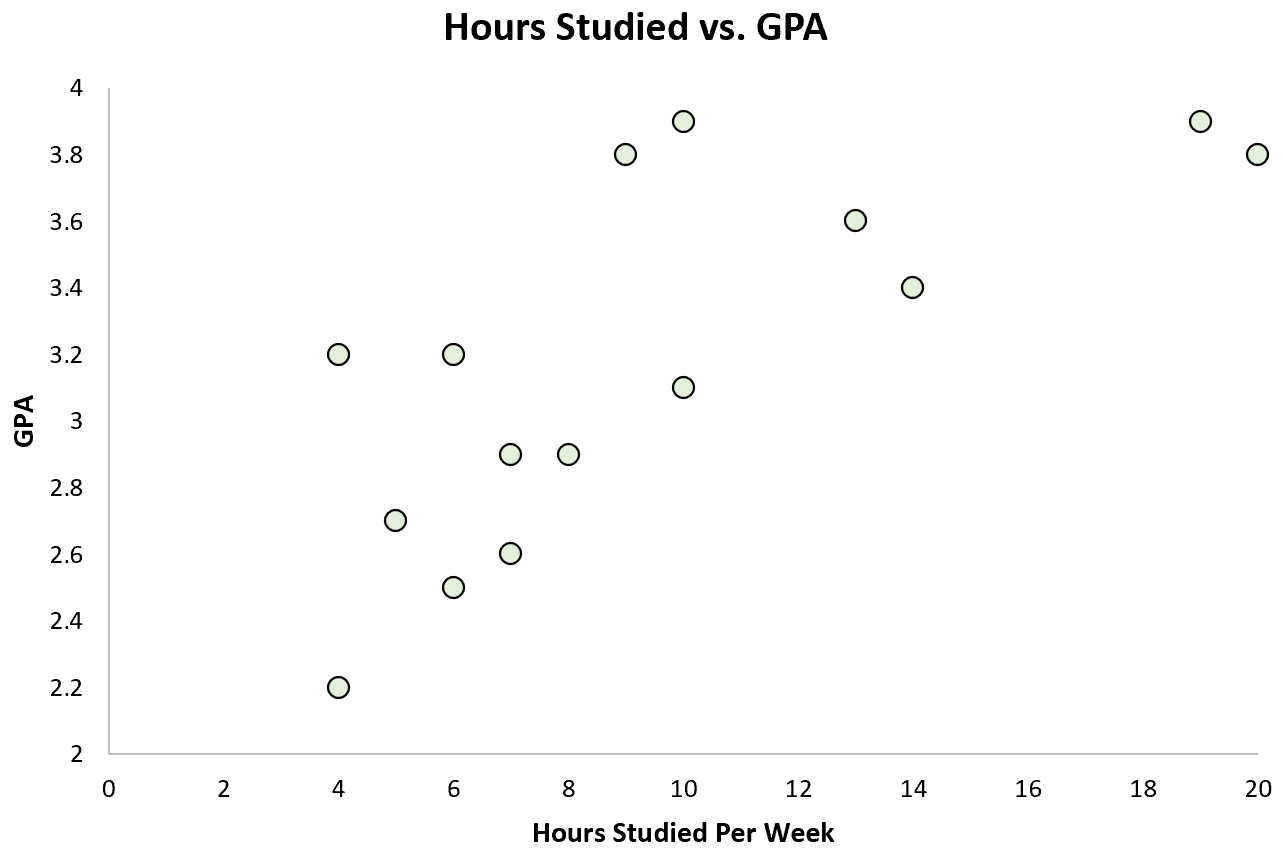
Il existe clairement une association positive entre les deux variables : à mesure que le nombre d’heures étudiées par semaine augmente, la moyenne générale de l’étudiant a également tendance à augmenter.

Exemple 4 : Économie

Les économistes collectent souvent des données bivariées pour comprendre la relation entre deux variables socio-économiques.

Par exemple, un économiste peut collecter des données sur le nombre total d’années de scolarité et le revenu annuel total des individus dans une certaine ville :

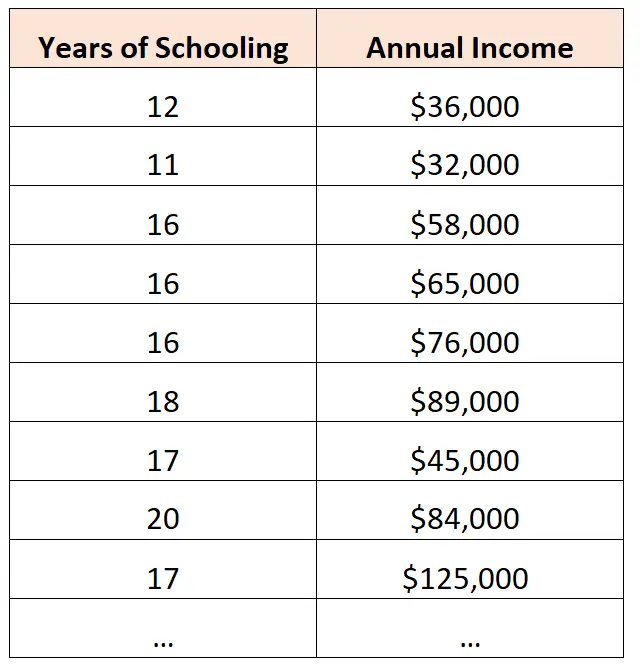
Il peut alors décider d’adapter le modèle de régression linéaire simple suivant :

Revenu annuel = -45 353 + 7 120*(Années de scolarité)

Cela indique à l’économiste que pour chaque année de scolarité supplémentaire, le revenu annuel augmente en moyenne de 7 120 $.

Exemple 5 : Biologie

Les biologistes collectent souvent des données bivariées pour comprendre comment deux variables sont liées entre les plantes ou les animaux.

Par exemple, un biologiste peut collecter des données sur les précipitations totales et le nombre total de plantes dans différentes régions :

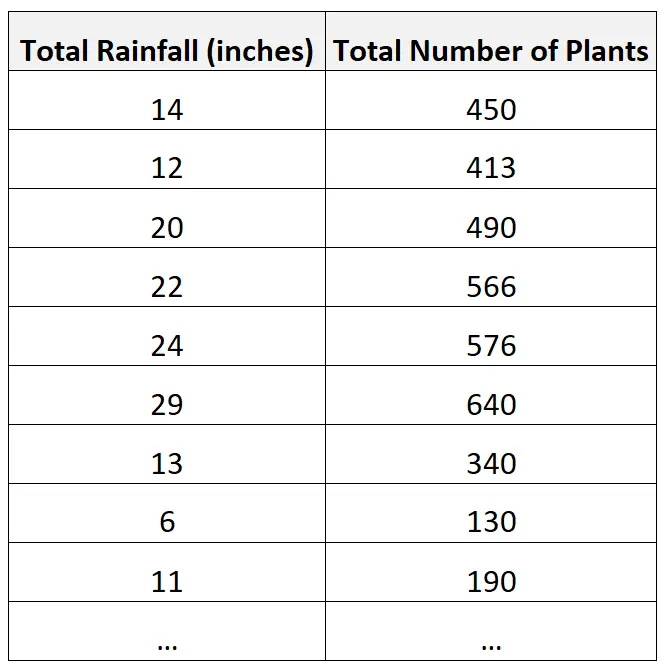
Le biologiste peut alors décider de calculer la corrélation entre les deux variables et la trouver égale à 0,926 .

Cela indique qu’il existe une forte corrélation positive entre les deux variables.

Autrement dit, des précipitations plus élevées sont étroitement associées à un nombre accru de plantes dans une région.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les données bivariées et sur la manière de les analyser.

Introduction à l’analyse bivariée
Introduction à l’analyse univariée
Introduction au coefficient de corrélation de Pearson
Introduction à la régression linéaire simple