Hétéroscédasticité

Cet article explique ce qu’est l’hétéroscédasticité dans les statistiques. De plus, vous découvrirez quelles sont les causes de l’hétéroscédasticité, quelles sont ses conséquences et comment y remédier.

Qu’est-ce que l’hétéroscédasticité ?

En statistique, l’hétéroscédasticité est une caractéristique qui présente un modèle de régression qui implique que la variance des erreurs n’est pas constante. Autrement dit, un modèle hétéroscédastique signifie que ses erreurs présentent une variance irrégulière, alors le modèle est dit hétéroscédastique.

Rappelons que l’erreur (ou résidu) est définie comme la différence entre la valeur réelle et la valeur estimée par le modèle de régression.

Lors de l’élaboration d’un modèle de régression, l’erreur commise par chaque observation est calculée à l’aide de l’expression précédente. Ainsi, un modèle statistique est hétéroscédastique lorsque la variance des erreurs calculées n’est pas constante tout au long des observations, mais varie plutôt.

Bien que cela puisse paraître très simple, il est important qu’un modèle de régression ne présente pas d’hétéroscédasticité, puisque le calcul du modèle est basé sur le fait que la variance des résidus est constante, en fait, c’est l’une des hypothèses précédentes de les modèles de régression.

Il existe certains tests statistiques qui permettent de détecter l’hétéroscédasticité, comme le test de White ou le test de Goldfeld-Quandt. Cependant, généralement en représentant graphiquement les résidus, leur hétéroscédasticité peut être identifiée.

Causes de l’hétéroscédasticité

Les causes les plus fréquentes d’hétéroscédasticité d’un modèle sont les suivantes :

• Lorsque la plage de données est très large par rapport à la moyenne. Si dans le même échantillon statistique il y a des valeurs très grandes et des valeurs très petites, il est probable que le modèle de régression obtenu soit hétéroscédastique.
• L’omission de variables dans le modèle de régression entraîne également une hétéroscédasticité. Logiquement, si une variable pertinente n’est pas incluse dans le modèle, sa variation sera incluse dans les résidus et celle-ci ne sera pas nécessairement fixe.
• De même, un changement dans la structure peut produire un mauvais ajustement du modèle à l’ensemble de données et, par conséquent, que la variance des résidus ne soit pas constante.
• Lorsque certaines variables ont des valeurs beaucoup plus grandes que les autres variables explicatives, le modèle peut avoir une hétéroscédasticité. Dans ce cas, les variables peuvent être relativisées pour résoudre le problème.

Cependant, certains cas sont, par nature, susceptibles de présenter une hétéroscédasticité. Par exemple, si nous modélisons le revenu d’une personne avec ses dépenses alimentaires, les personnes les plus riches ont une bien plus grande variabilité dans leurs dépenses alimentaires que les personnes les plus pauvres. Car une personne riche mange parfois dans des restaurants chers et d’autres fois dans des restaurants bon marché, contrairement à une personne pauvre qui mange toujours dans des restaurants bon marché. Par conséquent, il est facile pour le modèle de régression de posséder une hétéroscédasticité.

Conséquences de l’hétéroscédasticité

Principalement, les conséquences de l’hétéroscédasticité dans un modèle de régression sont les suivantes :

• L’efficacité est perdue dans l’estimateur des moindres carrés, défini comme la moyenne des carrés des erreurs.
• Des erreurs se produisent dans le calcul de la matrice de covariance des estimateurs des moindres carrés.

Hétéroscédasticité correcte

Lorsque le modèle de régression obtenu est hétéroscédastique, nous pouvons essayer les corrections suivantes pour obtenir l’hétéroscédasticité :

• Calculez le logarithme népérien de la variable indépendante, ceci est généralement utile lorsque la variance des résidus augmente dans le graphique.
• Selon le graphique des résidus, un autre type de transformation de la variable indépendante peut être plus pratique. Par exemple, si le graphique a la forme d’une parabole, nous pouvons calculer le carré de la variable indépendante et ajouter cette variable au modèle.
• D’autres variables peuvent également être utilisées pour le modèle ; en supprimant ou en ajoutant une variable, la variance des résidus peut être modifiée.
• Au lieu d’utiliser le critère des moindres carrés, le critère des moindres carrés pondérés peut être utilisé.

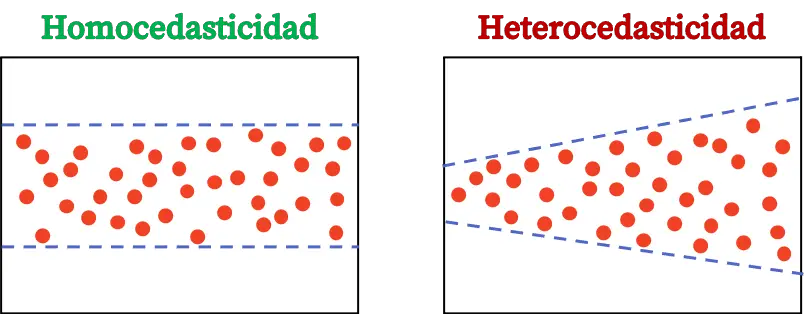
Hétéroscédasticité et homoscédasticité

Enfin, nous verrons quelles sont les différences entre hétéroscédasticité et homoscédasticité en statistique, puisque ce sont deux concepts de modèles de régression sur lesquels il faut être clair.

L’ homoscédasticité d’un modèle de régression est une caractéristique statistique qui indique que la variance des erreurs est constante. Ainsi, un modèle homoscédastique signifie que la variance de ses erreurs est constante.

La différence entre hétéroscédasticité et homoscédasticité se retrouve dans la constance de la variance des résidus. Si la variance des résidus d’un modèle n’est pas constante, cela signifie que le modèle est hétéroscédastique. En revanche, si la variance des résidus est constante, cela signifie qu’elle est homoscédastique.

Par conséquent, nous devons nous assurer que le modèle de régression que nous construisons est homoscédastique, de cette manière l’hypothèse selon laquelle la variance des résidus est constante sera remplie.