Comment créer un histogramme de résidus dans R

L’une des principales hypothèses de la régression linéaire est que les résidus sont normalement distribués.

Une façon de vérifier visuellement cette hypothèse consiste à créer un histogramme des résidus et à observer si la distribution suit ou non une « forme de cloche » rappelant la distribution normale .

Ce didacticiel fournit un exemple étape par étape de la façon de créer un histogramme de résidus pour un modèle de régression dans R.

Étape 1 : Créer les données

Tout d’abord, créons de fausses données avec lesquelles travailler :

#make this example reproducible
set.seed(0)

#create data
x1 <- rnorm(n=100, 2, 1)
x2 <- rnorm(100, 4, 3)
y  <- rnorm(100, 2, 3)
data <- data.frame(x1, x2, y)

#view first six rows of data
head(data)

        x1        x2          y
1 3.262954 6.3455776 -1.1371530
2 1.673767 1.6696701 -0.6886338
3 3.329799 2.1520303  5.8081615
4 3.272429 4.1397409  3.7815228
5 2.414641 0.6088427  4.3269030
6 0.460050 5.7301563  6.6721111

Étape 2 : Ajuster le modèle de régression

Ensuite, nous adapterons un modèle de régression linéaire multiple aux données :

#fit multiple linear regression model
model <- lm(y ~ x1 + x2, data=data)

Étape 3 : Créer un histogramme des résidus

Enfin, nous utiliserons le package de visualisation ggplot pour créer un histogramme des résidus du modèle :

#load ggplot2
library(ggplot2)

#create histogram of residuals
ggplot(data = data, aes(x = model$residuals)) +
    geom_histogram(fill = 'steelblue', color = 'black') +
    labs(title = 'Histogram of Residuals', x = 'Residuals', y = 'Frequency')

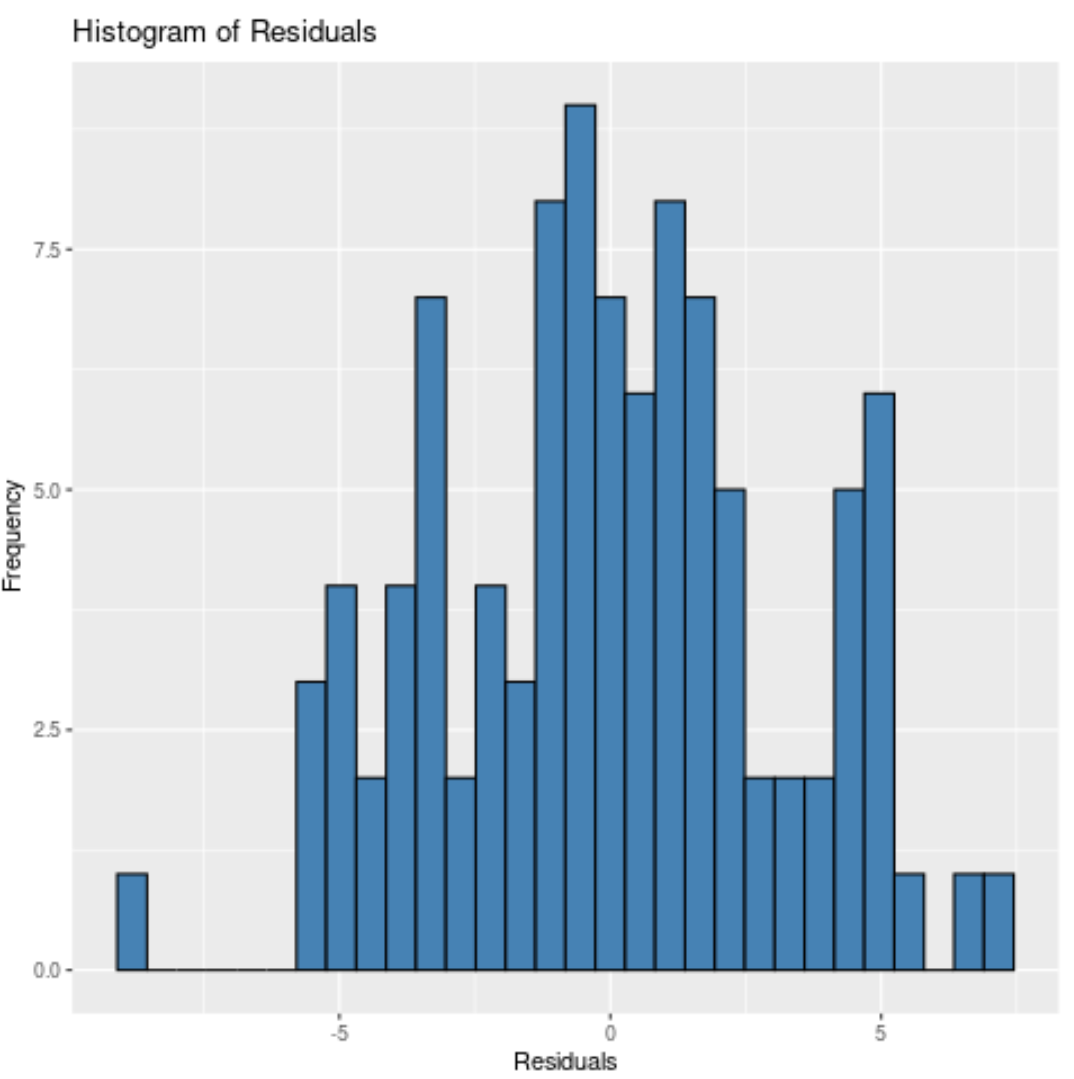
Notez que nous pouvons également spécifier le nombre de compartiments dans lesquels placer les résidus en utilisant l’argument bin .

Moins il y a de cases, plus les barres seront larges dans l’histogramme. Par exemple, nous pourrions spécifier 20 bins :

#create histogram of residuals
ggplot(data = data, aes(x = model$residuals)) +
    geom_histogram(bins = 20, fill = 'steelblue', color = 'black') +
    labs(title = 'Histogram of Residuals', x = 'Residuals', y = 'Frequency')

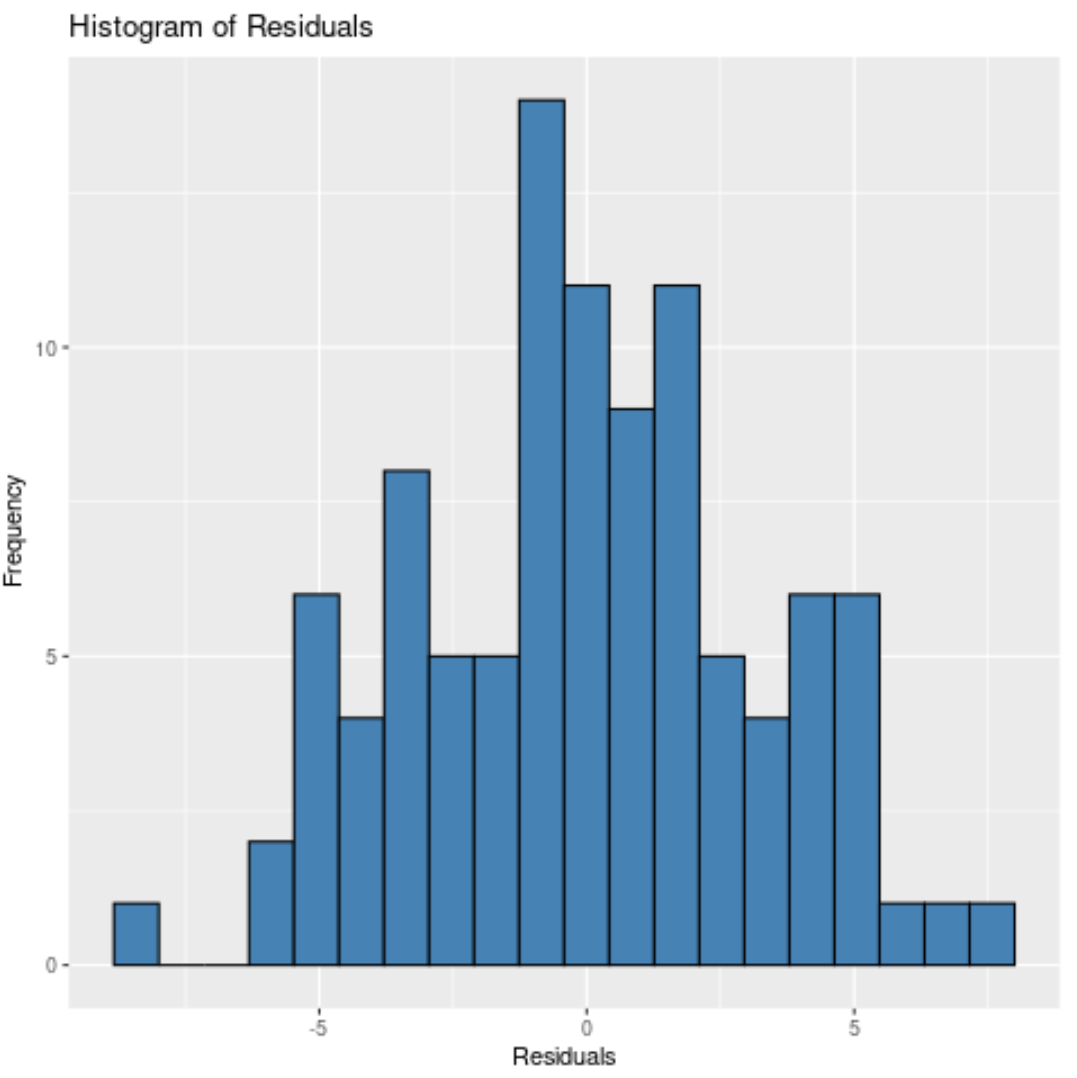
Ou nous pourrions spécifier 10 bacs :

#create histogram of residuals
ggplot(data = data, aes(x = model$residuals)) +
    geom_histogram(bins = 10, fill = 'steelblue', color = 'black') +
    labs(title = 'Histogram of Residuals', x = 'Residuals', y = 'Frequency')

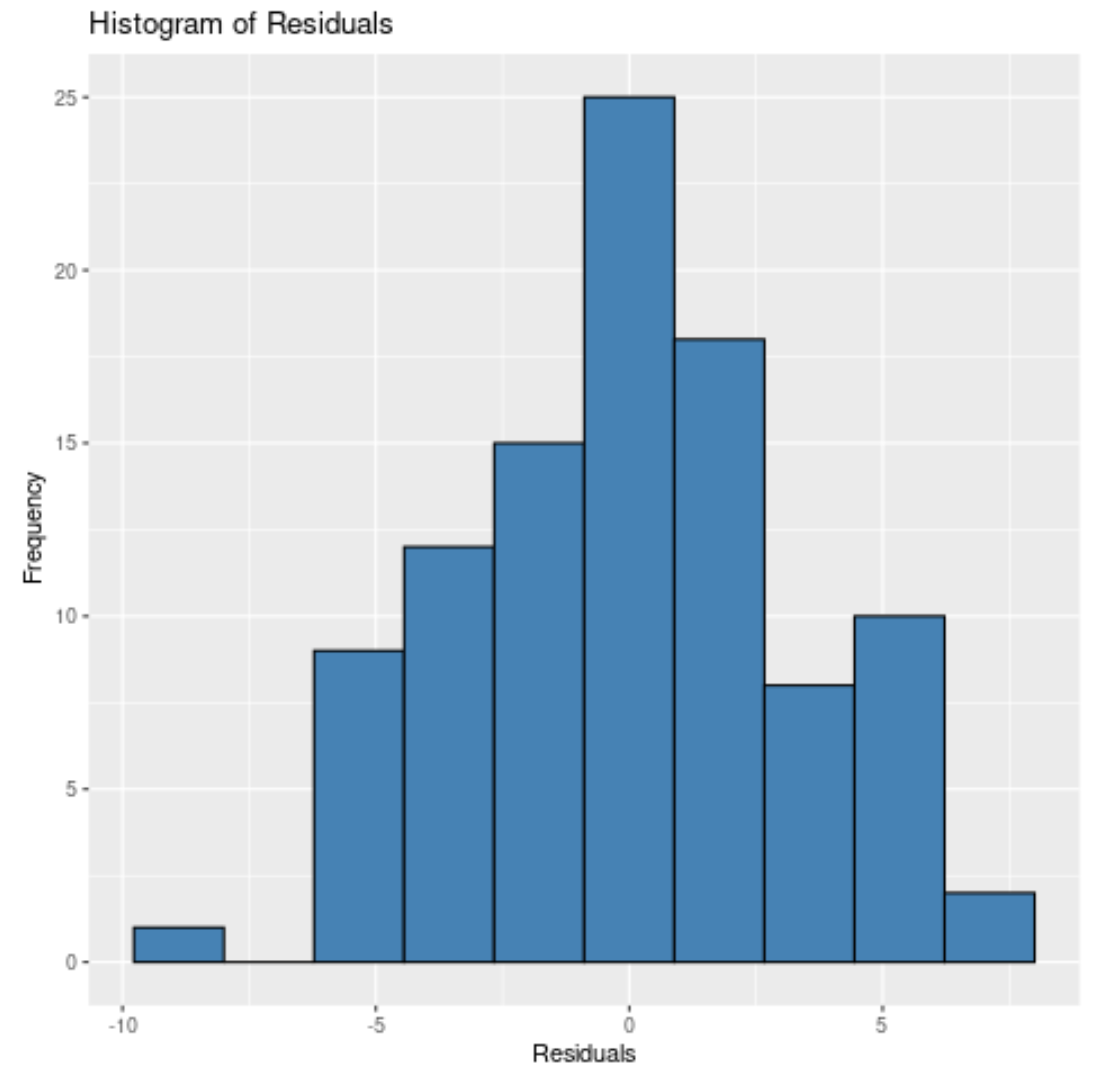
Quel que soit le nombre de cases que nous spécifions, nous pouvons voir que les résidus sont à peu près normalement distribués.

Nous pourrions également effectuer un test statistique formel comme Shapiro-Wilk, Kolmogorov-Smirnov ou Jarque-Bera pour tester la normalité.

Cependant, gardez à l’esprit que ces tests sont sensibles aux échantillons de grande taille – c’est-à-dire qu’ils concluent souvent que les résidus ne sont pas normaux lorsque la taille de l’échantillon est grande.

Pour cette raison, il est souvent plus facile d’évaluer la normalité en créant un histogramme des résidus.