Comprendre l’hypothèse nulle pour les modèles ANOVA

Une ANOVA unidirectionnelle est utilisée pour déterminer s’il existe une différence statistiquement significative entre la moyenne de trois groupes indépendants ou plus.

Une ANOVA unidirectionnelle utilise les hypothèses nulles et alternatives suivantes :

• H ₀ : μ ₁ = μ ₂ = μ ₃ = … = μ _k (toutes les moyennes du groupe sont égales)
• H _A : Au moins une moyenne de groupe est différente   du reste

Pour décider si nous devons rejeter ou non l’hypothèse nulle, nous devons nous référer à la valeur p dans le résultat du tableau ANOVA.

Si la valeur p est inférieure à un certain niveau de signification (par exemple 0,05), nous pouvons alors rejeter l’hypothèse nulle et conclure que toutes les moyennes des groupes ne sont pas égales.

Une ANOVA bidirectionnelle est utilisée pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes indépendants ou plus qui ont été répartis sur deux variables (parfois appelées « facteurs »).

Une ANOVA bidirectionnelle teste trois hypothèses nulles en même temps :

• Toutes les moyennes de groupe sont égales à chaque niveau de la première variable
• Toutes les moyennes de groupe sont égales à chaque niveau de la deuxième variable
• Il n’y a pas d’effet d’interaction entre les deux variables

Pour décider si nous devons rejeter ou non chaque hypothèse nulle, nous devons nous référer aux valeurs p dans le résultat du tableau ANOVA bidirectionnel.

Les exemples suivants montrent comment décider de rejeter ou de ne pas rejeter l’hypothèse nulle dans une ANOVA unidirectionnelle et une ANOVA bidirectionnelle.

Exemple 1 : ANOVA unidirectionnelle

Supposons que nous voulions savoir si trois programmes de préparation aux examens différents conduisent ou non à des notes moyennes différentes à un examen donné. Pour tester cela, nous recrutons 30 étudiants pour participer à une étude et les répartissons en trois groupes.

Les étudiants de chaque groupe sont assignés au hasard à utiliser l’un des trois programmes de préparation aux examens pendant les trois semaines suivantes pour se préparer à un examen. A la fin des trois semaines, tous les étudiants passent le même examen.

Les résultats des examens pour chaque groupe sont indiqués ci-dessous :

Lorsque nous entrons ces valeurs dans le calculateur d’ANOVA unidirectionnel , nous recevons le tableau ANOVA suivant en sortie :

Notez que la valeur p est 0,11385 .

Pour cet exemple particulier, nous utiliserions les hypothèses nulles et alternatives suivantes :

• H ₀ : μ ₁ = μ ₂ = μ ₃ (la note moyenne à l’examen pour chaque groupe est égale)
• H _A : Au moins une moyenne de groupe est différente   du reste

Étant donné que la valeur p du tableau ANOVA n’est pas inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle.

Cela signifie que nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une différence statistiquement significative entre les résultats moyens aux examens des trois groupes.

Exemple 2 : ANOVA bidirectionnelle

Supposons qu’un botaniste veuille savoir si la croissance des plantes est influencée par l’exposition au soleil et la fréquence des arrosages.

Elle plante 40 graines et les laisse pousser pendant deux mois dans différentes conditions d’exposition au soleil et de fréquence d’arrosage. Au bout de deux mois, elle enregistre la hauteur de chaque plante. Les résultats sont montrés plus bas:

Dans le tableau ci-dessus, nous voyons que cinq plantes ont été cultivées dans chaque combinaison de conditions.

Par exemple, cinq plantes ont été cultivées avec un arrosage quotidien et sans lumière du soleil et leurs hauteurs après deux mois étaient de 4,8 pouces, 4,4 pouces, 3,2 pouces, 3,9 pouces et 4,4 pouces :

Elle effectue une ANOVA bidirectionnelle dans Excel et obtient le résultat suivant :

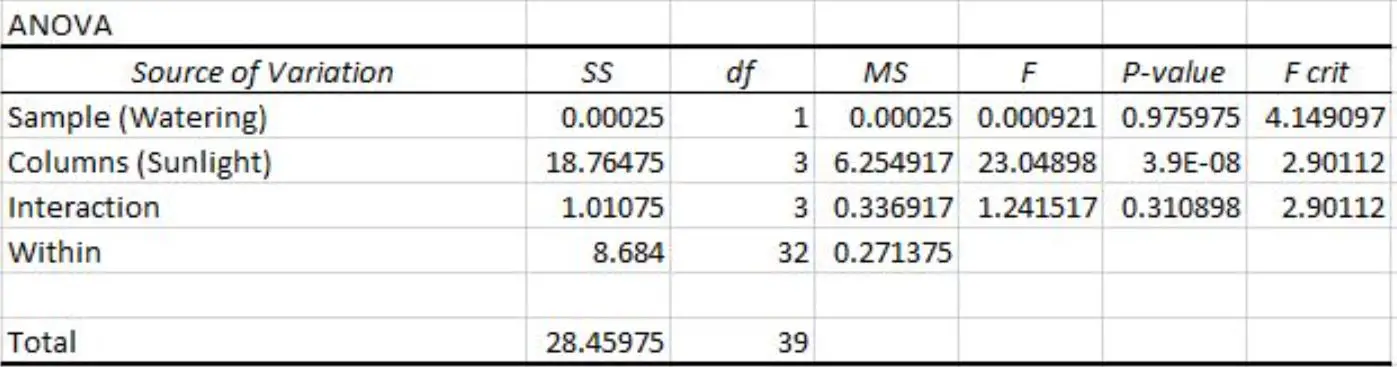
Nous pouvons voir les valeurs p suivantes dans le résultat du tableau ANOVA bidirectionnel :

• La valeur p pour la fréquence d’arrosage est de 0,975975 . Ceci n’est pas statistiquement significatif au niveau de signification de 0,05.
• La valeur p pour l’exposition au soleil est de 3,9E-8 (0,000000039) . Ceci est statistiquement significatif au niveau de signification de 0,05.
• La valeur p pour l’interaction entre la fréquence d’arrosage et l’exposition au soleil est de 0,310898 . Ceci n’est pas statistiquement significatif au niveau de signification de 0,05.

Ces résultats indiquent que l’exposition au soleil est le seul facteur ayant un effet statistiquement significatif sur la hauteur des plantes.

Et comme il n’y a pas d’effet d’interaction, l’effet de l’exposition au soleil est cohérent à chaque niveau de fréquence d’arrosage.

Autrement dit, le fait qu’une plante soit arrosée quotidiennement ou hebdomadairement n’a aucun impact sur la façon dont l’exposition au soleil affecte une plante.

Ressources additionnelles

Les didacticiels suivants fournissent des informations supplémentaires sur les modèles ANOVA :

Comment interpréter la valeur F et la valeur P dans l’ANOVA
Comment calculer la somme des carrés en ANOVA
Que signifie une valeur F élevée dans l’ANOVA ?