Les cinq hypothèses de la régression linéaire multiple
La régression linéaire multiple est une méthode statistique que nous pouvons utiliser pour comprendre la relation entre plusieurs variables prédictives et une variable de réponse .
Cependant, avant d’effectuer une régression linéaire multiple, nous devons d’abord nous assurer que cinq hypothèses sont remplies :
1. Relation linéaire : Il existe une relation linéaire entre chaque variable prédictive et la variable de réponse.
2. Pas de multicolinéarité : aucune des variables prédictives n’est fortement corrélée les unes aux autres.
3. Indépendance : Les observations sont indépendantes.
4. Homoscédasticité : les résidus ont une variance constante en chaque point du modèle linéaire.
5. Normalité multivariée : Les résidus du modèle sont normalement distribués.
Si une ou plusieurs de ces hypothèses ne sont pas respectées, les résultats de la régression linéaire multiple peuvent alors ne pas être fiables.
Dans cet article, nous fournissons une explication pour chaque hypothèse, comment déterminer si l’hypothèse est satisfaite et que faire si l’hypothèse n’est pas respectée.
Hypothèse 1 : Relation linéaire
La régression linéaire multiple suppose qu’il existe une relation linéaire entre chaque variable prédictive et la variable de réponse.
Comment déterminer si cette hypothèse est remplie
Le moyen le plus simple de déterminer si cette hypothèse est satisfaite est de créer un nuage de points de chaque variable prédictive et de la variable de réponse.
Cela vous permet de voir visuellement s’il existe une relation linéaire entre les deux variables.
Si les points du nuage de points se situent à peu près le long d’une ligne diagonale droite, il existe probablement une relation linéaire entre les variables.
Par exemple, les points du graphique ci-dessous semblent tomber sur une ligne droite, ce qui indique qu’il existe une relation linéaire entre cette variable prédictive particulière (x) et la variable de réponse (y) :
Que faire si cette hypothèse n’est pas respectée
S’il n’y a pas de relation linéaire entre une ou plusieurs variables prédictives et la variable de réponse, nous avons alors plusieurs options :
1. Appliquez une transformation non linéaire à la variable prédictive, par exemple en prenant le log ou la racine carrée. Cela peut souvent transformer la relation en une relation plus linéaire.
2. Ajoutez une autre variable prédictive au modèle. Par exemple, si le tracé de x en fonction de y a une forme parabolique, il peut être judicieux d’ajouter X 2 comme variable prédictive supplémentaire dans le modèle.
3. Supprimez la variable prédictive du modèle. Dans le cas le plus extrême, s’il n’existe aucune relation linéaire entre une certaine variable prédictive et la variable de réponse, il peut alors ne pas être utile d’inclure la variable prédictive dans le modèle.
Hypothèse 2 : pas de multicolinéarité
La régression linéaire multiple suppose qu’aucune des variables prédictives n’est fortement corrélée entre elles.
Lorsqu’une ou plusieurs variables prédictives sont fortement corrélées, le modèle de régression souffre de multicolinéarité , ce qui rend les estimations des coefficients du modèle peu fiables.
Comment déterminer si cette hypothèse est remplie
Le moyen le plus simple de déterminer si cette hypothèse est remplie est de calculer la valeur VIF pour chaque variable prédictive.
Les valeurs VIF commencent à 1 et n’ont pas de limite supérieure. En règle générale, les valeurs VIF supérieures à 5* indiquent une multicolinéarité potentielle.
Les tutoriels suivants montrent comment calculer le VIF dans divers logiciels statistiques :
* Parfois, les chercheurs utilisent plutôt une valeur VIF de 10, selon le domaine d’études.
Que faire si cette hypothèse n’est pas respectée
Si une ou plusieurs variables prédictives ont une valeur VIF supérieure à 5, le moyen le plus simple de résoudre ce problème consiste simplement à supprimer la ou les variables prédictives ayant les valeurs VIF élevées.
Alternativement, si vous souhaitez conserver chaque variable prédictive dans le modèle, vous pouvez utiliser une méthode statistique différente, telle que la régression de crête , la régression au lasso ou la régression des moindres carrés partiels , conçue pour gérer les variables prédictives hautement corrélées.
Hypothèse 3 : Indépendance
La régression linéaire multiple suppose que chaque observation de l’ensemble de données est indépendante.
Comment déterminer si cette hypothèse est remplie
Le moyen le plus simple de déterminer si cette hypothèse est satisfaite est d’effectuer un test de Durbin-Watson , qui est un test statistique formel qui nous indique si les résidus (et donc les observations) présentent ou non une autocorrélation.
Que faire si cette hypothèse n’est pas respectée
Selon la manière dont cette hypothèse est violée, vous disposez de plusieurs options :
- Pour une corrélation en série positive, envisagez d’ajouter des décalages de la variable dépendante et/ou indépendante au modèle.
- Pour une corrélation série négative, assurez-vous qu’aucune de vos variables n’est surdifférée .
- Pour la corrélation saisonnière, envisagez d’ajouter des variables fictives saisonnières au modèle.
Hypothèse 4 : homoscédasticité
La régression linéaire multiple suppose que les résidus ont une variance constante en chaque point du modèle linéaire. Lorsque ce n’est pas le cas, les résidus souffrent d’ hétéroscédasticité .
Lorsque l’hétéroscédasticité est présente dans une analyse de régression, les résultats du modèle de régression deviennent peu fiables.
Plus précisément, l’hétéroscédasticité augmente la variance des estimations du coefficient de régression, mais le modèle de régression n’en tient pas compte. Cela rend beaucoup plus probable qu’un modèle de régression déclare qu’un terme du modèle est statistiquement significatif, alors qu’en réalité il ne l’est pas.
Comment déterminer si cette hypothèse est remplie
Le moyen le plus simple de déterminer si cette hypothèse est respectée consiste à créer un graphique des résidus standardisés par rapport aux valeurs prédites.
Une fois que vous avez ajusté un modèle de régression à un ensemble de données, vous pouvez créer un nuage de points qui affiche les valeurs prédites de la variable de réponse sur l’axe des x et les résidus standardisés du modèle sur l’axe des y.
Si les points du nuage de points présentent une tendance, alors l’hétéroscédasticité est présente.
Le graphique suivant montre un exemple de modèle de régression dans lequel l’hétéroscédasticité ne pose pas de problème :
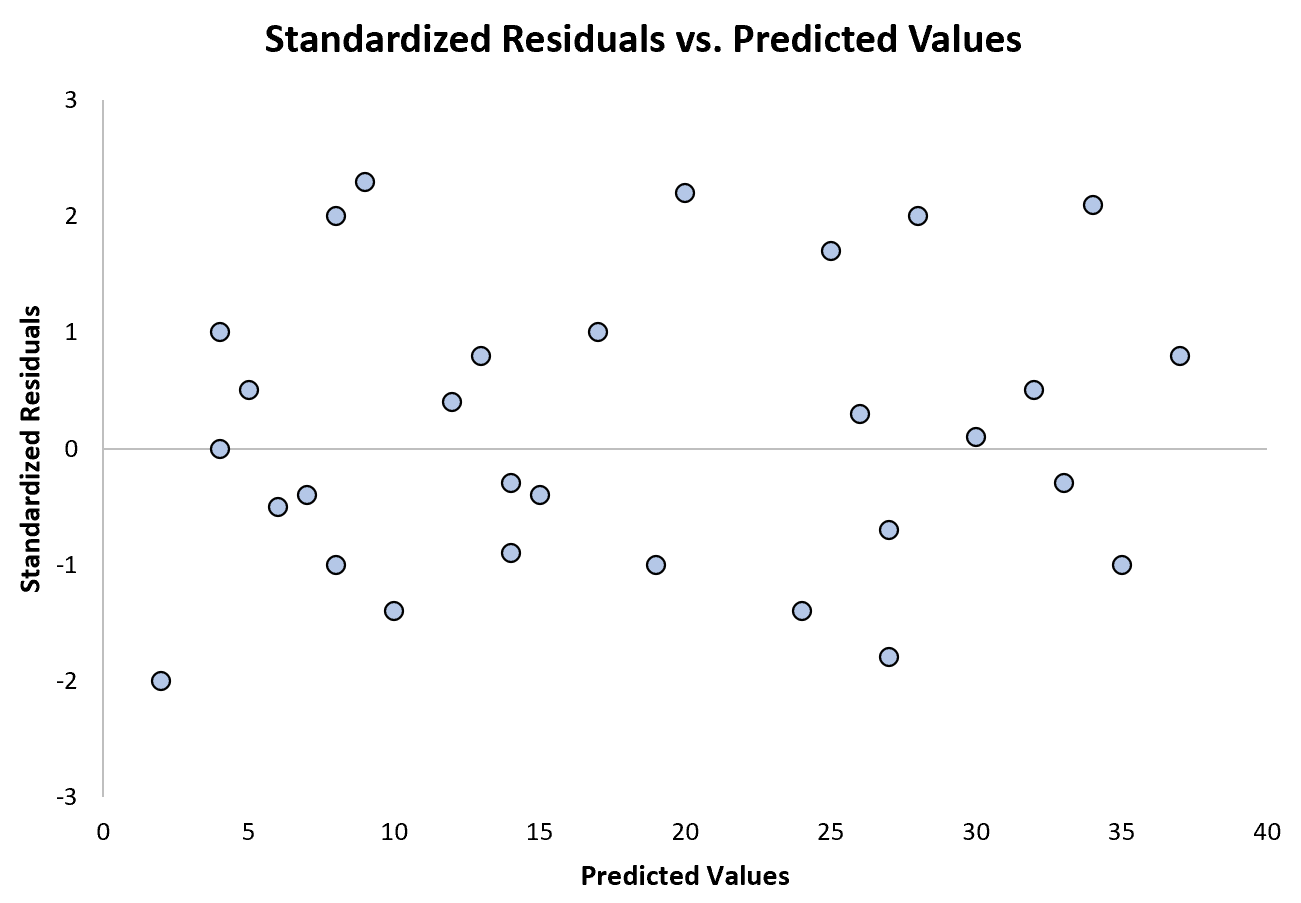
Notez que les résidus standardisés sont dispersés autour de zéro sans motif clair.
Le graphique suivant montre un exemple de modèle de régression dans lequel l’hétéroscédasticité pose problème :
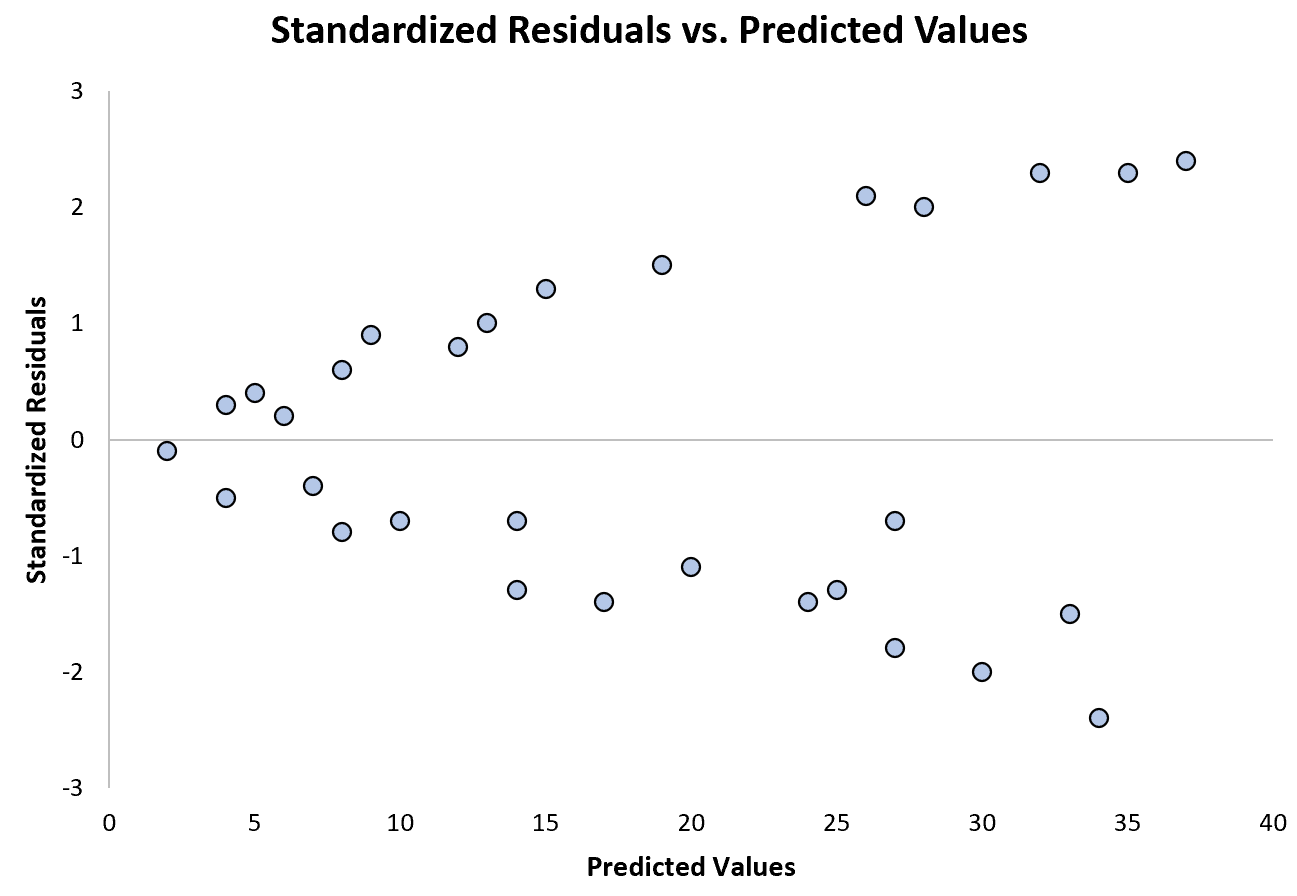
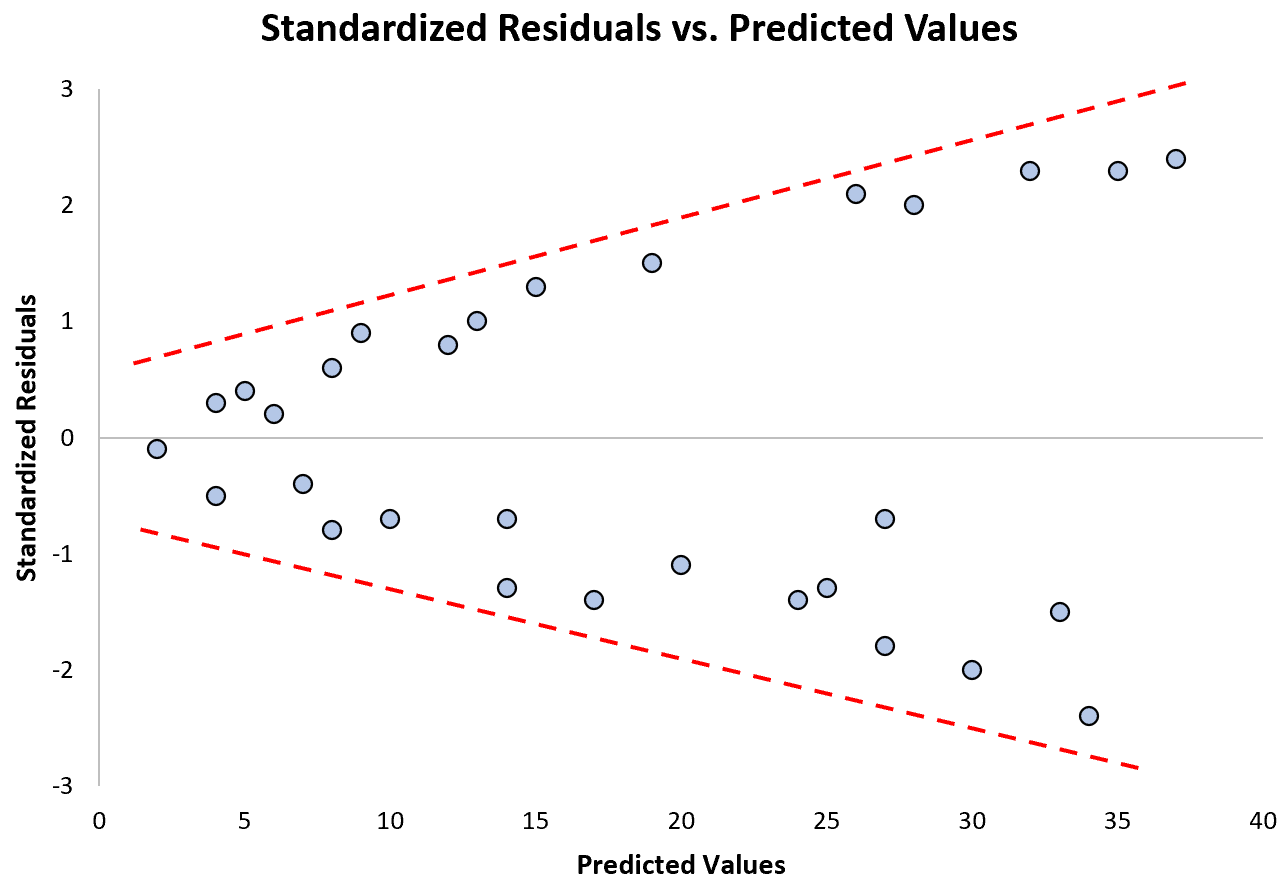
Remarquez comment les résidus standardisés s’étalent de plus en plus à mesure que les valeurs prédites augmentent. Cette forme de « cône » est un signe classique d’hétéroscédasticité :
Que faire si cette hypothèse n’est pas respectée
Il existe trois manières courantes de corriger l’hétéroscédasticité :
1. Transformez la variable de réponse. La manière la plus courante de traiter l’hétéroscédasticité consiste à transformer la variable de réponse en prenant le log, la racine carrée ou la racine cubique de toutes les valeurs de la variable de réponse. Cela entraîne souvent la disparition de l’hétéroscédasticité.
2. Redéfinissez la variable de réponse. Une façon de redéfinir la variable de réponse consiste à utiliser un taux plutôt que la valeur brute. Par exemple, au lieu d’utiliser la taille de la population pour prédire le nombre de fleuristes dans une ville, nous pouvons utiliser la taille de la population pour prédire le nombre de fleuristes par habitant.
Dans la plupart des cas, cela réduit la variabilité qui se produit naturellement au sein de populations plus importantes puisque nous mesurons le nombre de fleuristes par personne, plutôt que le nombre même de fleuristes.
3. Utilisez la régression pondérée. Une autre façon de corriger l’hétéroscédasticité consiste à utiliser la régression pondérée, qui attribue un poids à chaque point de données en fonction de la variance de sa valeur ajustée.
Essentiellement, cela donne de faibles poids aux points de données qui ont des variances plus élevées, ce qui réduit leurs carrés résiduels. Lorsque les pondérations appropriées sont utilisées, cela peut éliminer le problème de l’hétéroscédasticité.
Connexe : Comment effectuer une régression pondérée dans R
Hypothèse 4 : Normalité multivariée
La régression linéaire multiple suppose que les résidus du modèle sont normalement distribués.
Comment déterminer si cette hypothèse est remplie
Il existe deux manières courantes de vérifier si cette hypothèse est satisfaite :
1. Vérifiez visuellement l’hypothèse à l’aide des tracés QQ .
Un tracé QQ, abréviation de quantile-quantile plot, est un type de tracé que nous pouvons utiliser pour déterminer si les résidus d’un modèle suivent ou non une distribution normale. Si les points du tracé forment à peu près une ligne diagonale droite, alors l’hypothèse de normalité est remplie.
Le tracé QQ suivant montre un exemple de résidus qui suivent à peu près une distribution normale :
Cependant, le graphique QQ ci-dessous montre un exemple de cas où les résidus s’écartent clairement d’une ligne diagonale droite, ce qui indique qu’ils ne suivent pas la distribution normale :
2. Vérifiez l’hypothèse à l’aide d’un test statistique formel comme Shapiro-Wilk, Kolmogorov-Smironov, Jarque-Barre ou D’Agostino-Pearson.
Gardez à l’esprit que ces tests sont sensibles aux échantillons de grande taille – c’est-à-dire qu’ils concluent souvent que les résidus ne sont pas normaux lorsque la taille de votre échantillon est extrêmement grande. C’est pourquoi il est souvent plus facile d’utiliser des méthodes graphiques comme un tracé QQ pour vérifier cette hypothèse.
Que faire si cette hypothèse n’est pas respectée
Si l’hypothèse de normalité n’est pas respectée, vous disposez de plusieurs options :
1. Tout d’abord, vérifiez qu’il n’y a pas de valeurs aberrantes extrêmes présentes dans les données qui entraînent une violation de l’hypothèse de normalité.
2. Ensuite, vous pouvez appliquer une transformation non linéaire à la variable de réponse, par exemple en prenant la racine carrée, le log ou la racine cubique de toutes les valeurs de la variable de réponse. Cela entraîne souvent une distribution plus normale des résidus du modèle.
Ressources additionnelles
Les didacticiels suivants fournissent des informations supplémentaires sur la régression linéaire multiple et ses hypothèses :
Introduction à la régression linéaire multiple
Un guide sur l’hétéroscédasticité dans l’analyse de régression
Un guide sur la multicolinéarité et le VIF en régression
Les didacticiels suivants fournissent des exemples étape par étape sur la manière d’effectuer une régression linéaire multiple à l’aide de différents logiciels statistiques :
Comment effectuer une régression linéaire multiple dans Excel
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression linéaire multiple dans SPSS
Comment effectuer une régression linéaire multiple dans Stata
à propos de l'auteur
Dr. Benjamin Anderson
Il est un professeur de statistiques à la retraite devenu éducateur dévoué sur Statorials. Avec une vaste expérience et une expertise dans le domaine des statistiques, je m'engage à partager mes connaissances pour responsabiliser les étudiants grâce à Statorials. Lire plus