Intervalle de confiance pour la proportion
Cet article explique ce qu’est l’intervalle de confiance pour la proportion et à quoi il sert dans les statistiques. De même, vous découvrirez comment calculer l’intervalle de confiance de la proportion ainsi qu’un exercice résolu pour mieux comprendre le concept.
Quel est l’intervalle de confiance de la proportion ?
L’ intervalle de confiance pour la proportion est un intervalle qui fournit une plage de valeurs admissibles pour la proportion d’une population. Autrement dit, l’intervalle de confiance pour la proportion indique une valeur maximale et une valeur minimale entre lesquelles se situe la proportion de population avec une marge d’erreur.
Par exemple, si l’intervalle de confiance pour la proportion d’une population avec un niveau de confiance de 95 % est (0,73, 0,81), cela signifie que la proportion d’une population est comprise entre 73 % et 81 % avec une probabilité de 95 %.
Par conséquent, l’intervalle de confiance de la proportion est utilisé pour estimer la valeur de la proportion d’une population qui répond à certaines caractéristiques.
Comme nous le verrons dans la section suivante, l’intervalle de confiance pour la proportion dépend de la proportion de l’échantillon et du nombre d’observations dans l’échantillon.
Formule d’intervalle de confiance pour la proportion
L’intervalle de confiance pour la proportion est calculé en ajoutant et en soustrayant de la proportion de l’échantillon la valeur de Z α/2 multipliée par la racine carrée de la proportion de l’échantillon (p) multipliée par 1-p et divisée par la taille de l’échantillon ( n). Par conséquent, la formule pour calculer l’intervalle de confiance pour la proportion est la suivante :

Où:
 est la proportion de l’échantillon.
est la proportion de l’échantillon. est la taille de l’échantillon.
est la taille de l’échantillon. est le quantile de la distribution normale standard correspondant à une probabilité de α/2. Pour des échantillons de grande taille et un niveau de confiance de 95 %, il est généralement proche de 1,96 et pour un niveau de confiance de 99 %, il est généralement proche de 2,576.
est le quantile de la distribution normale standard correspondant à une probabilité de α/2. Pour des échantillons de grande taille et un niveau de confiance de 95 %, il est généralement proche de 1,96 et pour un niveau de confiance de 99 %, il est généralement proche de 2,576.
Exemple de calcul d’un intervalle de confiance pour la proportion
Afin que vous puissiez voir comment un intervalle de confiance pour la proportion est calculé, nous vous laissons ci-dessous un exemple concret étape par étape.
- Une compagnie d’assurance souhaite réaliser une étude de marché et déterminer combien de personnes dans un pays disposent d’une assurance-vie. Pour ce faire, un échantillon aléatoire de 700 personnes est analysé et on arrive à la conclusion que 40 % de l’échantillon dispose d’une assurance vie. Quel est l’intervalle de confiance au niveau de confiance de 95 % pour la proportion de la population du pays ?
Pour déterminer l’intervalle de confiance de la proportion de population, nous devons utiliser la formule que nous avons vue ci-dessus :

Dans ce cas, nous voulons que le niveau de confiance de l’intervalle de confiance soit de 95 %, donc la valeur de Z α/2 que nous devons prendre est de 1,96.
![]()
![Rendered by QuickLaTeX.com \begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}](https://statorials.org/wp-content/ql-cache/quicklatex.com-54dda39d0da5b29f2d25728b89565859_l3.png)
L’énoncé du problème nous indique déjà que la taille de l’échantillon est n=700 et que la proportion observée dans l’échantillon est p=0,40, nous substituons donc les données dans la formule de l’intervalle de confiance pour la proportion et calculons les limites de l’intervalle :

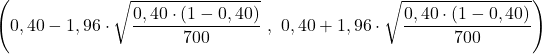
![]()
En conclusion, la proportion de la population étudiée se situe entre 36% et 44% avec un niveau de confiance de 95%.
