Comment effectuer un test de Kruskal-Wallis dans Stata

Un test de Kruskal-Wallis est utilisé pour déterminer s’il existe ou non une différence statistiquement significative entre les médianes de trois groupes indépendants ou plus. Elle est considérée comme l’équivalent non paramétrique de l’ ANOVA unidirectionnelle .

Ce didacticiel explique comment effectuer un test de Kruskal-Wallis dans Stata.

Comment effectuer un test de Kruskal-Wallis dans Stata

Pour cet exemple, nous utiliserons l’ensemble de données du recensement , qui contient les données du recensement de 1980 pour les cinquante États des États-Unis. Dans l’ensemble de données, les États sont classés en quatre régions différentes :

• Nord-est
• Centre-Nord
• Sud
• Ouest

Nous effectuerons un test de Kruskal-Wallis pour déterminer si l’âge médian est égal dans ces quatre régions.

Étape 1 : Chargez et affichez les données.

Tout d’abord, chargez l’ensemble de données en tapant la commande suivante dans la zone Commande :

utilisez https://www.stata-press.com/data/r13/census

Obtenez un résumé rapide de l’ensemble de données à l’aide de la commande suivante :

résumer

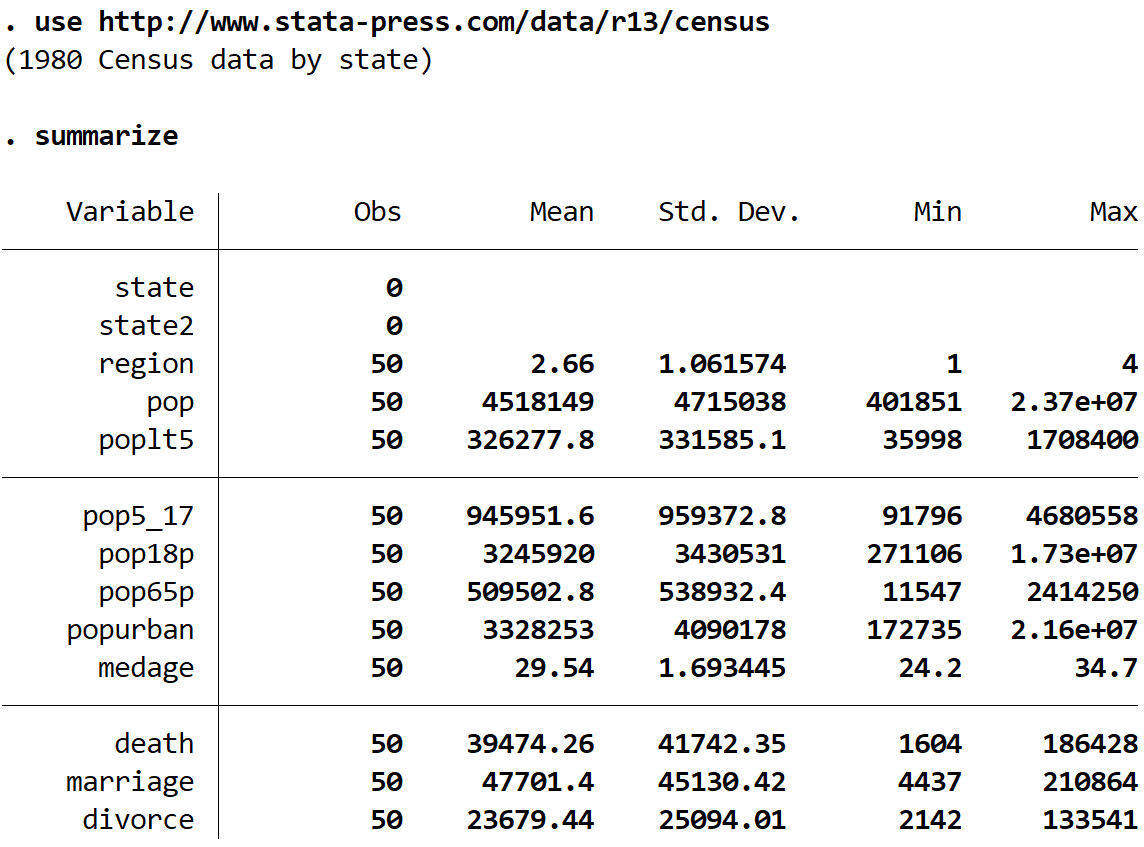
Nous pouvons voir qu’il y a 13 variables différentes dans cet ensemble de données, mais les deux seules avec lesquelles nous travaillerons sont medage (âge médian) et region .

Étape 2 : Visualisez les données.

Avant d’effectuer le test de Kruskal-Wallis, créons d’abord quelques diagrammes en boîte pour visualiser la répartition de l’âge médian pour chacune des quatre régions :

boîte graphique medage, sur (région)

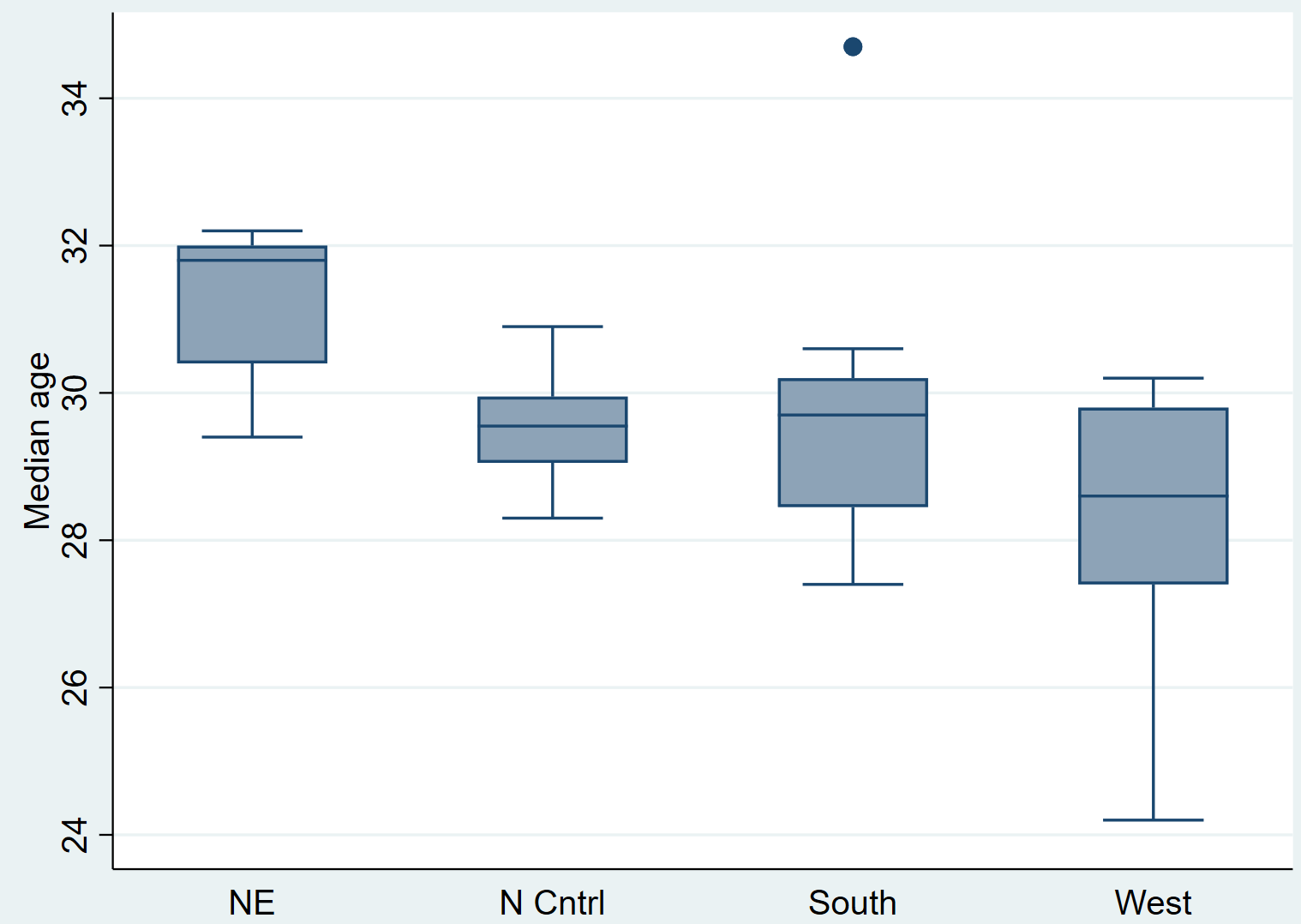
Il suffit d’examiner les diagrammes en boîte pour constater que les répartitions semblent varier d’une région à l’autre. Nous effectuerons ensuite un test de Kruskal-Wallis pour voir si ces différences sont statistiquement significatives.

Étape 3 : effectuez un test de Kruskal-Wallis.

Utilisez la syntaxe suivante pour effectuer un test de Kruskal-Wallis :

kwallis mesure_variable, par (grouping_variable)

Dans notre cas, nous utiliserons la syntaxe suivante :

kwallis medage, par (région)

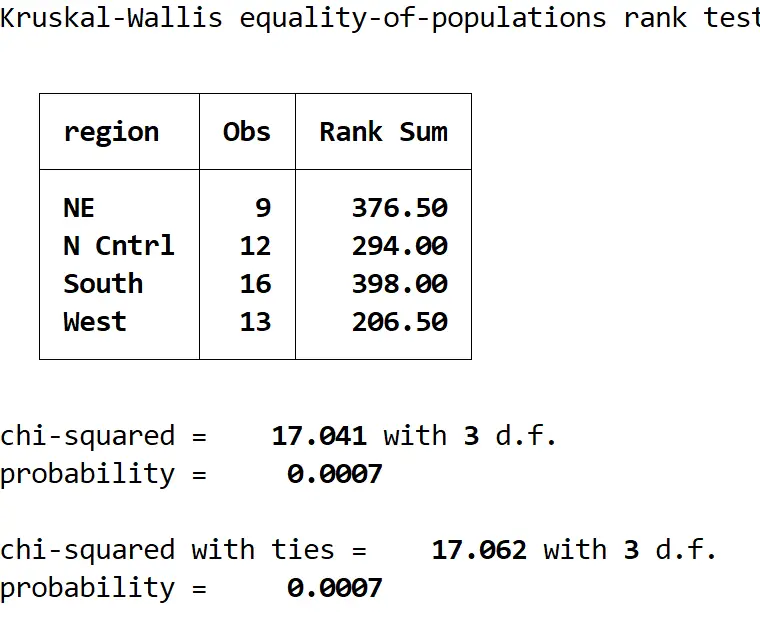
Voici comment interpréter le résultat :

Tableau récapitulatif : ce tableau montre le nombre d’observations par région et les sommes de classement pour chaque région.

Chi carré avec égalités : C’est la valeur de la statistique de test, qui s’avère être 17,062.

probabilité : Il s’agit de la valeur p qui correspond à la statistique du test, qui s’avère être 0,0007. Cette valeur étant inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle et conclure que l’âge médian n’est pas égal dans les quatre régions.

Étape 4 : Rapportez les résultats.

Enfin, nous souhaitons rapporter les résultats du test de Kruskal-Wallis. Voici un exemple de la façon de procéder :

Un test de Kruskal-Wallist a été réalisé pour déterminer si l’âge médian des individus était le même dans les quatre régions suivantes des États-Unis :

• Nord-est (n = 9)
• Centre-Nord (n = 12)
• Sud (n = 16)
• Ouest (n = 13)

Le test a révélé que l’âge médian des individus n’était pas le même (X ² = 17,062, p = 0,0007) dans les quatre régions. Autrement dit, il existait une différence statistiquement significative en termes d’âge médian entre deux ou plusieurs régions.