Régression Lasso dans R (étape par étape)

La régression Lasso est une méthode que nous pouvons utiliser pour ajuster un modèle de régression lorsque la multicolinéarité est présente dans les données.

En un mot, la régression des moindres carrés tente de trouver des estimations de coefficients qui minimisent la somme des carrés résiduels (RSS) :

RSS = Σ(y _je – ŷ _je )2

où:

• Σ : Un symbole grec qui signifie somme
• y _i : la valeur de réponse réelle pour la ^ième observation
• ŷ _i : La valeur de réponse prédite basée sur le modèle de régression linéaire multiple

À l’inverse, la régression au lasso cherche à minimiser les éléments suivants :

RSS + λΣ|β _j |

où j va de 1 à p variables prédictives et λ ≥ 0.

Ce deuxième terme de l’équation est connu sous le nom de pénalité de retrait . Dans la régression par lasso, nous sélectionnons une valeur pour λ qui produit le test MSE (erreur quadratique moyenne) le plus bas possible.

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression au lasso dans R.

Étape 1 : Charger les données

Pour cet exemple, nous utiliserons l’ensemble de données intégré de R appelé mtcars . Nous utiliserons hp comme variable de réponse et les variables suivantes comme prédicteurs :

• mpg
• poids
• merde
• qsec

Pour effectuer une régression lasso, nous utiliserons les fonctions du package glmnet . Ce package nécessite que la variable de réponse soit un vecteur et que l’ensemble des variables prédictives soit de la classe data.matrix .

Le code suivant montre comment définir nos données :

#define response variable
y <- mtcars$hp

#define matrix of predictor variables
x <- data.matrix(mtcars[, c('mpg', 'wt', 'drat', 'qsec')])

Étape 2 : Ajuster le modèle de régression Lasso

Ensuite, nous utiliserons la fonction glmnet() pour ajuster le modèle de régression lasso et spécifier alpha=1 .

Notez que définir alpha égal à 0 équivaut à utiliser la régression de crête et définir alpha à une valeur comprise entre 0 et 1 équivaut à utiliser un filet élastique.  

Pour déterminer la valeur à utiliser pour lambda, nous effectuerons une validation croisée k fois et identifierons la valeur lambda qui produit l’erreur quadratique moyenne (MSE) de test la plus faible.

Notez que la fonction cv.glmnet() effectue automatiquement une validation croisée k fois en utilisant k = 10 fois.

library(glmnet)

#perform k-fold cross-validation to find optimal lambda value
cv_model <- cv.glmnet(x, y, alpha = 1)

#find optimal lambda value that minimizes test MSE
best_lambda <- cv_model$lambda.min
best_lambda

[1] 5.616345

#produce plot of test MSE by lambda value
plot(cv_model) 

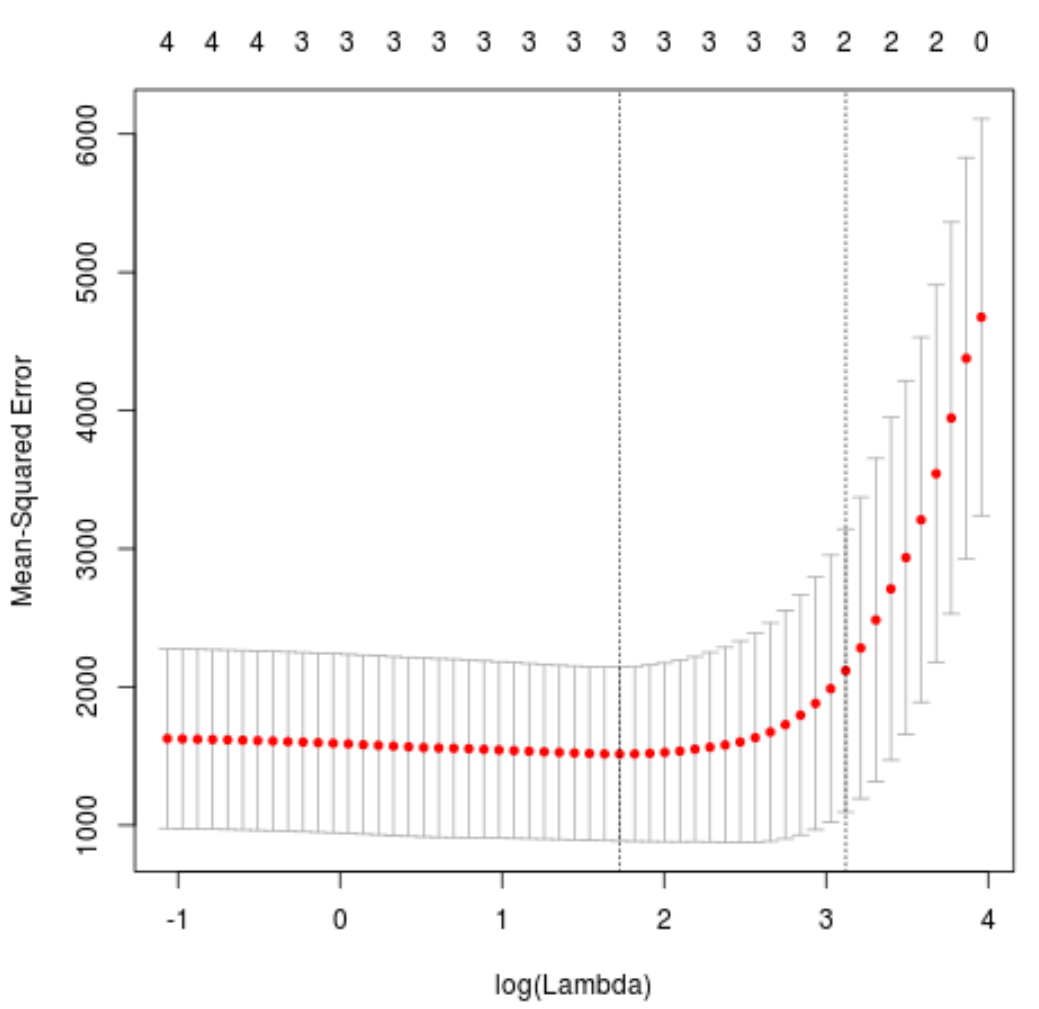
La valeur lambda qui minimise le test MSE s’avère être 5,616345 .

Étape 3 : Analyser le modèle final

Enfin, nous pouvons analyser le modèle final produit par la valeur lambda optimale.

Nous pouvons utiliser le code suivant pour obtenir les estimations de coefficients pour ce modèle :

#find coefficients of best model
best_model <- glmnet(x, y, alpha = 1, lambda = best_lambda)
coef(best_model)

5 x 1 sparse Matrix of class "dgCMatrix"
                   s0
(Intercept) 484.20742
mpg          -2.95796
wt           21.37988
drat          .      
qsec        -19.43425

Aucun coefficient n’est affiché pour le prédicteur drat car la régression du lasso a réduit le coefficient jusqu’à zéro. Cela signifie qu’il a été complètement supprimé du modèle parce qu’il n’avait pas suffisamment d’influence.

Notez qu’il s’agit d’une différence clé entre la régression par crête et la régression par lasso . La régression Ridge réduit tous les coefficients vers zéro, mais la régression lasso a le potentiel de supprimer les prédicteurs du modèle en réduisant complètement les coefficients à zéro.

Nous pouvons également utiliser le modèle de régression lasso final pour faire des prédictions sur de nouvelles observations. Par exemple, supposons que nous ayons une nouvelle voiture avec les attributs suivants :

• mpg: 24
• poids : 2,5
• prix : 3,5
• qsec : 18,5

Le code suivant montre comment utiliser le modèle de régression au lasso ajusté pour prédire la valeur hp de cette nouvelle observation :

#define new observation
new = matrix(c(24, 2.5, 3.5, 18.5), nrow=1, ncol=4) 

#use lasso regression model to predict response value
predict(best_model, s = best_lambda, newx = new)

[1,] 109.0842

Sur la base des valeurs saisies, le modèle prédit que cette voiture aura une valeur ch de 109,0842 .

Enfin, nous pouvons calculer leR-carré du modèle sur les données d’entraînement :

#use fitted best model to make predictions
y_predicted <- predict(best_model, s = best_lambda, newx = x)

#find SST and SSE
sst <- sum((y - mean(y))^2)
sse <- sum((y_predicted - y)^2)

#find R-Squared
rsq <- 1 - sse/sst
rsq

[1] 0.8047064

Le R au carré s’avère être 0,8047064 . Autrement dit, le meilleur modèle a pu expliquer 80,47 % de la variation des valeurs de réponse des données d’entraînement.

Vous pouvez trouver le code R complet utilisé dans cet exemple ici .