Comment effectuer une régression des moindres carrés pondérés dans R

L’une des hypothèses clés de la régression linéaire est que les résidus sont distribués avec une variance égale à chaque niveau de la variable prédictive. Cette hypothèse est connue sous le nom d’homoscédasticité .

Lorsque cette hypothèse n’est pas respectée, on dit que l’hétéroscédasticité est présente dans les résidus. Lorsque cela se produit, les résultats de la régression deviennent peu fiables.

Une façon de résoudre ce problème consiste à utiliser la régression des moindres carrés pondérés , qui attribue des poids aux observations de telle sorte que celles avec une faible variance d’erreur reçoivent plus de poids car elles contiennent plus d’informations par rapport aux observations avec une plus grande variance d’erreur.

Ce didacticiel fournit un exemple étape par étape de la façon d’effectuer une régression des moindres carrés de poids dans R.

Étape 1 : Créer les données

Le code suivant crée un bloc de données contenant le nombre d’heures étudiées et la note d’examen correspondante pour 16 étudiants :

df <- data.frame(hours=c(1, 1, 2, 2, 2, 3, 4, 4, 4, 5, 5, 5, 6, 6, 7, 8),
                 score=c(48, 78, 72, 70, 66, 92, 93, 75, 75, 80, 95, 97, 90, 96, 99, 99))

Étape 2 : effectuer une régression linéaire

Ensuite, nous utiliserons la fonction lm() pour ajuster un modèle de régression linéaire simple qui utilise les heures comme variable prédictive et le score comme variable de réponse :

#fit simple linear regression model
model <- lm(score ~ hours, data = df)

#view summary of model
summary(model)

Call:
lm(formula = score ~ hours, data = df)

Residuals:
    Min      1Q  Median      3Q     Max 
-17.967  -5.970  -0.719   7.531  15.032 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   60.467      5.128  11.791 1.17e-08 ***
hours          5.500      1.127   4.879 0.000244 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 9.224 on 14 degrees of freedom
Multiple R-squared:  0.6296,	Adjusted R-squared:  0.6032 
F-statistic:  23.8 on 1 and 14 DF,  p-value: 0.0002438

Étape 3 : Test d’hétéroscédasticité

Ensuite, nous allons créer un graphique des valeurs résiduelles et ajustées pour vérifier visuellement l’hétéroscédasticité :

#create residual vs. fitted plot
plot(fitted(model), resid(model), xlab='Fitted Values', ylab='Residuals')

#add a horizontal line at 0 
abline(0,0)

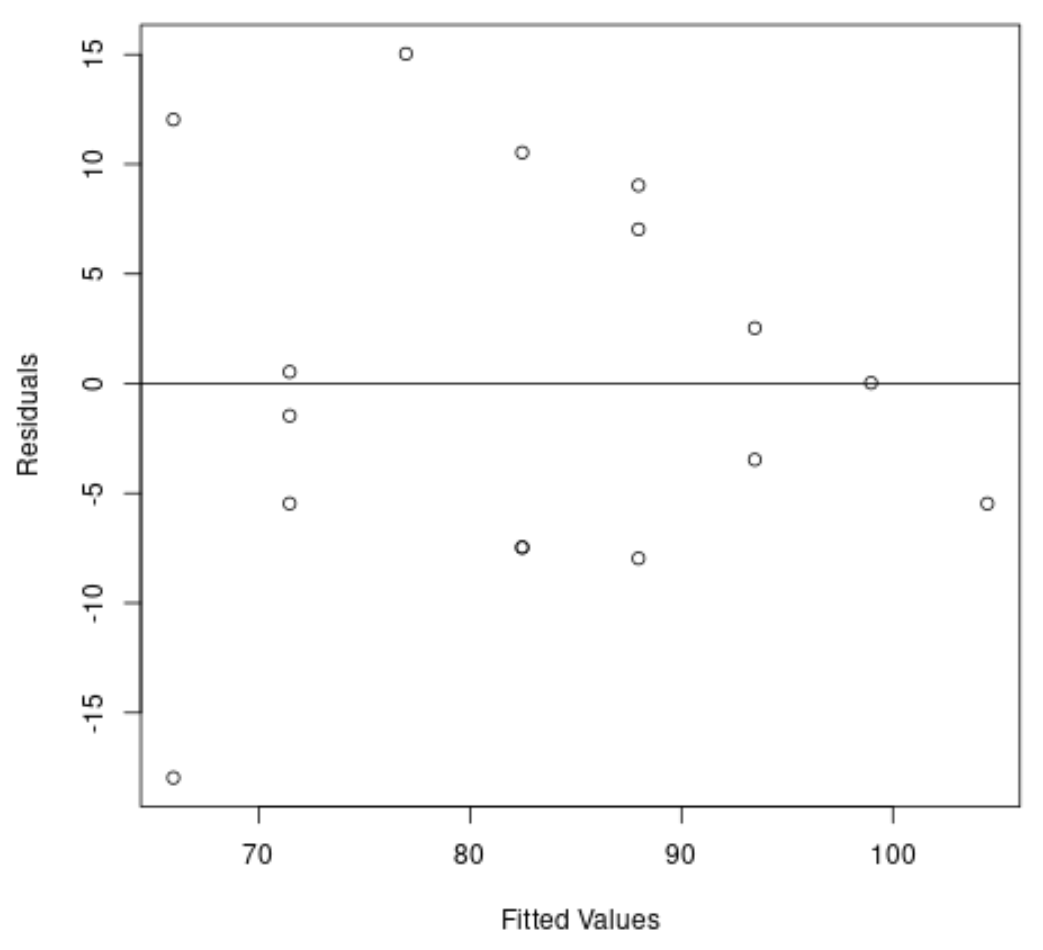
Nous pouvons voir sur le graphique que les résidus présentent une forme de « cône » : ils ne sont pas distribués avec une variance égale dans tout le graphique.

Pour tester formellement l’hétéroscédasticité, nous pouvons effectuer un test de Breusch-Pagan :

#load lmtest package
library(lmtest)

#perform Breusch-Pagan test
bptest(model)

	studentized Breusch-Pagan test

data:  model
BP = 3.9597, df = 1, p-value = 0.0466

Le test de Breusch-Pagan utilise les hypothèses nulles et alternatives suivantes :

• Hypothèse nulle (H ₀ ) : l’homoscédasticité est présente (les résidus sont distribués avec une variance égale)
• Hypothèse alternative (H _A ) : l’hétéroscédasticité est présente (les résidus ne sont pas distribués avec une variance égale)

Puisque la valeur p du test est de 0,0466 , nous rejetterons l’hypothèse nulle et conclurons que l’hétéroscédasticité constitue un problème dans ce modèle.

Étape 4 : Effectuer une régression des moindres carrés pondérés

Puisque l’hétéroscédasticité est présente, nous effectuerons des moindres carrés pondérés en définissant les poids de telle manière que les observations avec une variance plus faible reçoivent plus de poids :

#define weights to use
wt <- 1 / lm(abs(model$residuals) ~ model$fitted.values)$fitted.values^2

#perform weighted least squares regression
wls_model <- lm(score ~ hours, data = df, weights=wt)

#view summary of model
summary(wls_model)

Call:
lm(formula = score ~ hours, data = df, weights = wt)

Weighted Residuals:
    Min      1Q  Median      3Q     Max 
-2.0167 -0.9263 -0.2589  0.9873  1.6977 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  63.9689     5.1587  12.400 6.13e-09 ***
hours         4.7091     0.8709   5.407 9.24e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 1.199 on 14 degrees of freedom
Multiple R-squared:  0.6762,	Adjusted R-squared:  0.6531 
F-statistic: 29.24 on 1 and 14 DF,  p-value: 9.236e-05

À partir des résultats, nous pouvons voir que l’estimation du coefficient pour la variable prédictive heures a légèrement changé et que l’ajustement global du modèle s’est amélioré.

Le modèle des moindres carrés pondérés a une erreur type résiduelle de 1,199 , contre 9,224 dans le modèle de régression linéaire simple original.

Cela indique que les valeurs prédites produites par le modèle des moindres carrés pondérés sont beaucoup plus proches des observations réelles par rapport aux valeurs prédites produites par le modèle de régression linéaire simple.

Le modèle des moindres carrés pondérés a également un R au carré de 0,6762 , contre 0,6296 dans le modèle de régression linéaire simple d’origine.

Cela indique que le modèle des moindres carrés pondérés est capable d’expliquer une plus grande partie de la variance des résultats aux examens que le modèle de régression linéaire simple.

Ces mesures indiquent que le modèle des moindres carrés pondérés offre un meilleur ajustement aux données par rapport au modèle de régression linéaire simple.

Ressources additionnelles

Comment effectuer une régression linéaire simple dans R
Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression quantile dans R