Comment effectuer une régression OLS dans R (avec exemple)

La régression des moindres carrés ordinaires (OLS) est une méthode qui nous permet de trouver une droite qui décrit le mieux la relation entre une ou plusieurs variables prédictives et une variable de réponse .

Cette méthode nous permet de trouver l’équation suivante :

ŷ = b ₀ + b ₁ x

où:

• ŷ : La valeur de réponse estimée
• b ₀ : L’origine de la droite de régression
• b ₁ : La pente de la droite de régression

Cette équation peut nous aider à comprendre la relation entre le prédicteur et la variable de réponse, et elle peut être utilisée pour prédire la valeur d’une variable de réponse étant donné la valeur de la variable prédictive.

L’exemple étape par étape suivant montre comment effectuer une régression OLS dans R.

Étape 1 : Créer les données

Pour cet exemple, nous allons créer un ensemble de données contenant les deux variables suivantes pour 15 étudiants :

• Nombre total d’heures étudiées
• Résultat de l’examen

Nous effectuerons une régression OLS, en utilisant les heures comme variable prédictive et le score à l’examen comme variable de réponse.

Le code suivant montre comment créer ce faux ensemble de données dans R :

#create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1     1    64
2     2    66
3     4    76
4     5    73
5     5    74
6     6    81

Étape 2 : Visualisez les données

Avant d’effectuer une régression OLS, créons un nuage de points pour visualiser la relation entre les heures et la note de l’examen :

library(ggplot2)

#create scatter plot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size=2)

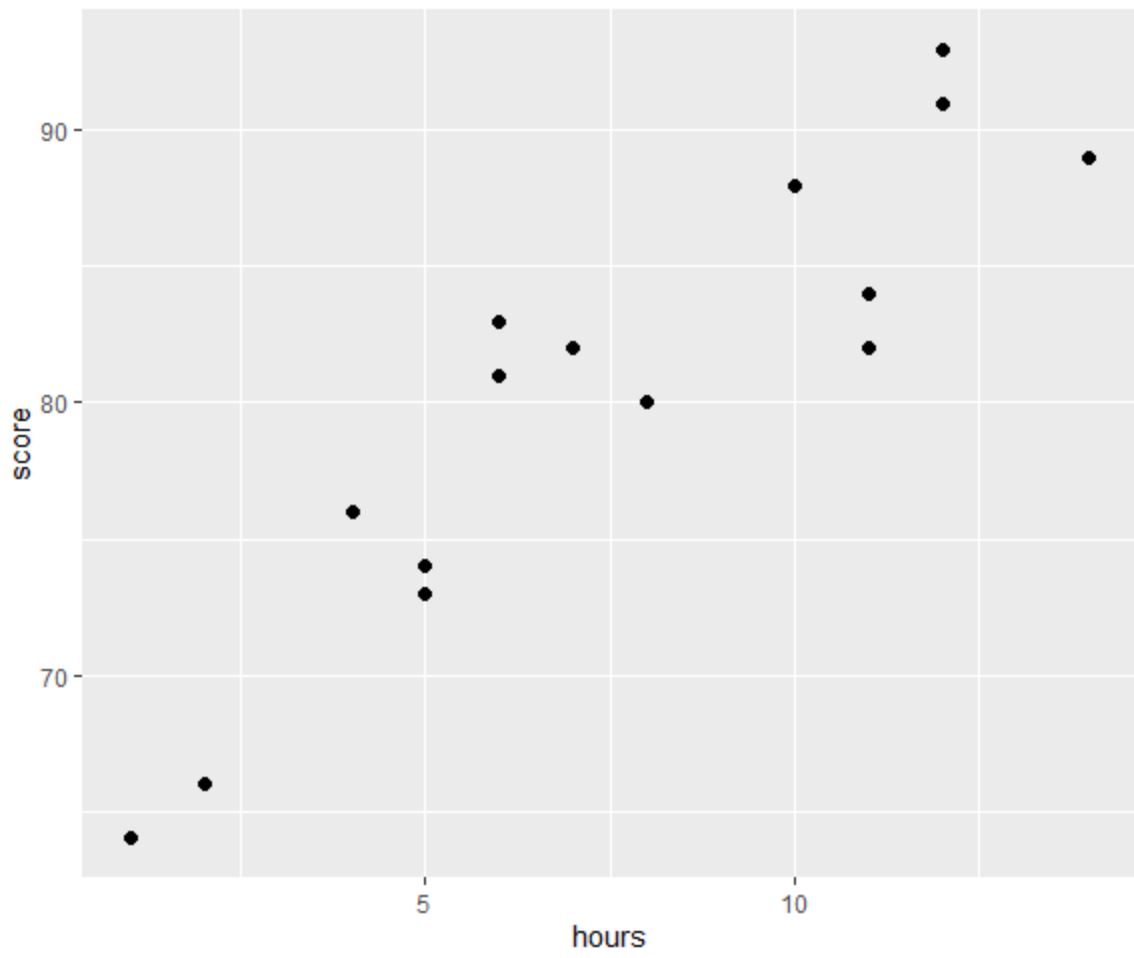
L’une des quatre hypothèses de la régression linéaire est qu’il existe une relation linéaire entre le prédicteur et la variable de réponse.

D’après le graphique, nous pouvons voir que la relation semble être linéaire. À mesure que le nombre d’heures augmente, le score a également tendance à augmenter de manière linéaire.

Ensuite, nous pouvons créer un boxplot pour visualiser la distribution des résultats des examens et vérifier les valeurs aberrantes.

Remarque : R définit une observation comme étant aberrante si elle est 1,5 fois l’intervalle interquartile supérieur au troisième quartile ou 1,5 fois l’intervalle interquartile inférieur au premier quartile.

Si une observation est aberrante, un petit cercle apparaîtra dans le boxplot :

library(ggplot2)

#create scatter plot
ggplot(df, aes(y=score)) +
  geom_boxplot()

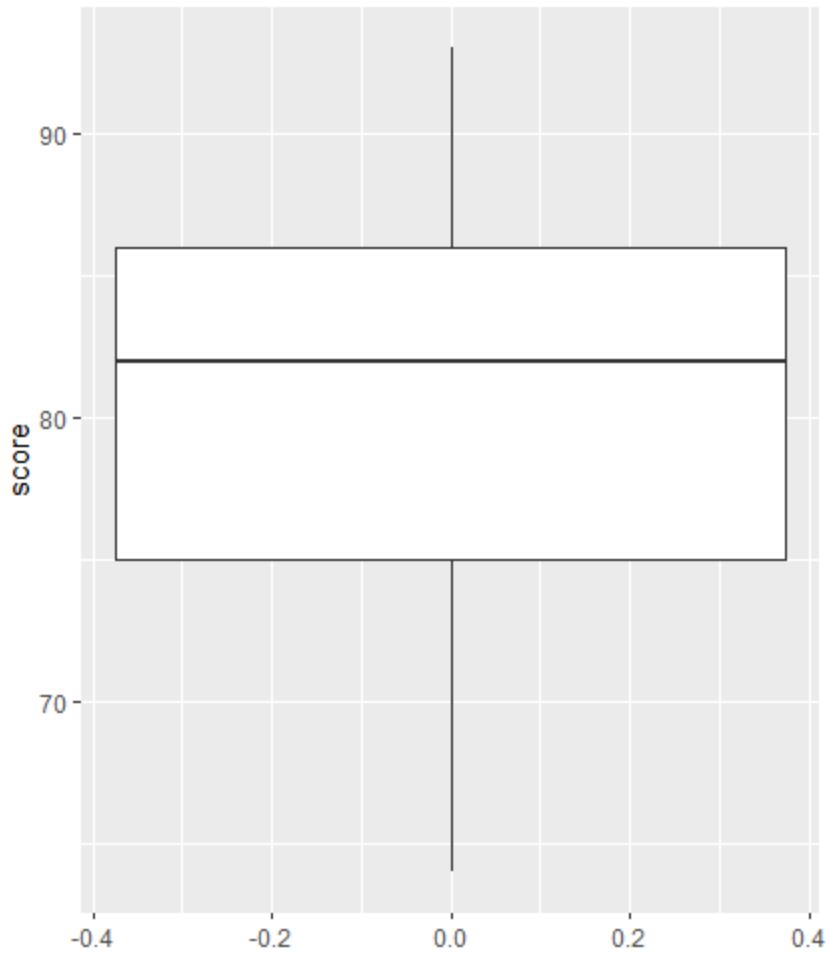
Il n’y a pas de petits cercles dans le boxplot, ce qui signifie qu’il n’y a pas de valeurs aberrantes dans notre ensemble de données.

Étape 3 : effectuer une régression OLS

Ensuite, nous pouvons utiliser la fonction lm() dans R pour effectuer une régression OLS, en utilisant les heures comme variable prédictive et le score comme variable de réponse :

#fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min     1Q Median     3Q    Max 
-5.140 -3.219 -1.193  2.816  5.772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   65.334      2.106  31.023 1.41e-13 ***
hours          1.982      0.248   7.995 2.25e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared:  0.831,	Adjusted R-squared:  0.818 
F-statistic: 63.91 on 1 and 13 DF,  p-value: 2.253e-06

À partir du résumé du modèle, nous pouvons voir que l’équation de régression ajustée est :

Score = 65,334 + 1,982*(heures)

Cela signifie que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de la note à l’examen de 1,982 points.

La valeur d’origine de 65,334 nous indique la note moyenne attendue à l’examen pour un étudiant qui étudie zéro heure.

Nous pouvons également utiliser cette équation pour trouver la note attendue à l’examen en fonction du nombre d’heures qu’un étudiant étudie.

Par exemple, un étudiant qui étudie pendant 10 heures devrait obtenir une note à l’examen de 85,15 :

Note = 65,334 + 1,982*(10) = 85,15

Voici comment interpréter le reste du résumé du modèle :

• Pr(>|t|) : Il s’agit de la valeur p associée aux coefficients du modèle. Étant donné que la valeur p pour les heures (2,25e-06) est nettement inférieure à 0,05, nous pouvons dire qu’il existe une association statistiquement significative entre les heures et le score .
• R-carré multiple : ce nombre nous indique que le pourcentage de variation des résultats de l’examen peut s’expliquer par le nombre d’heures étudiées. En général, plus la valeur R au carré d’un modèle de régression est grande, plus les variables prédictives sont capables de prédire la valeur de la variable de réponse. Dans ce cas, 83,1 % de la variation des scores peut être expliquée par les heures étudiées.
• Erreur type résiduelle : il s’agit de la distance moyenne entre les valeurs observées et la ligne de régression. Plus cette valeur est faible, plus une droite de régression est capable de correspondre aux données observées. Dans ce cas, le score moyen observé à l’examen s’écarte de 3,641 points du score prédit par la droite de régression.
• Statistique F et valeur p : La statistique F ( 63,91 ) et la valeur p correspondante ( 2,253e-06 ) nous indiquent la signification globale du modèle de régression, c’est-à-dire si les variables prédictives du modèle sont utiles pour expliquer la variation. dans la variable de réponse. Étant donné que la valeur p dans cet exemple est inférieure à 0,05, notre modèle est statistiquement significatif et les heures sont considérées comme utiles pour expliquer la variation du score .

Étape 4 : Créer des tracés résiduels

Enfin, nous devons créer des tracés résiduels pour vérifier les hypothèses d’ homoscédasticité et de normalité .

L’hypothèse d’ homoscédasticité est que les résidus d’un modèle de régression ont une variance à peu près égale à chaque niveau d’une variable prédictive.

Pour vérifier que cette hypothèse est remplie, nous pouvons créer un graphique des résidus par rapport aux ajustements .

L’axe des x affiche les valeurs ajustées et l’axe des y affiche les résidus. Tant que les résidus semblent être répartis de manière aléatoire et uniforme dans tout le graphique autour de la valeur zéro, nous pouvons supposer que l’homoscédasticité n’est pas violée :

#define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

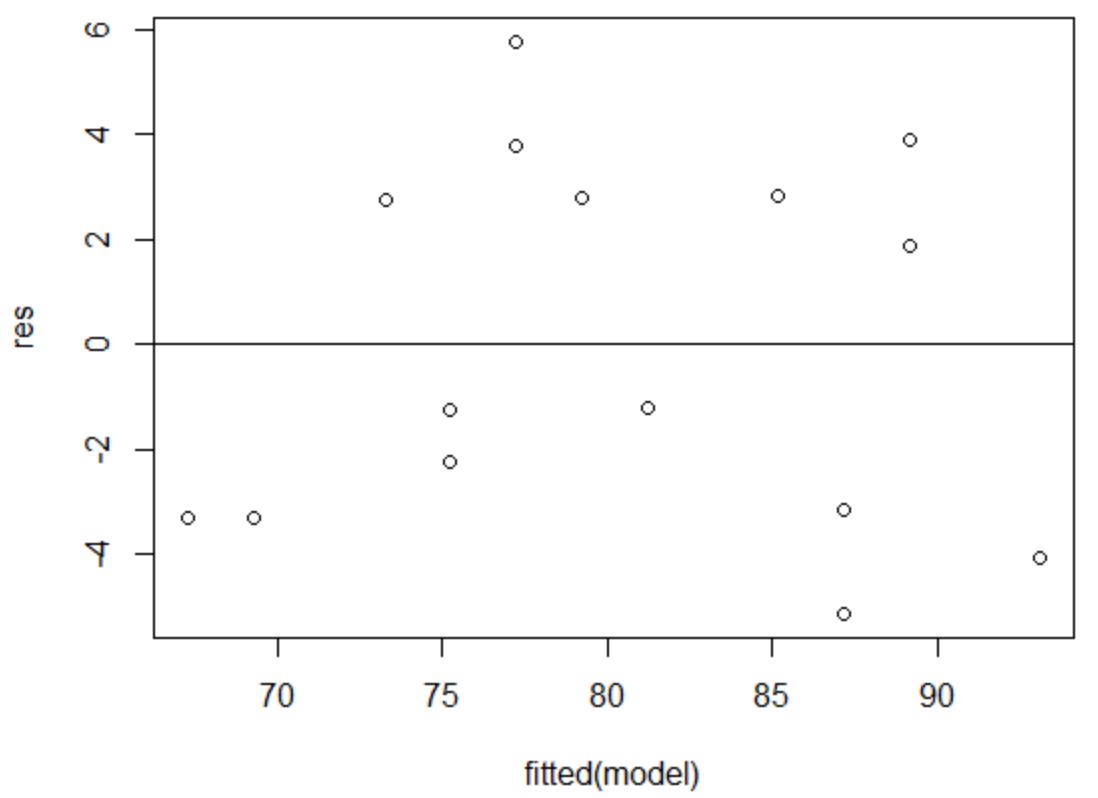
Les résidus semblent être dispersés de manière aléatoire autour de zéro et ne présentent aucun modèle notable, cette hypothèse est donc remplie.

L’hypothèse de normalité stipule que les résidus d’un modèle de régression sont à peu près normalement distribués.

Pour vérifier si cette hypothèse est remplie, nous pouvons créer un tracé QQ . Si les points du tracé se situent le long d’une ligne à peu près droite formant un angle de 45 degrés, alors les données sont normalement distribuées :

#create Q-Q plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

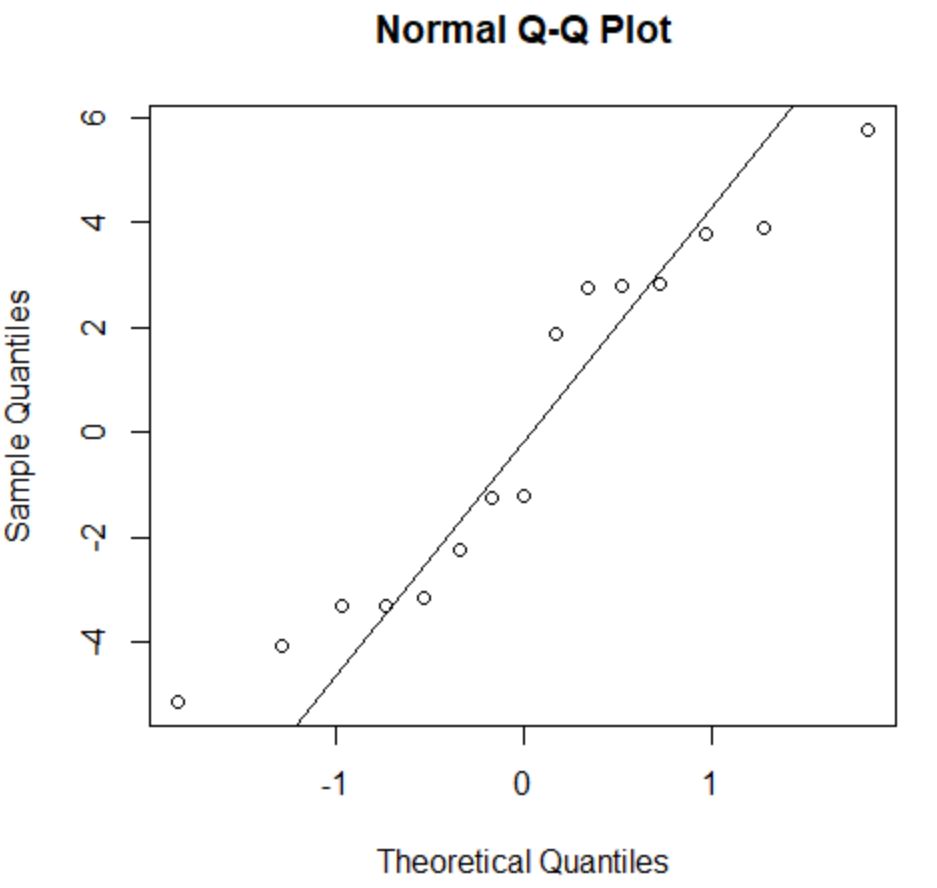
Les résidus s’écartent un peu de la ligne des 45 degrés, mais pas suffisamment pour susciter de sérieuses inquiétudes. Nous pouvons supposer que l’hypothèse de normalité est remplie.

Puisque les résidus sont normalement distribués et homoscédastiques, nous avons vérifié que les hypothèses du modèle de régression OLS sont remplies.

Ainsi, la sortie de notre modèle est fiable.

Remarque : Si une ou plusieurs des hypothèses n’étaient pas remplies, nous pourrions tenter de transformer nos données.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans R :

Comment effectuer une régression linéaire multiple dans R
Comment effectuer une régression exponentielle dans R
Comment effectuer une régression des moindres carrés pondérés dans R