Jak wykonać regresję liniową na kalkulatorze ti-84

Regresja liniowa to metoda, której możemy użyć do zrozumienia związku między zmienną objaśniającą x i zmienną odpowiedzi y.

W tym samouczku wyjaśniono, jak przeprowadzić regresję liniową na kalkulatorze TI-84.

Przykład: regresja liniowa na kalkulatorze TI-84

Załóżmy, że chcemy zrozumieć związek pomiędzy liczbą godzin, jakie student przygotowuje się do egzaminu, a oceną, jaką otrzymuje z egzaminu.

Aby zbadać tę zależność, możemy wykonać następujące kroki na kalkulatorze TI-84, aby przeprowadzić prostą regresję liniową, wykorzystując przepracowane godziny jako zmienną objaśniającą i ocenę z egzaminu jako zmienną odpowiedzi.

Krok 1: Wprowadź dane.

Najpierw wprowadzimy wartości danych dla zmiennej objaśniającej i zmiennej odpowiedzi. Naciśnij Stat , następnie naciśnij EDYTUJ . Wpisz następujące wartości zmiennej objaśniającej (godziny nauki) w kolumnie L1 i wartości zmiennej odpowiedzi (wynik z egzaminu) w kolumnie L2:

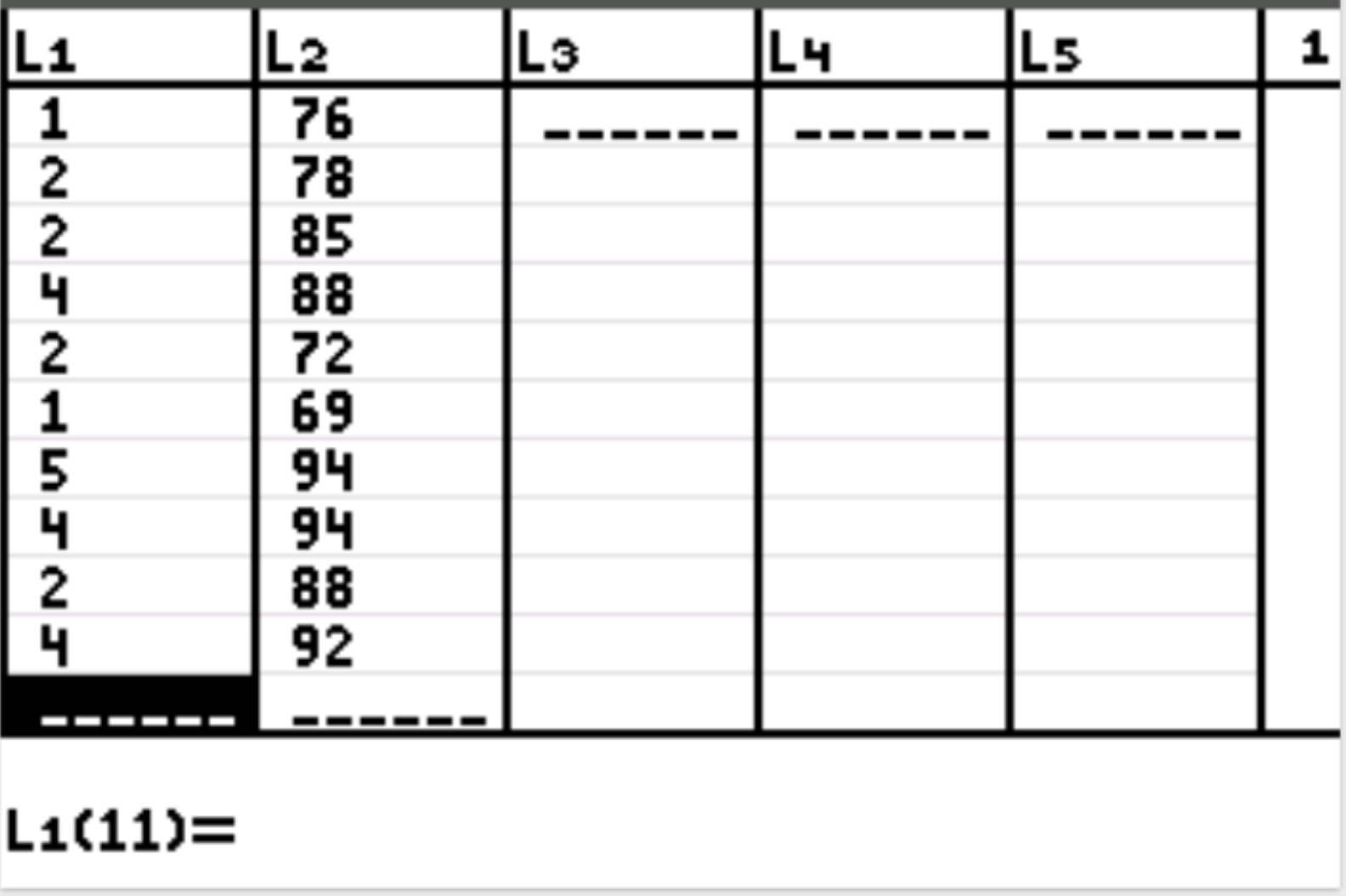
Krok 2: Wykonaj regresję liniową.

Następnie przeprowadzimy regresję liniową. Naciśnij Stat, a następnie przewiń do CALC . Następnie przewiń do 8: Linreg(a+bx) i naciśnij Enter .

W przypadku Xlist i Ylist upewnij się, że wybrano L1 i L2, ponieważ są to kolumny, których użyliśmy do wprowadzenia naszych danych. Pozostaw listę FreqList pustą. Przewiń w dół do Oblicz i naciśnij Enter . Następujące dane wyjściowe pojawią się automatycznie:

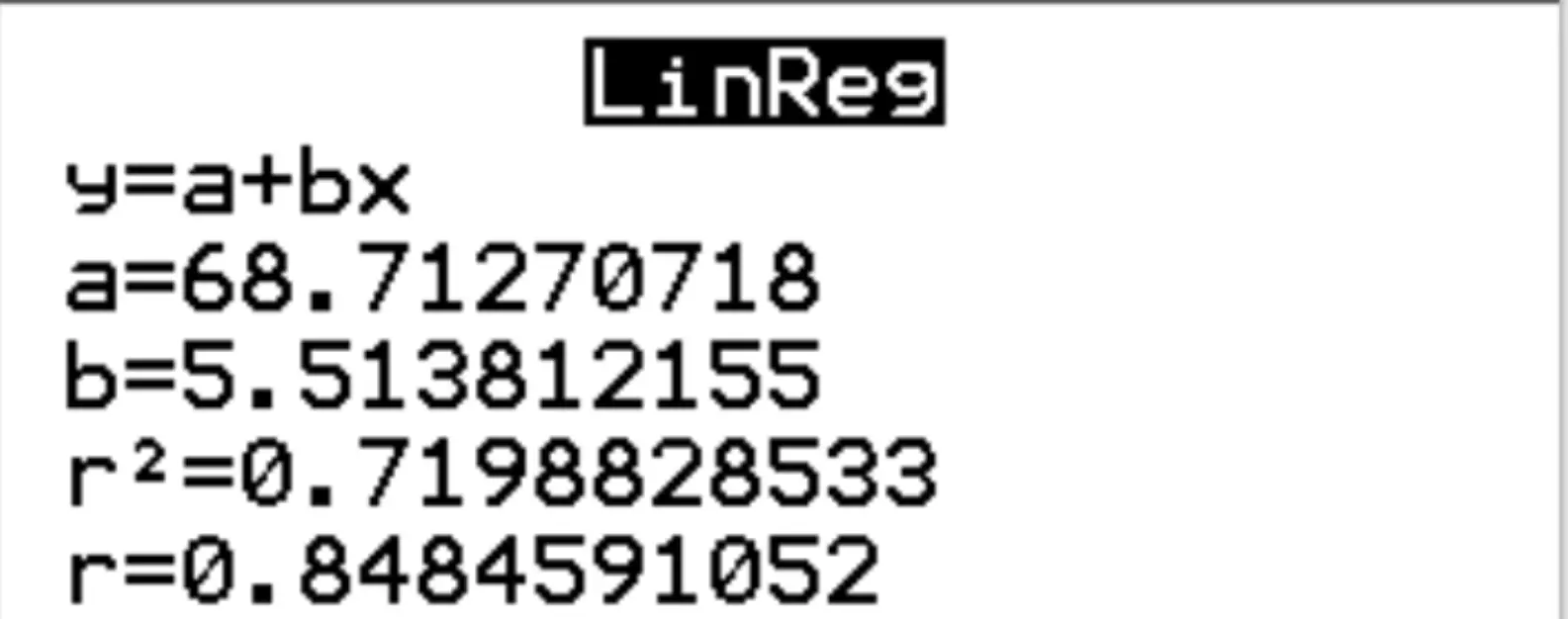
Krok 3: Interpretacja wyników.

Z wyników widzimy, że oszacowane równanie regresji ma postać:

wynik egzaminu = 68,7127 + 5,5138*(godziny)

Współczynnik godzin interpretujemy w ten sposób, że za każdą dodatkową przestudiowaną godzinę wynik egzaminu powinien wzrosnąć średnio o 5,5138 . Interpretujemy współczynnik przecięcia w ten sposób, że oczekiwany wynik egzaminu dla studenta studiującego zero godzin wynosi 68,7127 .

Możemy użyć tego szacunkowego równania regresji do obliczenia oczekiwanego wyniku egzaminu dla studenta na podstawie liczby godzin nauki.

Na przykład student studiujący trzy godziny powinien uzyskać wynik egzaminu 85,25 :

wynik egzaminu = 68,7127 + 5,5138*(3) = 85,25

Widzimy również, że r kwadrat dla modelu regresji wynosi r ² = 0,7199 .

Wartość ta nazywana jest współczynnikiem determinacji. Jest to proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej objaśniającej. W tym przykładzie 71,99% różnic w wynikach egzaminów można wyjaśnić liczbą godzin nauki.

Dodatkowe zasoby

Jak utworzyć wykres pozostałości na kalkulatorze TI-84
Jak wykonać regresję kwadratową na kalkulatorze TI-84
Jak przeprowadzić regresję wykładniczą na kalkulatorze TI-84
Jak wykonać regresję logarytmiczną na kalkulatorze TI-84