Kiedy należy stosować regresję wielomianową?

Regresja wielomianowa to technika, której możemy użyć do dopasowania modelu regresji, gdy związek między zmiennymi predykcyjnymi a zmienną odpowiedzi jest nieliniowy.

Model regresji wielomianowej ma następującą postać:

Y = β ₀ ⁺ β ₁ X + β ₂ X ² + … + β _godz

W praktyce istnieją trzy proste sposoby ustalenia, czy należy zastosować regresję wielomianową, czy prostszy model, taki jak regresja liniowa .

1. Utwórz wykres rozrzutu zmiennej predykcyjnej i zmiennej odpowiedzi

Najłatwiejszym sposobem ustalenia, czy należy zastosować regresję wielomianową, jest utworzenie prostego wykresu rozrzutu zmiennej predykcyjnej i zmiennej odpowiedzi.

Załóżmy na przykład, że chcemy użyć zmiennej predykcyjnej „godziny nauki”, aby przewidzieć ocenę, jaką uczeń otrzyma z egzaminu końcowego.

Przed dopasowaniem modelu regresji możemy najpierw stworzyć wykres rozrzutu godzin przestudiowanych w porównaniu z wynikami egzaminu. Załóżmy, że nasz wykres rozrzutu wygląda następująco:

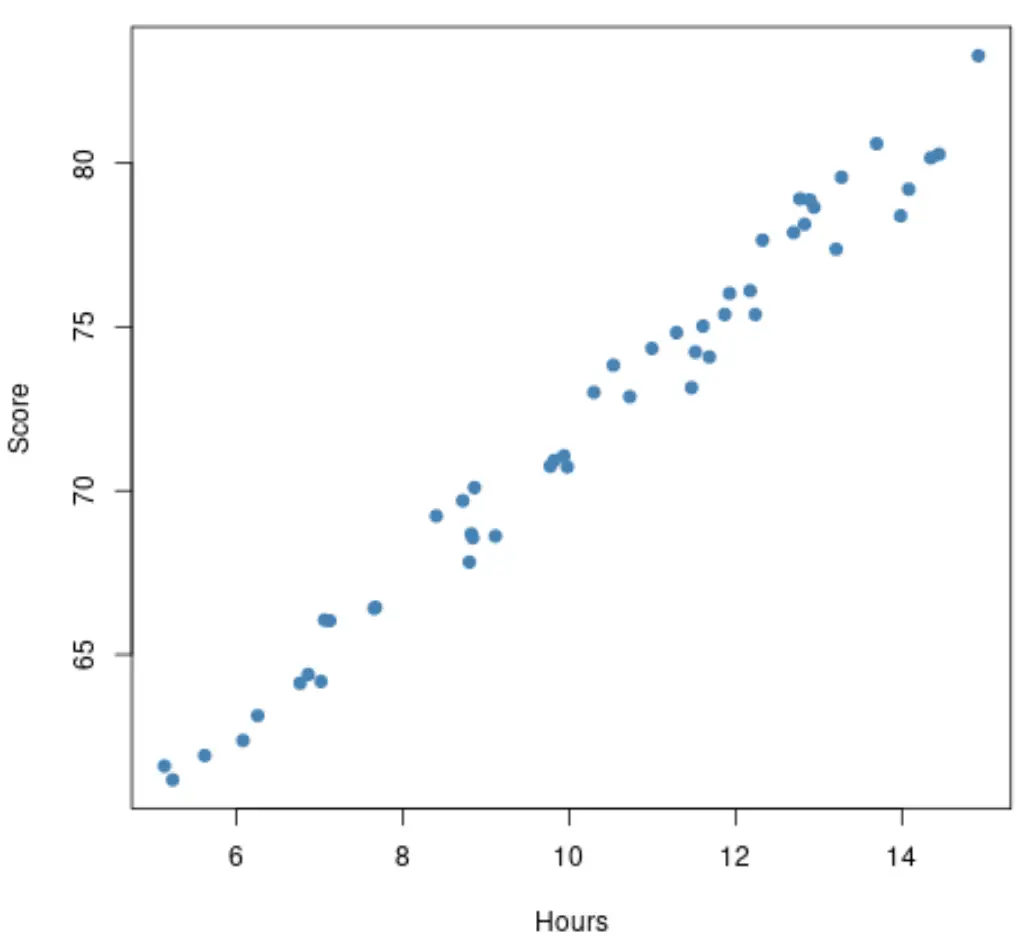
Zależność między przepracowanymi godzinami a wynikami egzaminów wydaje się liniowa , zatem sensowne byłoby dopasowanie do tego zbioru danych prostego modelu regresji liniowej.

Załóżmy jednak, że wykres rozrzutu w rzeczywistości wygląda następująco:

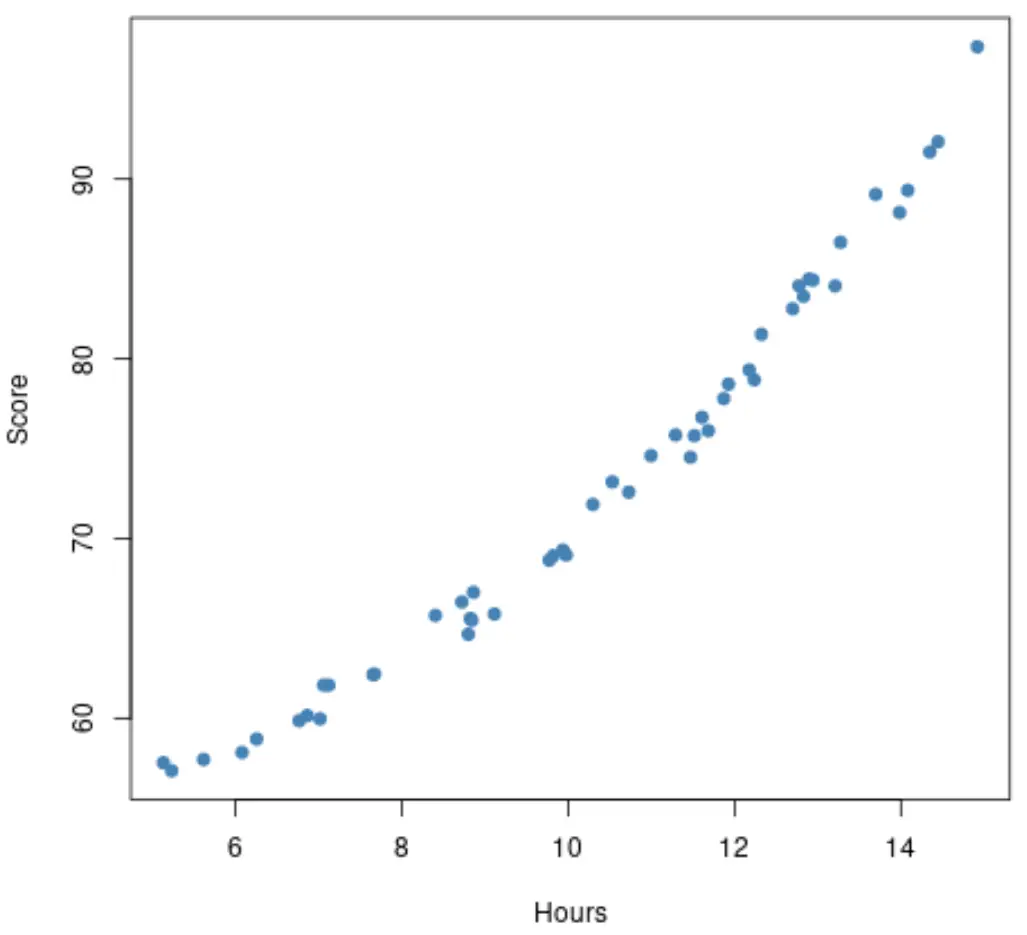
Zależność ta wydaje się nieco bardziej nieliniowa , co mówi nam, że rozsądniejszym rozwiązaniem może być dopasowanie modelu regresji wielomianowej.

2. Utwórz wykres wartości dopasowanych i resztowych

Innym sposobem ustalenia, czy należy zastosować regresję wielomianową, jest dopasowanie modelu regresji liniowej do zbioru danych, a następnie utworzenie wykresu dopasowanych wartości względem reszt modelu.

Jeżeli w resztach występuje wyraźny nieliniowy trend, oznacza to, że regresja wielomianowa może zapewnić lepsze dopasowanie danych.

Załóżmy na przykład, że dopasowujemy model regresji liniowej, wykorzystując przestudiowane godziny jako zmienną predykcyjną i wynik egzaminu jako zmienną odpowiedzi, a następnie tworzymy następujący wykres dopasowanych wartości w funkcji reszt:

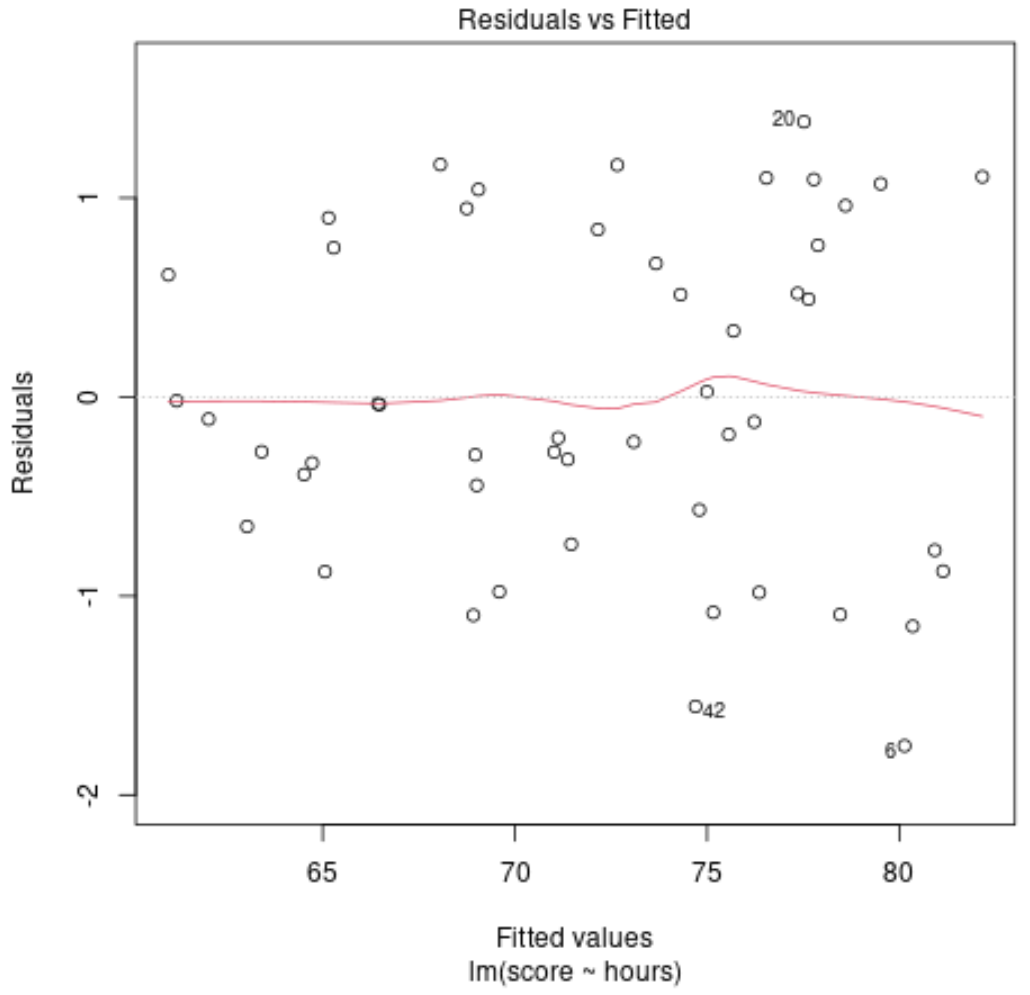
Reszty są losowo rozproszone wokół zera, bez wyraźnego wzoru, co wskazuje, że model liniowy zapewnia odpowiednie dopasowanie do danych.

Załóżmy jednak, że nasz wykres dopasowanych wartości względem reszt w rzeczywistości wygląda następująco:

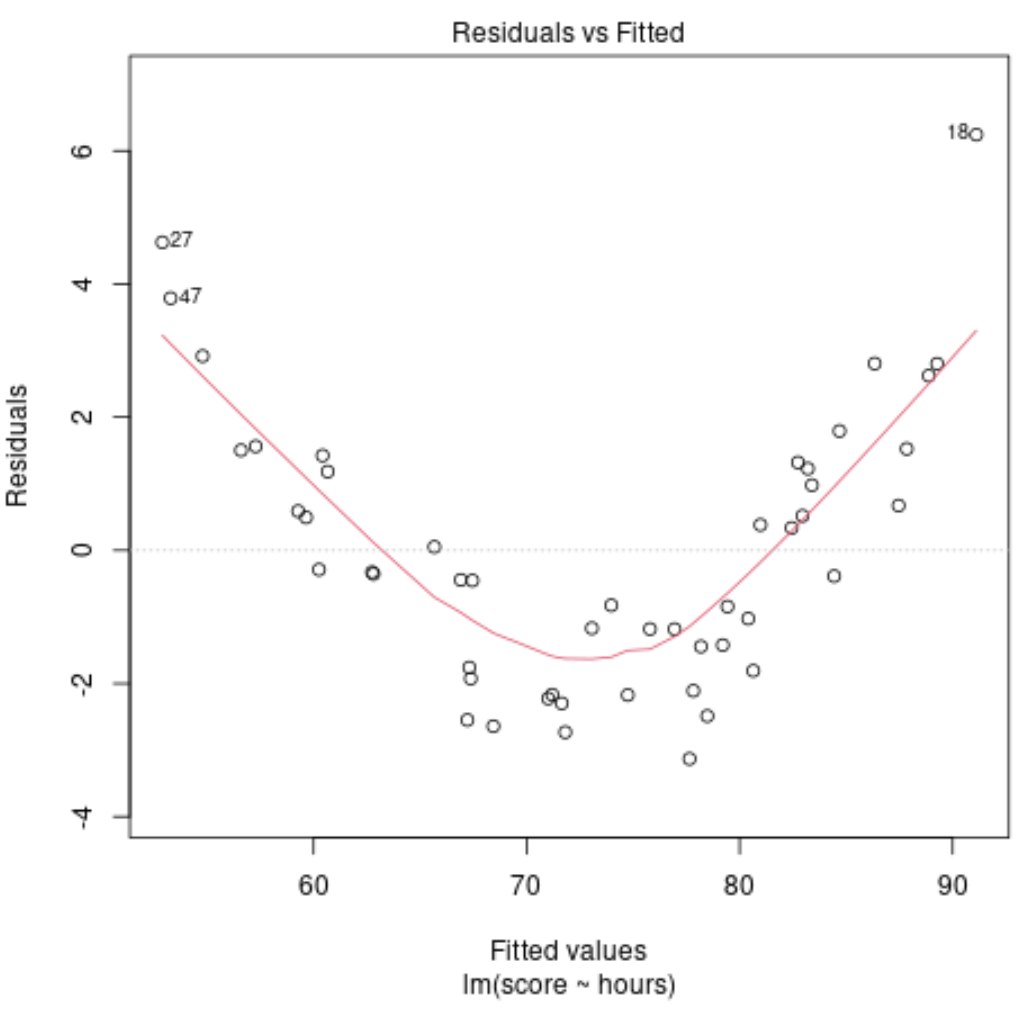
Z wykresu widać, że reszty mają wyraźny nieliniowy wzór – reszty mają kształt litery „U”.

To mówi nam, że model liniowy nie jest odpowiedni dla tych konkretnych danych i że mądrzej byłoby zamiast tego dopasować model regresji wielomianowej.

3. Oblicz skorygowaną wartość R-kwadrat modelu

Innym sposobem ustalenia, czy należy zastosować regresję wielomianową, jest dopasowanie zarówno modelu regresji liniowej, jak i modelu regresji wielomianowej i obliczenie dopasowanych wartości R-kwadrat dla obu modeli.

Skorygowany R-kwadrat reprezentuje część wariancji zmiennej odpowiedzi, którą można wyjaśnić zmiennymi predykcyjnymi w modelu, skorygowaną o liczbę zmiennych predykcyjnych w modelu.

Model z najwyższym skorygowanym kwadratem R reprezentuje model, który najlepiej potrafi wykorzystać zmienne predykcyjne do wyjaśnienia zmienności zmiennej odpowiedzi.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak przeprowadzić regresję wielomianową przy użyciu różnych programów statystycznych:

Wprowadzenie do regresji wielomianowej
Jak wykonać regresję wielomianową w R
Jak wykonać regresję wielomianową w Pythonie
Jak wykonać regresję wielomianową w programie Excel