Co to jest regresja krzywoliniowa? (definicja i przykłady)
Regresja krzywoliniowa to nazwa nadana każdemu modelowi regresji, który próbuje dopasować krzywą , a nie linię prostą.
Typowe przykłady modeli regresji krzywoliniowej obejmują:
Regresja kwadratowa: stosowana, gdy istnieje zależność kwadratowa między zmienną predykcyjną azmienną odpowiedzi . Na wykresie ten typ relacji wygląda jak „U” lub odwrócone „U” na wykresie punktowym:
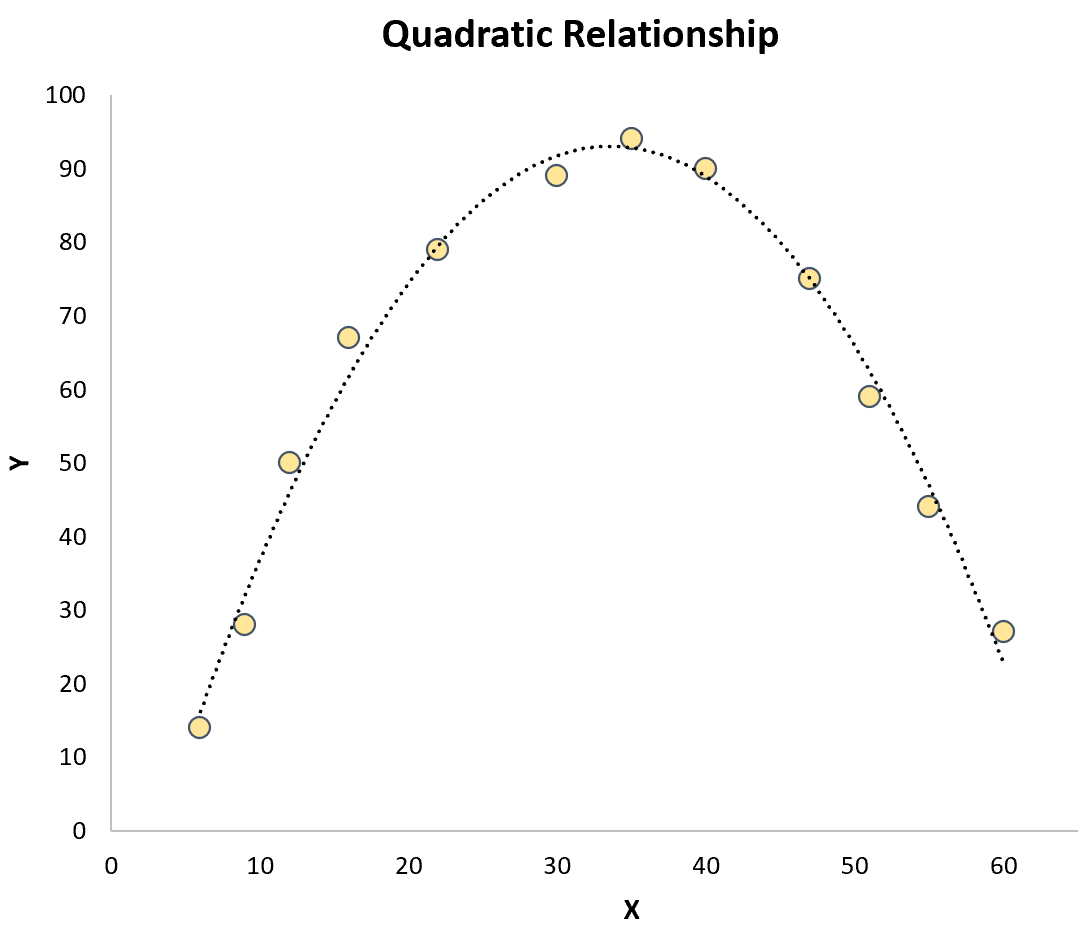
Regresja sześcienna: stosowana, gdy istnieje relacja sześcienna pomiędzy zmienną predykcyjną a zmienną odpowiedzi. Na wykresie ten typ relacji przedstawia dwie różne krzywe na wykresie rozrzutu:
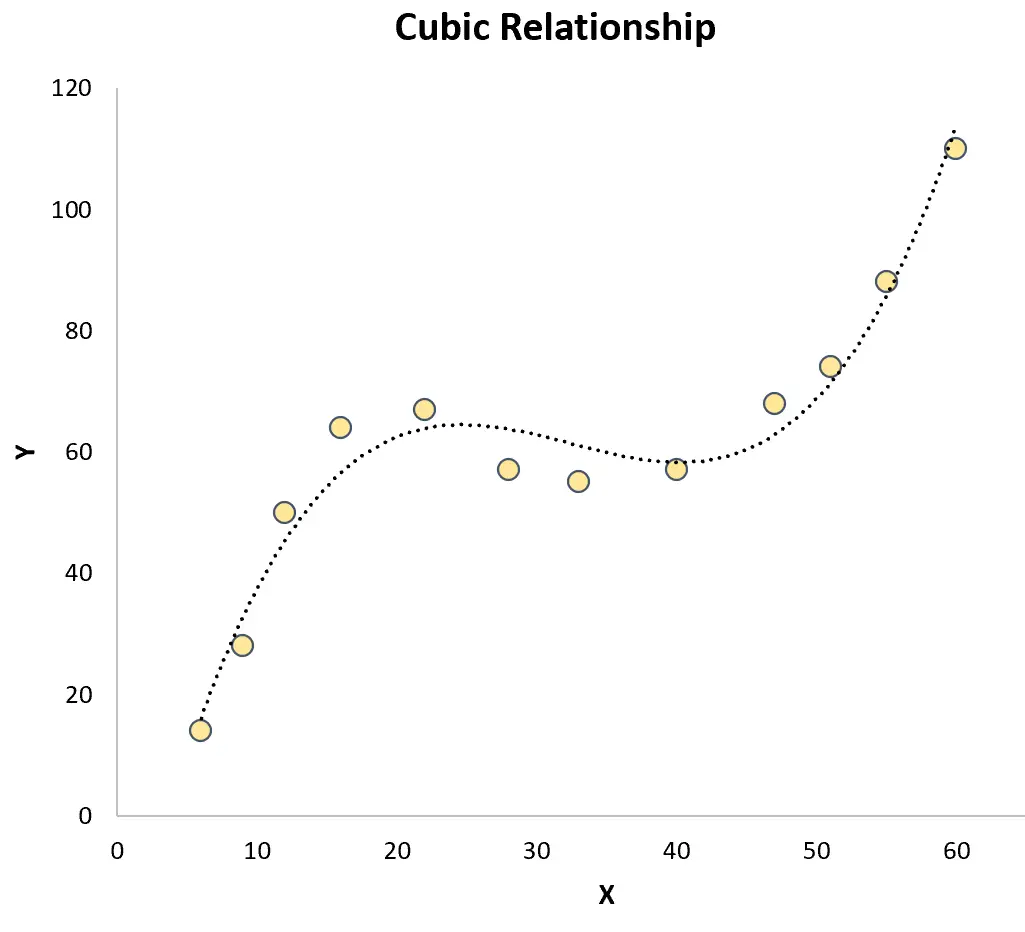
Obydwa kontrastują z prostą regresją liniową , w której związek między zmienną predykcyjną a zmienną odpowiedzi jest liniowy:
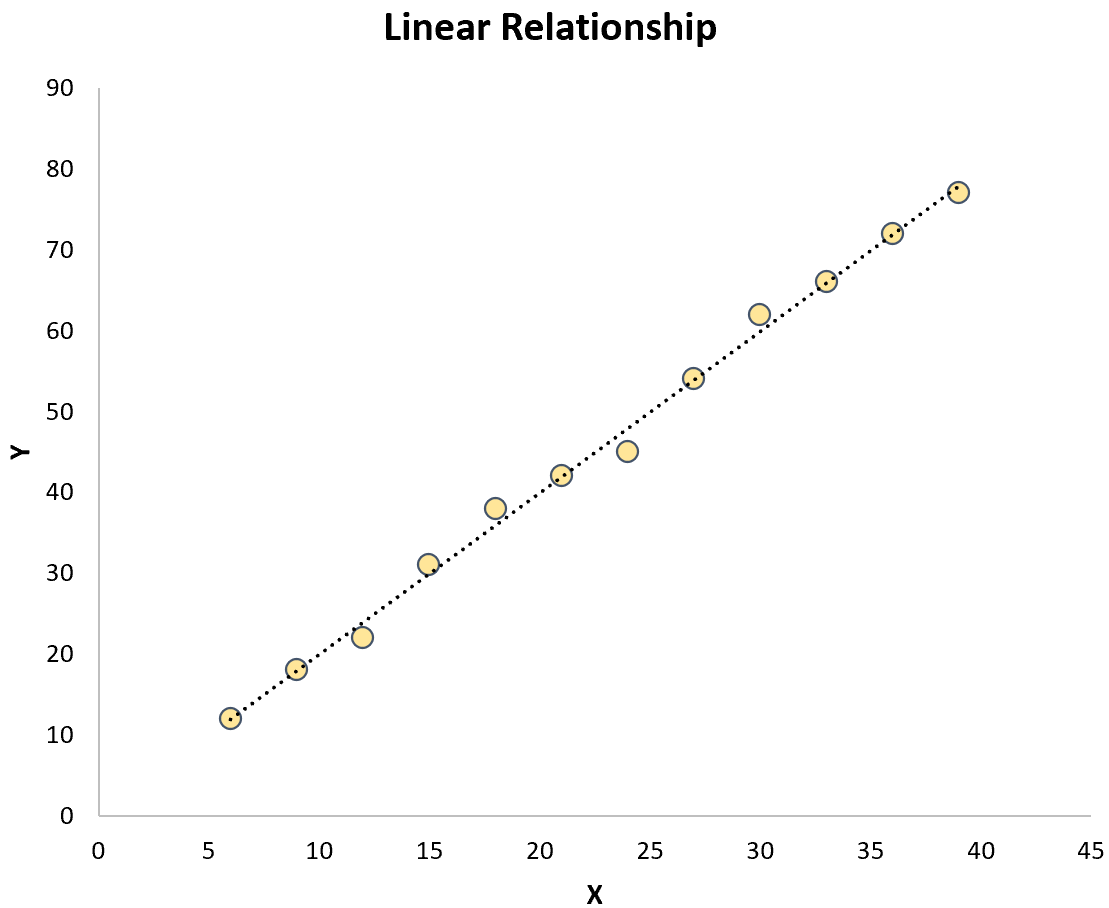
Wzór na modele regresji krzywoliniowej
Prosty model regresji liniowej próbuje dopasować zbiór danych za pomocą następującego wzoru:
ŷ = β 0 + β 1 x
Złoto:
- ŷ: Zmienna odpowiedzi
- β 0 , β 1 : Współczynniki regresji
- x: zmienna predykcyjna
Natomiast model regresji kwadratowej wykorzystuje następujący wzór:
ŷ = β 0 + β 1 x + β 2 x 2
Model regresji sześciennej wykorzystuje następujący wzór:
ŷ = β 0 + β 1 x + β 2 x 2 + β 3 x 3
Bardziej ogólną nazwą nadawaną modelom regresji zawierającym wykładniki jest regresja wielomianowa , która przyjmuje następujący wzór:
ŷ = β 0 + β 1 x + β 2 x 2 + … + β k x k
Wartość k wskazuje stopień wielomianu. Chociaż stopień może być dowolną liczbą dodatnią, w praktyce rzadko dopasowujemy modele regresji wielomianowej ze stopniem większym niż 3 lub 4.
Używając wykładników we wzorze modelu regresji, modele regresji wielomianowej mogą dopasowywać krzywe do zbiorów danych zamiast linii prostych.
Kiedy stosować regresję krzywoliniową
Najłatwiejszym sposobem sprawdzenia, czy należy zastosować regresję krzywoliniową, jest utworzenie wykresu rozrzutu zmiennej predykcyjnej i zmiennej odpowiedzi.
Jeśli wykres rozrzutu pokazuje liniową zależność między dwiema zmiennymi, prawdopodobnie właściwa będzie prosta regresja liniowa.
Jeśli jednak wykres rozrzutu przedstawia wzór kwadratowy, sześcienny lub inny krzywoliniowy pomiędzy predyktorem a zmienną odpowiedzi, wówczas prawdopodobnie bardziej odpowiednie będzie zastosowanie regresji krzywoliniowej.
Można także dopasować prosty model regresji liniowej i model regresji krzywoliniowej oraz porównać dopasowane wartości R-kwadrat każdego modelu, aby określić, który model zapewnia najlepsze dopasowanie do danych.
Skorygowany współczynnik R-kwadrat jest przydatny, ponieważ informuje, jaką część wariancji zmiennej odpowiedzi można wyjaśnić za pomocą zmiennych predykcyjnych skorygowanych o liczbę zmiennych predykcyjnych w modelu.
Ogólnie rzecz biorąc, model o najwyższej skorygowanej wartości R-kwadrat zapewnia lepsze dopasowanie do zbioru danych.
Dodatkowe zasoby
Poniższe samouczki wyjaśniają, jak przeprowadzić regresję wielomianową w różnych programach statystycznych:
Wprowadzenie do regresji wielomianowej
Jak wykonać regresję wielomianową w programie Excel
Jak wykonać regresję wielomianową w Pythonie
Jak wykonać regresję wielomianową w R
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej