Wprowadzenie do regresji wielomianowej
Kiedy mamy zbiór danych zawierający zmienną predykcyjną i zmienną odpowiedzi , często używamy prostej regresji liniowej, aby określić ilościowo związek między tymi dwiema zmiennymi.
Jednak prosta regresja liniowa (SLR) zakłada, że związek między predyktorem a zmienną odpowiedzi jest liniowy. Zapisany w notacji matematycznej SLR zakłada, że zależność ma postać:
Y = β 0 + β 1 X + ε
Jednak w praktyce związek między tymi dwiema zmiennymi może w rzeczywistości być nieliniowy, a próba zastosowania regresji liniowej może skutkować słabo dopasowanym modelem.
Jednym ze sposobów wyjaśnienia nieliniowej zależności między predyktorem a zmienną odpowiedzi jest użycie regresji wielomianowej , która przyjmuje postać:
Y = β 0 + β 1 X + β 2 X 2 + … + β godz
W tym równaniu h nazywa się stopniem wielomianu.
Gdy zwiększamy wartość h , model jest w stanie lepiej uwzględnić zależności nieliniowe, ale w praktyce rzadko wybieramy wartość h większą niż 3 lub 4. Powyżej tego punktu model staje się zbyt elastyczny i nadmiernie dopasowuje się do danych .
Uwagi techniczne
- Chociaż regresja wielomianowa może pasować do danych nieliniowych, nadal jest uważana za formę regresji liniowej , ponieważ jest liniowa pod względem współczynników β1 , β2 ,…, βh .
- Regresję wielomianową można również zastosować w przypadku wielu zmiennych predykcyjnych, ale powoduje to utworzenie w modelu składników interakcji, co może uczynić model niezwykle złożonym, jeśli używanych jest wiele zmiennych predykcyjnych.
Kiedy stosować regresję wielomianową
Regresji wielomianowej używamy, gdy związek między predyktorem a zmienną odpowiedzi jest nieliniowy.
Istnieją trzy typowe sposoby wykrywania zależności nieliniowej:
1. Utwórz wykres rozrzutu.
Najprostszym sposobem wykrycia zależności nieliniowej jest utworzenie wykresu rozrzutu zmiennej odpowiedzi względem zmiennej predykcyjnej.
Na przykład, jeśli utworzymy następujący wykres rozrzutu, zobaczymy, że związek między dwiema zmiennymi jest w przybliżeniu liniowy, więc prosta regresja liniowa prawdopodobnie dobrze sprawdzi się w przypadku tych danych.
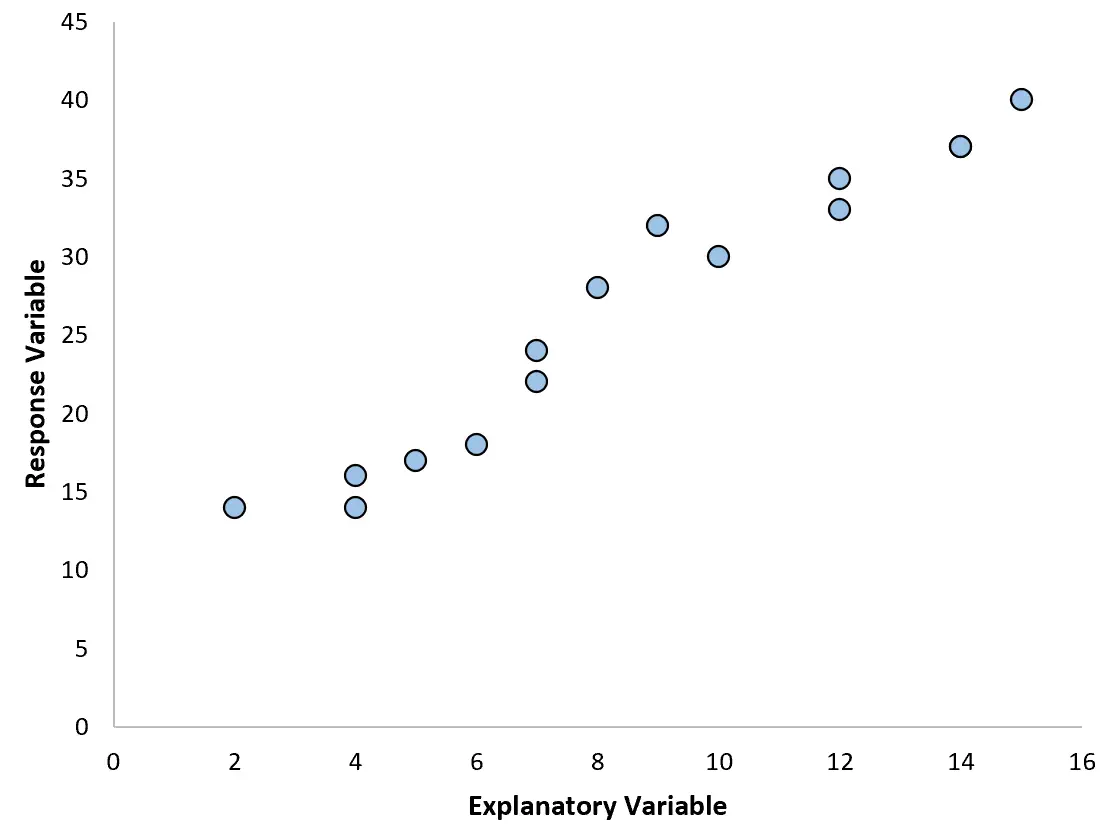
Jeśli jednak nasz wykres rozrzutu wygląda jak jeden z poniższych wykresów, możemy zauważyć, że zależność jest nieliniowa i dlatego dobrym pomysłem byłaby regresja wielomianowa:
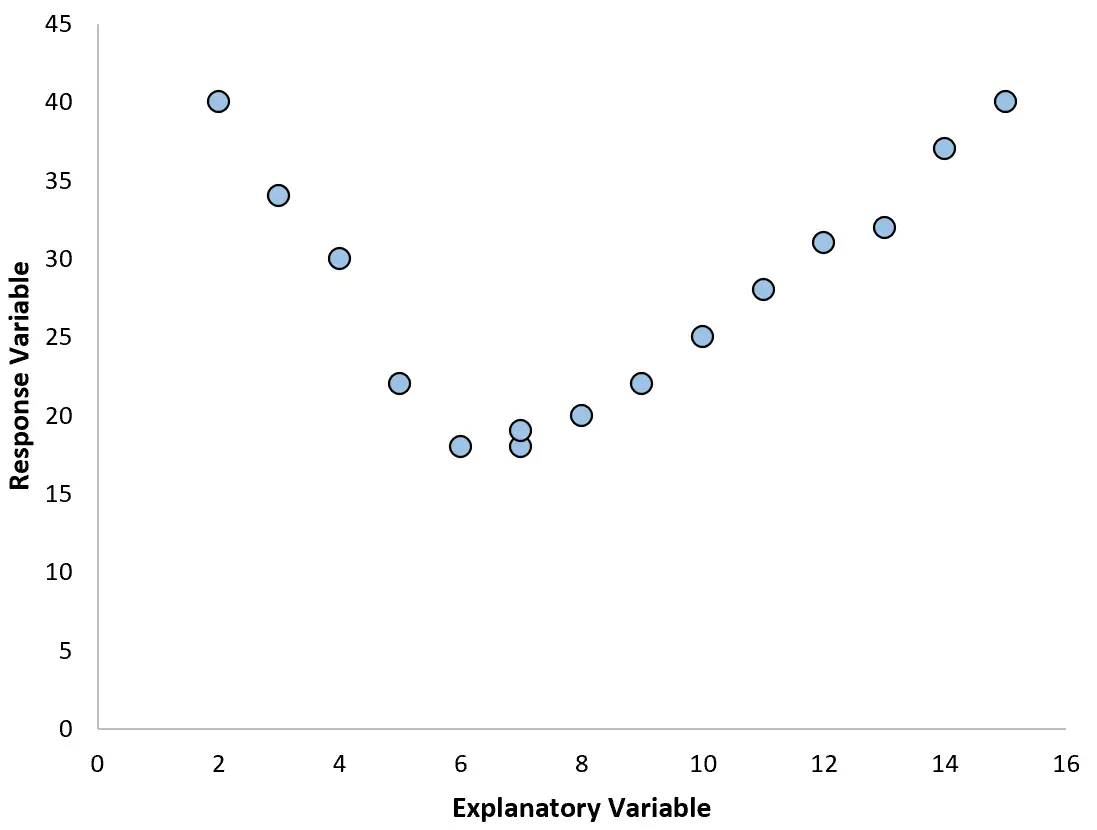
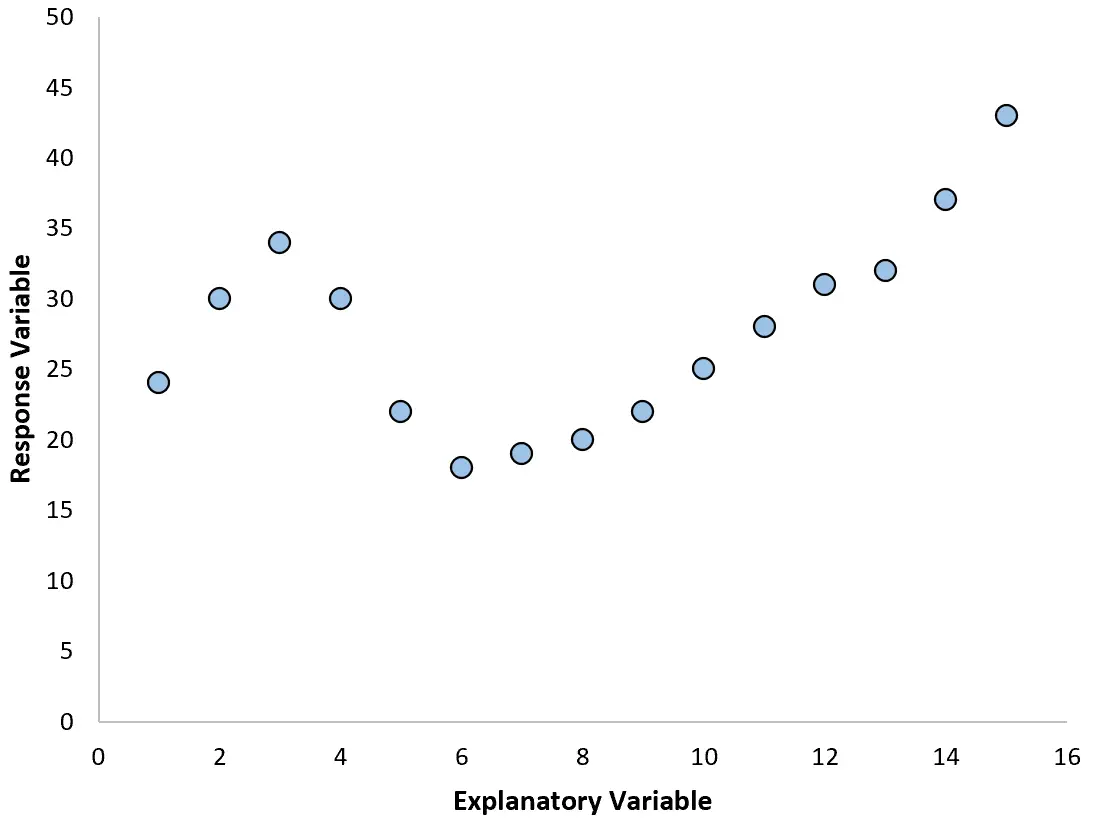
2. Utwórz wykres reszt względem dopasowanego wykresu.
Innym sposobem wykrycia nieliniowości jest dopasowanie do danych prostego modelu regresji liniowej, a następnie utworzenie wykresu reszt w funkcji dopasowanych wartości .
Jeśli reszty na wykresie rozkładają się w przybliżeniu równomiernie wokół zera, bez wyraźnego trendu, wówczas prawdopodobnie wystarczy prosta regresja liniowa.
Jeśli jednak reszty wykazują na wykresie trend nieliniowy, oznacza to, że związek między predyktorem a odpowiedzią jest prawdopodobnie nieliniowy.
3. Oblicz R 2 modelu.
Wartość R 2 modelu regresji wskazuje procent zmienności zmiennej odpowiedzi, który można wyjaśnić za pomocą zmiennych predykcyjnych.
Jeśli do zbioru danych dopasujesz prosty model regresji liniowej, a wartość R 2 modelu jest dość niska, może to wskazywać, że związek między predyktorem a zmienną odpowiedzi jest bardziej złożony niż prosta zależność liniowa.
Może to oznaczać, że zamiast tego konieczne będzie wypróbowanie regresji wielomianowej.
Powiązane: Jaka jest dobra wartość R-kwadrat?
Jak wybrać stopień wielomianu
Model regresji wielomianowej ma następującą postać:
Y = β 0 + β 1 X + β 2 X 2 + … + β godz
W tym równaniu h jest stopniem wielomianu.
Ale jak wybrać wartość h ?
W praktyce dopasowujemy kilka różnych modeli o różnych wartościach h i przeprowadzamy k-krotną walidację krzyżową , aby określić, który model daje najniższy testowy błąd średniokwadratowy (MSE).
Do danego zbioru danych możemy na przykład dopasować następujące modele:
- Y = β 0 + β 1
- Y = β 0 + β 1 X + β 2 X 2
- Y = β0 + β1X + β2X2 + β3X3
- Y = β 0 + β 1 X + β 2 X 2 + β 3 X 3 + β 4 X 4
Następnie możemy zastosować k-krotną walidację krzyżową, aby obliczyć test MSE dla każdego modelu, który powie nam, jak dobrze każdy model radzi sobie z danymi, których nigdy wcześniej nie widział.
Kompromis odchylenia i wariancji w regresji wielomianowej
Podczas stosowania regresji wielomianowej istnieje kompromis w postaci odchylenia wariancji . W miarę zwiększania stopnia wielomianu odchylenie maleje (w miarę jak model staje się bardziej elastyczny), ale wariancja wzrasta.
Podobnie jak w przypadku wszystkich modeli uczenia maszynowego, musimy znaleźć optymalny kompromis między obciążeniem a wariancją.
W większości przypadków pozwala to w pewnym stopniu zwiększyć stopień wielomianu, ale powyżej pewnej wartości model zaczyna dostosowywać się do szumu danych i MSE testu zaczyna spadać.
Aby mieć pewność, że dopasujemy model, który jest elastyczny, ale niezbyt elastyczny, stosujemy k-krotną walidację krzyżową, aby znaleźć model, który daje najniższy test MSE.
Jak przeprowadzić regresję wielomianową
Poniższe samouczki zawierają przykłady przeprowadzania regresji wielomianowej w innym oprogramowaniu:
Jak wykonać regresję wielomianową w programie Excel
Jak wykonać regresję wielomianową w R
Jak wykonać regresję wielomianową w Pythonie
o autorze
Dr Benjamin Anderson
Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej