Wielowymiarowe krzywe regresji adaptacyjnej w r

Wielowymiarowe krzywe regresji adaptacyjnej (MARS) można wykorzystać do modelowania nieliniowych relacji między zestawem zmiennych predykcyjnych a zmienną odpowiedzi .

Ta metoda działa w następujący sposób:

1. Podziel zbiór danych na k części.

2. Dopasuj model regresji do każdej części.

3. Użyj k-krotnej walidacji krzyżowej, aby wybrać wartość k .

W tym samouczku przedstawiono krok po kroku przykład dopasowania modelu MARS do zbioru danych w języku R.

Krok 1: Załaduj niezbędne pakiety

W tym przykładzie użyjemy zbioru danych ISLR Wage .   pakiet zawierający roczne wynagrodzenia 3000 osób wraz z różnymi zmiennymi predykcyjnymi, takimi jak wiek, wykształcenie, rasa i inne.

Przed dopasowaniem modelu MARS do danych załadujemy niezbędne pakiety:

 library (ISLR) #contains Wage dataset
library (dplyr) #data wrangling
library (ggplot2) #plotting
library (earth) #fitting MARS models
library (caret) #tuning model parameters

Krok 2: Wyświetl dane

Następnie wyświetlimy pierwsze sześć wierszy zbioru danych, z którym pracujemy:

 #view first six rows of data
head (Wage)

       year age maritl race education region
231655 2006 18 1. Never Married 1. White 1. < HS Grad 2. Middle Atlantic
86582 2004 24 1. Never Married 1. White 4. College Grad 2. Middle Atlantic
161300 2003 45 2. Married 1. White 3. Some College 2. Middle Atlantic
155159 2003 43 2. Married 3. Asian 4. College Grad 2. Middle Atlantic
11443 2005 50 4. Divorced 1. White 2. HS Grad 2. Middle Atlantic
376662 2008 54 2. Married 1. White 4. College Grad 2. Middle Atlantic
             jobclass health health_ins logwage wage
231655 1. Industrial 1. <=Good 2. No 4.318063 75.04315
86582 2. Information 2. >=Very Good 2. No 4.255273 70.47602
161300 1. Industrial 1. <=Good 1. Yes 4.875061 130.98218
155159 2. Information 2. >=Very Good 1. Yes 5.041393 154.68529
11443 2. Information 1. <=Good 1. Yes 4.318063 75.04315
376662 2. Information 2. >=Very Good 1. Yes 4.845098 127.11574

Krok 3: Utwórz i zoptymalizuj model MARS

Następnie utworzymy model MARS dla tego zbioru danych i przeprowadzimy k-krotną weryfikację krzyżową , aby określić, który model daje najniższy testowy RMSE (średni błąd kwadratowy).

 #create a tuning grid
hyper_grid <- expand. grid (degree = 1:3,
                          nprune = seq (2, 50, length.out = 10) %>%
floor ())

#make this example reproducible
set.seed(1)

#fit MARS model using k-fold cross-validation
cv_mars <- train(
  x = subset(Wage, select = -c(wage, logwage)),
  y = Wage$wage,
  method = " earth ",
  metric = " RMSE ",
  trControl = trainControl(method = " cv ", number = 10),
  tuneGrid = hyper_grid)

#display model with lowest test RMSE
cv_mars$results %>%
  filter (nprune==cv_mars$bestTune$nprune, degree =cv_mars$bestTune$degree)    
degree nprune RMSE Rsquared MAE RMSESD RsquaredSD MAESD		
1 12 33.8164 0.3431804 22.97108 2.240394 0.03064269 1.4554

Z wyników widać, że model, który dał najniższy test MSE, był modelem z jedynie efektami pierwszego rzędu (tj. bez składników interakcji) i 12 składnikami. Model ten dał średni błąd kwadratowy (RMSE) wynoszący 33,8164 .

Uwaga: Użyliśmy metody = „earth”, aby określić model MARS. Dokumentację tej metody można znaleźć tutaj .

Możemy również utworzyć wykres wizualizujący test RMSE na podstawie stopnia i liczby terminów:

 #display test RMSE by terms and degree
ggplot(cv_mars)

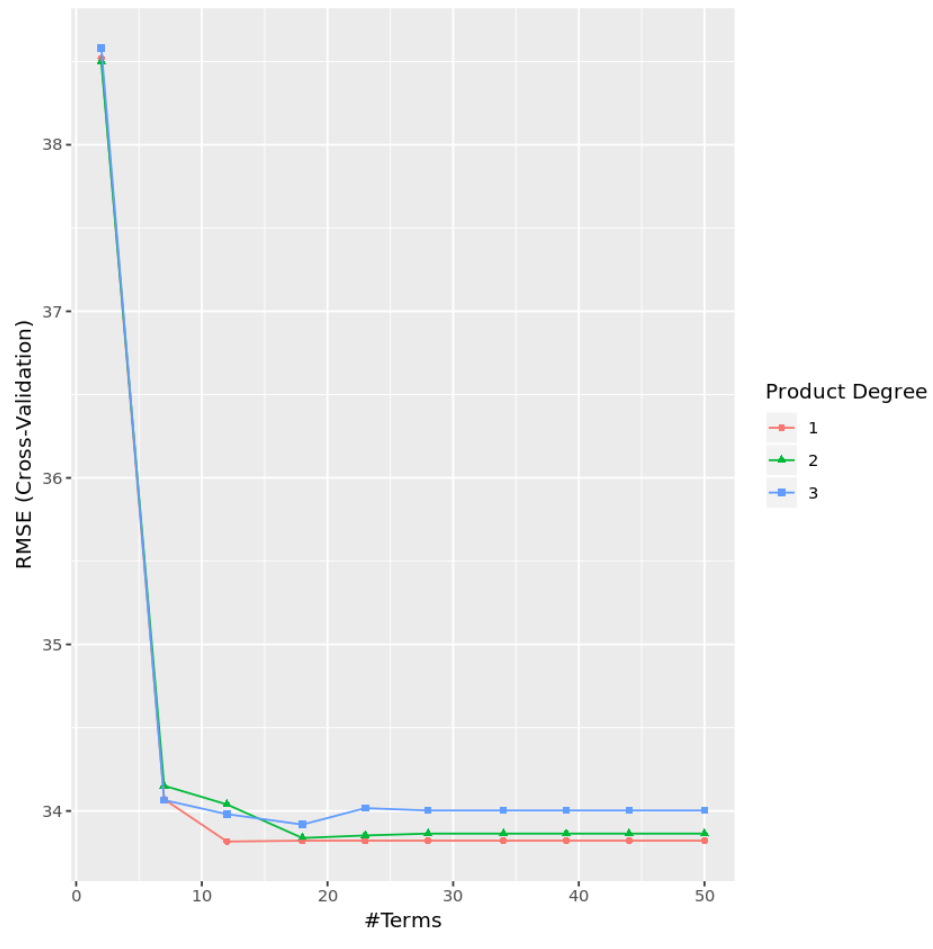
W praktyce dostosowalibyśmy model MARS do kilku innych typów modeli, takich jak:

• Wielokrotna regresja liniowa
• Regresja wielomianowa
• Regresja szczytowa
• Regresja Lassa
• Regresja głównych składników
• Częściowe metody najmniejszych kwadratów

Następnie porównalibyśmy każdy model, aby określić, który prowadzi do najmniejszego błędu testu i wybrać ten model jako optymalny do użycia.

Pełny kod R użyty w tym przykładzie można znaleźć tutaj .