Pourquoi les statistiques sont-elles importantes ? (10 raisons pour lesquelles les statistiques sont importantes !)

Le domaine des statistiques concerne la collecte, l’analyse, l’interprétation et la présentation des données.

Alors que la technologie devient de plus en plus présente dans notre vie quotidienne, davantage de données sont générées et collectées que jamais dans l’histoire de l’humanité.

Les statistiques sont le domaine qui peut nous aider à comprendre comment utiliser ces données pour effectuer les tâches suivantes :

• Mieux comprendre le monde qui nous entoure.
• Prenez des décisions en utilisant les données.
• Faites des prédictions sur l’avenir à l’aide de données.

Dans cet article, nous partageons 10 raisons pour lesquelles le domaine des statistiques est si important dans la vie moderne.

Raison 1 : Utiliser les statistiques descriptives pour comprendre le monde

Les statistiques descriptives sont utilisées pour décrire un morceau de données brutes. Il existe trois principaux types de statistiques descriptives :

• Statistiques récapitulatives
• Graphiques
• les tables

Chacun de ces éléments peut nous aider à mieux comprendre les données existantes.

Par exemple, supposons que nous disposions d’un ensemble de données brutes montrant les résultats aux tests de 10 000 étudiants dans une certaine ville. Nous pouvons utiliser des statistiques descriptives pour :

• Calculez la note moyenne du test et l’écart type des résultats du test.
• Générez un histogramme ou un boxplot pour visualiser la distribution des résultats des tests.
• Créez un tableau de fréquence pour comprendre la distribution des résultats des tests.

En utilisant des statistiques descriptives, nous pouvons comprendre les résultats des tests des étudiants beaucoup plus facilement qu’en regardant simplement les données brutes.

Raison 2 : se méfier des graphiques trompeurs

De plus en plus de graphiques sont générés dans les revues, les médias, les articles en ligne et les magazines. Malheureusement, les graphiques peuvent souvent être trompeurs si vous ne comprenez pas les données sous-jacentes.

Par exemple, supposons qu’une revue publie une étude qui révèle une corrélation négative entre les scores GPA et ACT des étudiants d’une certaine université.

Cependant, cette corrélation négative ne se produit que parce que les étudiants qui ont à la fois un score GPA et ACT élevés peuvent fréquenter une université d’élite, tandis que les étudiants qui ont à la fois un score GPA et ACT faibles ne sont pas admis du tout.

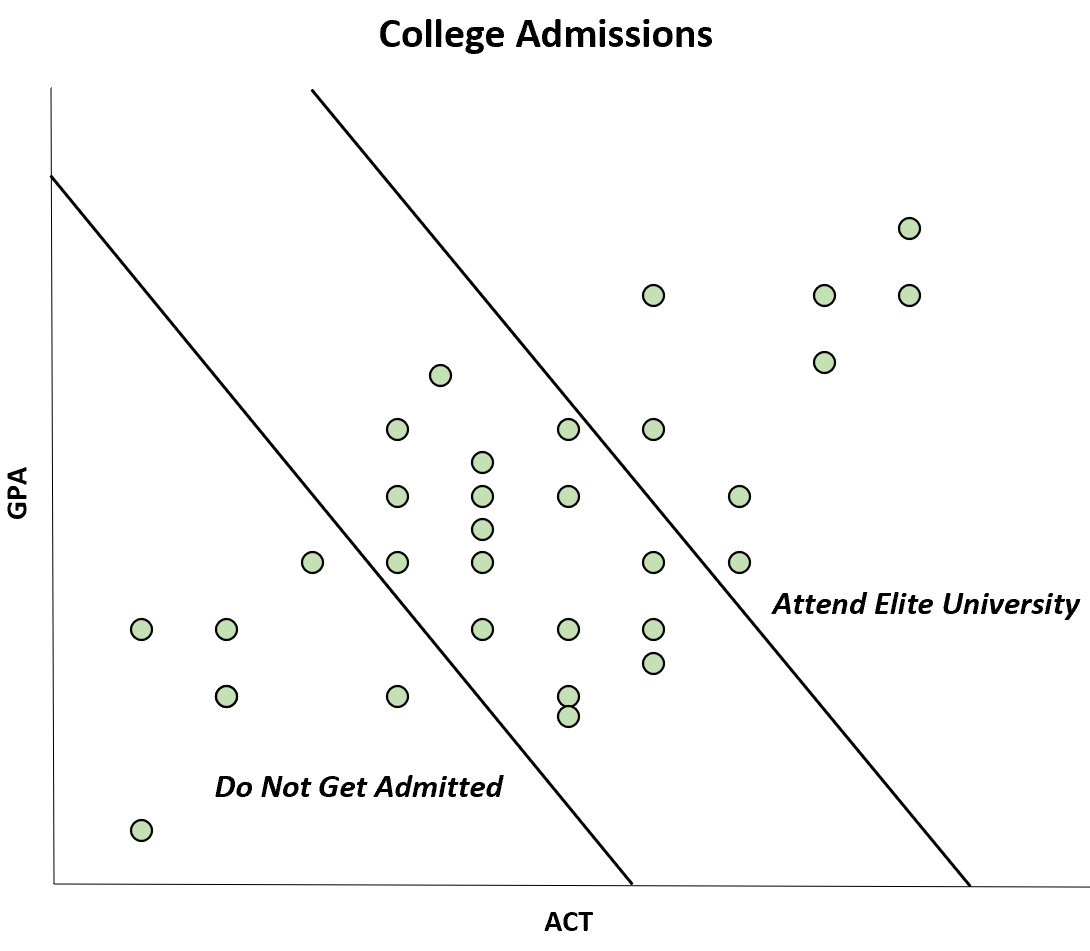
Bien que la corrélation entre ACT et GPA soit positive dans la population, la corrélation semble négative dans l’échantillon.

Ce biais particulier est connu sous le nom de biais de Berkson . En étant conscient de ce biais, vous pouvez éviter de vous laisser induire en erreur par certains graphiques.

Raison 3 : se méfier des variables confondantes

Un concept important que vous découvrirez en statistiques est le concept de variables confondantes .

Ce sont des variables qui ne sont pas prises en compte et qui peuvent confondre les résultats d’une expérience et conduire à des conclusions peu fiables.

Par exemple, supposons qu’un chercheur collecte des données sur les ventes de glaces et les attaques de requins et découvre que les deux variables sont fortement corrélées. Cela signifie-t-il que l’augmentation des ventes de glaces provoque davantage d’attaques de requins ?

C’est peu probable. La cause la plus probable est la température variable confondante. Quand il fait plus chaud dehors, plus de gens achètent des glaces et plus de gens vont dans l’océan.

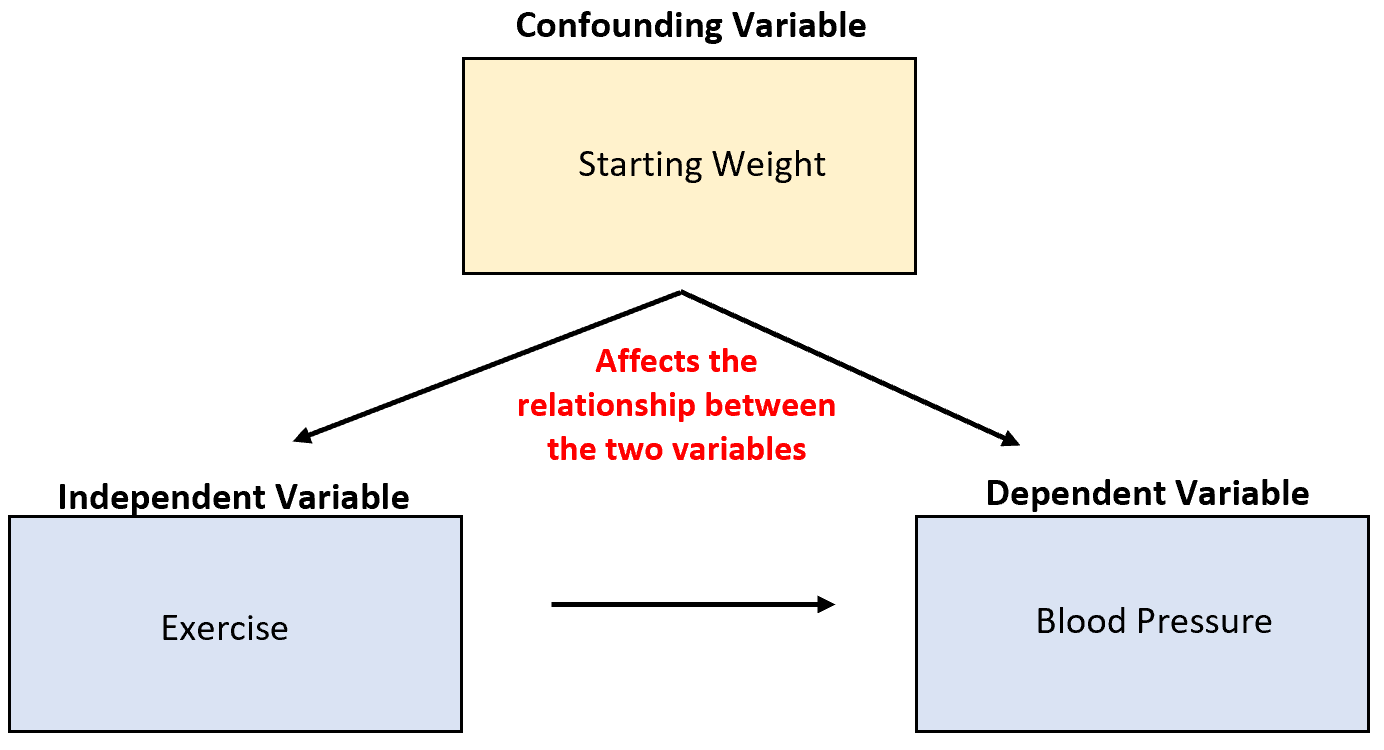
Raison 4 : pour prendre de meilleures décisions en utilisant les probabilités

L’un des sous-domaines les plus importants des statistiques est la probabilité . C’est le domaine qui étudie la probabilité que les événements se produisent.

En ayant une compréhension de base des probabilités, vous pouvez prendre des décisions plus éclairées dans le monde réel.

Par exemple, supposons qu’un lycéen sache qu’il a 10 % de chances d’être accepté dans une université donnée. En utilisant la formule de la probabilité de réussite « d’au moins un » , cet étudiant peut trouver la probabilité qu’il soit accepté dans au moins une université pour laquelle il postule et peut ajuster le nombre d’universités pour lesquelles il postule en conséquence.

Raison 5 : Comprendre les valeurs P dans la recherche

Un autre concept important que vous découvrirez en statistiques est celui des valeurs p .

La définition classique d’une valeur p est la suivante :

Une valeur p est la probabilité d’observer une statistique d’échantillon qui est au moins aussi extrême que la statistique de votre échantillon, étant donné que l’hypothèse nulle est vraie.

Par exemple, supposons qu’une usine prétende produire des pneus d’un poids moyen de 200 livres. Un auditeur émet l’hypothèse que le poids moyen réel des pneus produits dans cette usine est différent de 200 livres. Il effectue donc un test d’hypothèse et constate que la valeur p du test est de 0,04.

Voici comment interpréter cette valeur p :

Si l’usine produit effectivement des pneus d’un poids moyen de 200 livres, alors 4 % de tous les audits obtiendront l’effet observé dans l’échantillon, ou plus, en raison d’une erreur d’échantillonnage aléatoire. Cela nous indique que l’obtention des échantillons de données obtenus par l’auditeur serait assez rare si l’usine produisait effectivement des pneus d’un poids moyen de 200 livres.

Ainsi, l’auditeur rejetterait probablement l’hypothèse nulle selon laquelle le poids moyen réel des pneus produits dans cette usine est effectivement de 200 livres.

Raison 6 : Comprendre la corrélation

Un autre concept important que vous découvrirez en statistiques est la corrélation , qui nous indique l’association linéaire entre deux variables.

La valeur d’un coefficient de corrélation est toujours comprise entre -1 et 1 où :

• -1 indique une corrélation linéaire parfaitement négative entre deux variables
• 0 indique aucune corrélation linéaire entre deux variables
• 1 indique une corrélation linéaire parfaitement positive entre deux variables

En comprenant ces valeurs, vous pouvez comprendre la relation entre les variables dans le monde réel.

Par exemple, si la corrélation entre les dépenses publicitaires et les revenus est de 0,87, vous pouvez alors comprendre qu’il existe une forte relation positive entre les deux variables. À mesure que vous dépensez plus d’argent en publicité, vous pouvez vous attendre à une augmentation prévisible de vos revenus.

Raison 7 : Faire des prédictions sur l’avenir

Une autre raison importante d’apprendre les statistiques est de comprendre les modèles de régression de base tels que :

• Régression linéaire simple
• La régression linéaire multiple
• Régression logistique

Chacun de ces modèles vous permet de faire des prédictions sur la valeur future d’une variable de réponse en fonction de la valeur de certaines variables prédictives du modèle.

Par exemple, les entreprises utilisent constamment des modèles de régression linéaire multiples dans le monde réel lorsqu’elles utilisent des variables prédictives telles que l’âge, le revenu, l’origine ethnique, etc. pour prédire combien les clients dépenseront dans leurs magasins.

De même, les entreprises de logistique utilisent des variables prédictives telles que la demande totale, la taille de la population, etc. pour prévoir les ventes futures.

Quel que soit le domaine dans lequel vous travaillez, il y a de fortes chances que des modèles de régression soient utilisés pour prédire un phénomène futur.

Raison 8 : Comprendre les biais potentiels dans les études

Une autre raison d’étudier les statistiques est d’être conscient de tous les différents types de biais qui peuvent survenir dans les études du monde réel.

Voici quelques exemples :

• Biais de l’observateur
• Biais d’autosélection
• Biais de référence
• Biais variable omis
• Biais de sous-dénombrement
• Biais de non-réponse

En ayant une compréhension de base de ces types de préjugés, vous pouvez éviter de les commettre lorsque vous effectuez des recherches ou en être conscient lorsque vous lisez d’autres documents de recherche ou études.

Raison 9 : Comprendre les hypothèses formulées par les tests statistiques

De nombreux tests statistiques émettent des hypothèses sur les données sous-jacentes étudiées.

Lorsque vous lisez les résultats d’une étude ou même lorsque vous réalisez votre propre étude, il est important de comprendre quelles hypothèses doivent être formulées pour que les résultats soient fiables.

Les articles suivants partagent les hypothèses formulées dans de nombreux tests et procédures statistiques couramment utilisés :

• Qu’est-ce que l’hypothèse d’une variance égale dans les statistiques ?
• Qu’est-ce que l’hypothèse de normalité en statistique ?
• Qu’est-ce que l’hypothèse d’indépendance dans les statistiques ?

Raison 10 : Pour éviter une généralisation excessive

Une autre raison d’étudier les statistiques est de comprendre le concept de généralisation excessive .

Cela se produit lorsque les individus participant à une étude ne sont pas représentatifs des individus de la population globale et qu’il est donc inapproprié de généraliser les conclusions d’une étude à l’ensemble de la population.

Par exemple, supposons que nous voulions savoir quel pourcentage d’élèves d’une certaine école préfèrent le « drame » comme genre de film préféré. Si la population étudiante totale est un mélange de 50 % de garçons et 50 % de filles, alors un échantillon composé de 90 % de garçons et de 10 % de filles pourrait conduire à des résultats biaisés si beaucoup moins de garçons préfèrent le théâtre comme genre préféré.

Idéalement, nous voulons que notre échantillon ressemble à une « mini-version » de notre population. Ainsi, si la population étudiante globale est composée de 50 % de filles et 50 % de garçons, notre échantillon ne serait pas représentatif s’il comprenait 90 % de garçons et seulement 10 % de filles.

Ainsi, que vous meniez votre propre enquête ou que vous lisiez les résultats d’une enquête, il est important de comprendre si les données de l’échantillon sont représentatives de la population totale et si les résultats de l’enquête peuvent être généralisés à la population avec confiance.

Ressources additionnelles

Consultez les articles suivants pour acquérir une compréhension de base des concepts les plus importants en matière de statistiques d’introduction :

Statistiques descriptives ou inférentielles
Population vs échantillon
Statistique vs paramètre
Variables qualitatives et quantitatives
Niveaux de mesure : nominal, ordinal, intervalle et rapport