Qu’est-ce qu’une variable confusionnelle ? (Définition & #038; Exemple)

Dans toute expérience, il y a deux variables principales :

La variable indépendante : la variable qu’un expérimentateur modifie ou contrôle afin de pouvoir observer les effets sur la variable dépendante.

La variable dépendante : la variable mesurée dans une expérience qui est « dépendante » de la variable indépendante.

Les chercheurs souhaitent souvent comprendre comment les changements dans la variable indépendante affectent la variable dépendante.

Cependant, il arrive parfois qu’une troisième variable ne soit pas prise en compte et qu’elle puisse affecter la relation entre les deux variables étudiées.

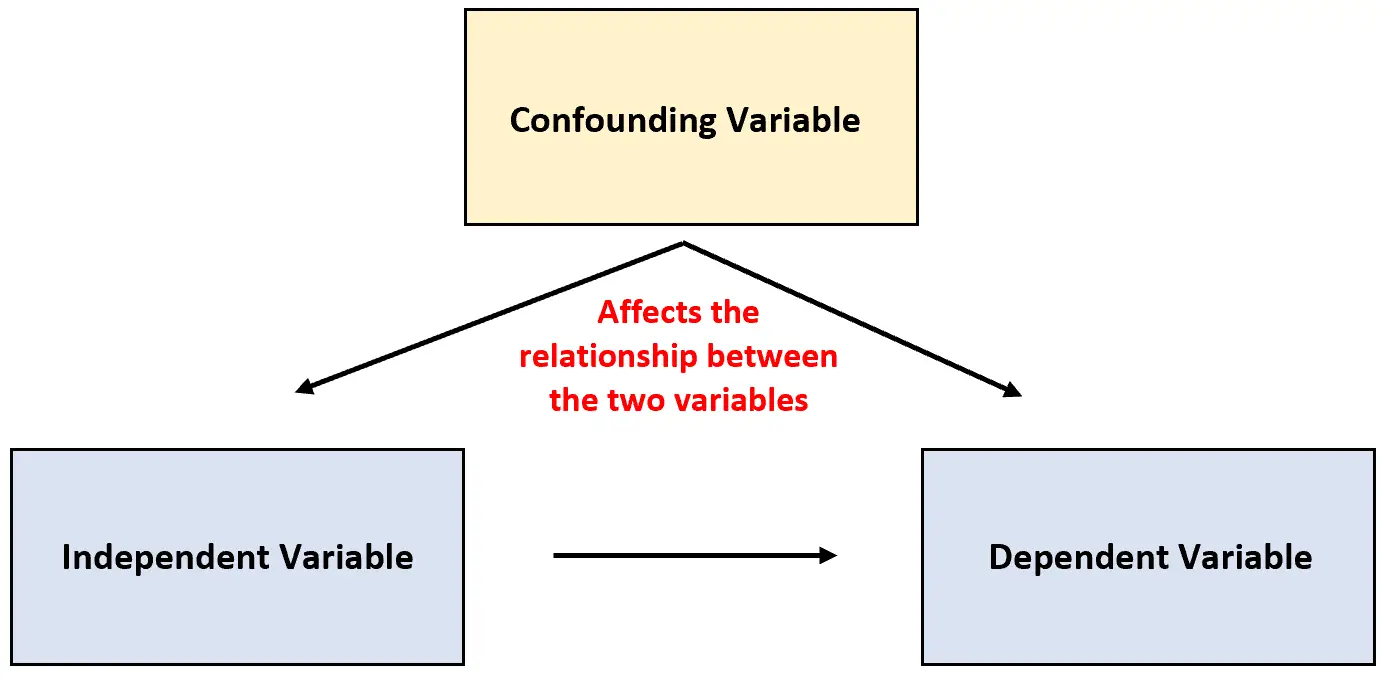
Ce type de variable est connu sous le nom de variable confondante et peut confondre les résultats d’une étude et donner l’impression qu’il existe un certain type de relation de cause à effet entre deux variables qui n’existe pas réellement.

Variable confondante : variable qui n’est pas incluse dans une expérience, mais qui affecte la relation entre les deux variables d’une expérience.

Ce type de variable peut confondre les résultats d’une expérience et conduire à des résultats peu fiables.

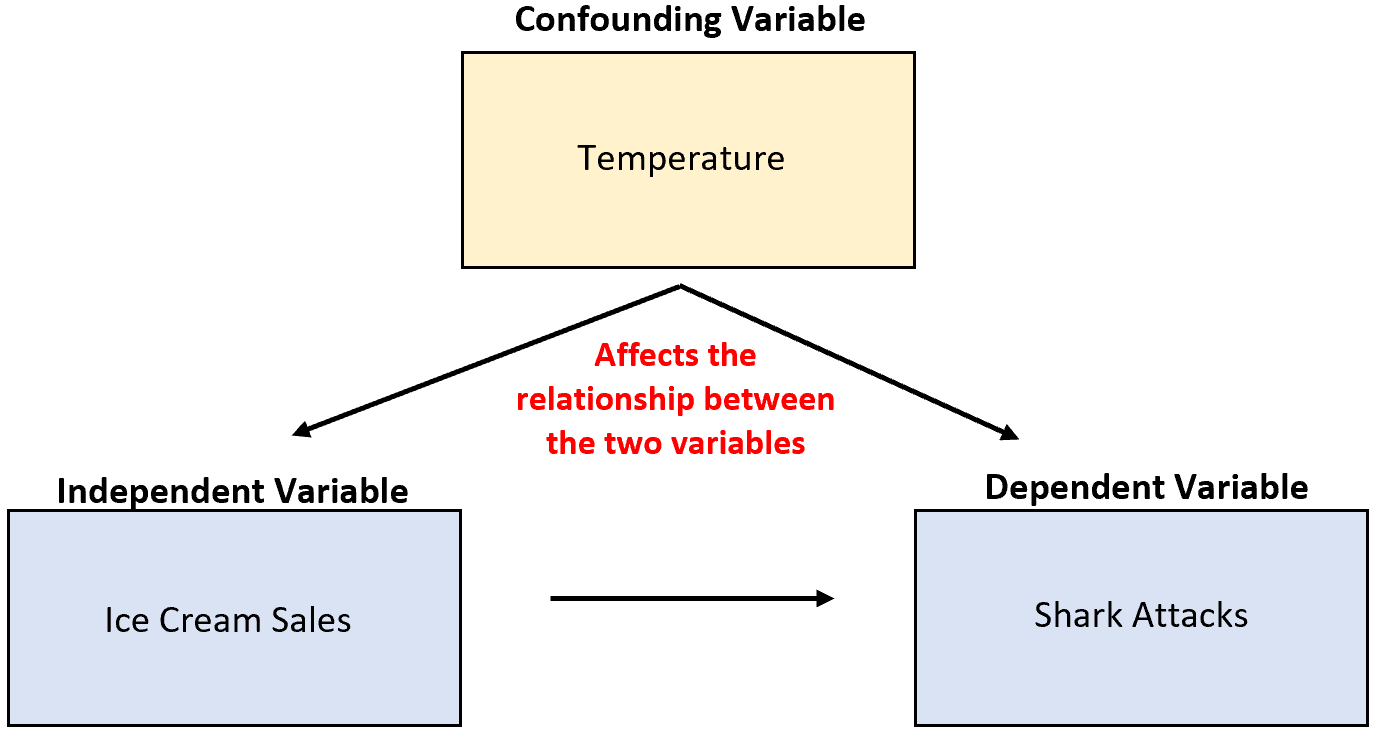
Par exemple, supposons qu’un chercheur collecte des données sur les ventes de glaces et les attaques de requins et découvre que les deux variables sont fortement corrélées. Cela signifie-t-il que l’augmentation des ventes de glaces provoque davantage d’attaques de requins ?

C’est peu probable. La cause la plus probable est la température variable confondante. Quand il fait plus chaud dehors, plus de gens achètent des glaces et plus de gens vont dans l’océan.

Conditions requises pour les variables confusionnelles

Pour qu’une variable soit une variable de confusion, elle doit répondre aux exigences suivantes :

1. Elle doit être corrélée à la variable indépendante.

Dans l’exemple précédent, la température était corrélée à la variable indépendante des ventes de glaces. En particulier, des températures plus chaudes sont associées à des ventes de crème glacée plus élevées et des températures plus froides à des ventes plus faibles.

2. Il doit y avoir une relation causale avec la variable dépendante.

Dans l’exemple précédent, la température avait un effet causal direct sur le nombre d’attaques de requins. En particulier, des températures plus chaudes poussent davantage de personnes à se rendre dans l’océan, ce qui augmente directement la probabilité d’attaques de requins.

Pourquoi les variables confusionnelles sont-elles problématiques ?

Les variables confusionnelles sont problématiques pour deux raisons :

1. Des variables confusionnelles peuvent donner l’impression que des relations de cause à effet existent alors qu’elles n’existent pas.

Dans notre exemple précédent, la variable confusionnelle de la température donnait l’impression qu’il existait une relation de cause à effet entre les ventes de glaces et les attaques de requins.

Or, on sait que la vente de glaces ne provoque pas d’attaques de requins. La variable confondante de la température donne l’impression que c’est ainsi.

2. Les variables confusionnelles peuvent masquer la véritable relation de cause à effet entre les variables.

Supposons que nous étudions la capacité de l’exercice à réduire la tension artérielle. Une variable confondante potentielle est le poids de départ, qui est corrélé à l’exercice et a un effet causal direct sur la tension artérielle.

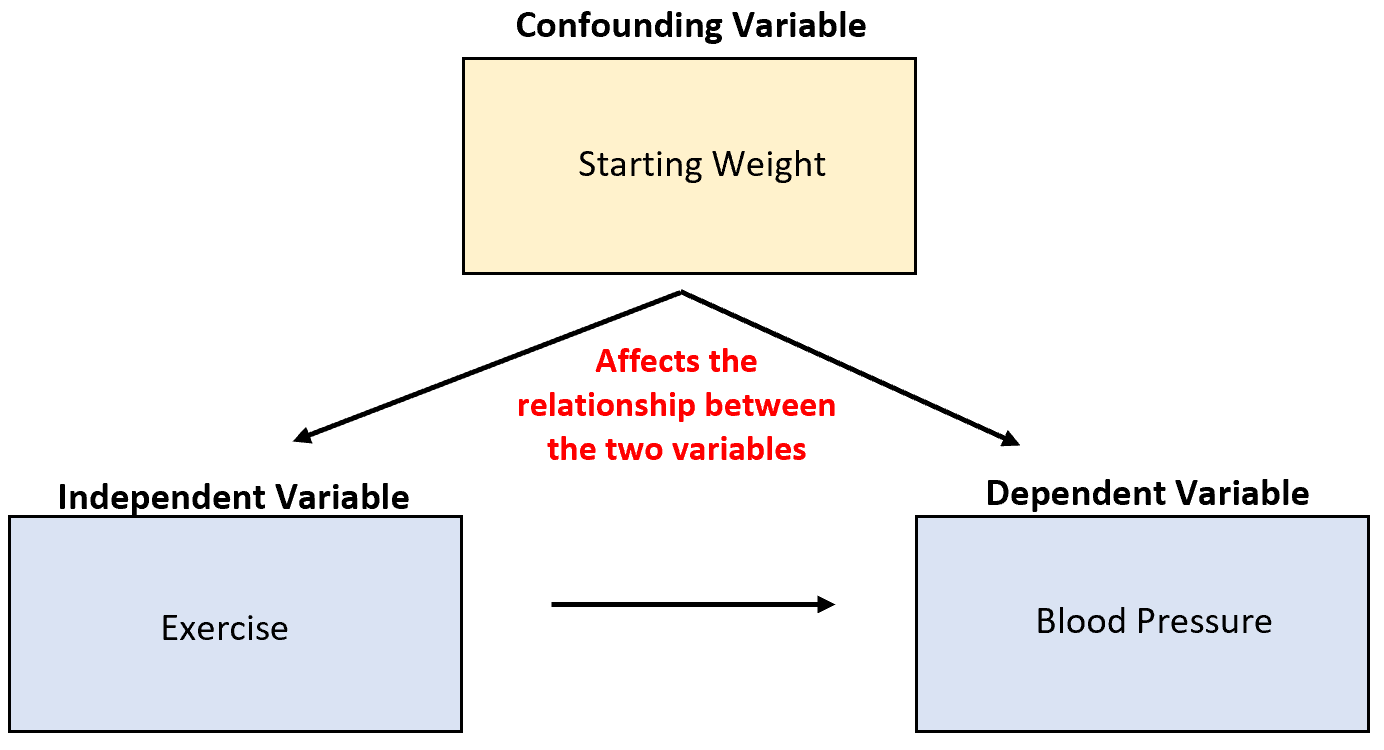
Bien qu’une activité physique accrue puisse entraîner une réduction de la tension artérielle, le poids de départ d’un individu a également un impact important sur la relation entre ces deux variables.

Variables confondantes et validité interne

En termes techniques, les variables confondantes affectent la validité interne d’une étude, qui fait référence à la validité d’attribuer tout changement dans la variable dépendante aux changements dans la variable indépendante.

Lorsque des variables confusionnelles sont présentes, nous ne pouvons pas toujours affirmer avec certitude que les changements que nous observons dans la variable dépendante sont le résultat direct des changements dans la variable indépendante.

Comment réduire l’effet des variables confusionnelles

Il existe plusieurs façons de réduire l’effet des variables confondantes, notamment les méthodes suivantes :

1. Attribution aléatoire

L’assignation aléatoire fait référence au processus d’affectation aléatoire des individus d’une étude à un groupe de traitement ou à un groupe témoin.

Par exemple, supposons que nous souhaitions étudier l’effet d’une nouvelle pilule sur la tension artérielle. Si nous recrutons 100 personnes pour participer à l’étude, nous pourrions utiliser un générateur de nombres aléatoires pour attribuer au hasard 50 personnes à un groupe témoin (pas de pilule) et 50 personnes à un groupe de traitement (nouvelle pilule).

En utilisant l’assignation aléatoire, nous augmentons les chances que les deux groupes aient des caractéristiques à peu près similaires, ce qui signifie que toute différence observée entre les deux groupes peut être attribuée au traitement.

Cela signifie que l’étude doit avoir une validité interne : il est valable d’attribuer toute différence de tension artérielle entre les groupes à la pilule elle-même, par opposition aux différences entre les individus des groupes.

2. Blocage

Le blocage fait référence à la pratique consistant à diviser les individus dans une étude en « blocs » en fonction d’une certaine valeur d’une variable de confusion afin d’éliminer l’effet de la variable de confusion.

Par exemple, supposons que les chercheurs souhaitent comprendre l’effet d’un nouveau régime sur la perte de poids. La variable indépendante est le nouveau régime alimentaire et la variable dépendante est le montant de la perte de poids.

Cependant, une variable confondante susceptible d’entraîner une variation de la perte de poids est le sexe . Il est probable que le sexe d’un individu aura une incidence sur la quantité de poids qu’il perdra, que le nouveau régime fonctionne ou non.

Une façon de résoudre ce problème consiste à placer les individus dans l’un des deux blocs suivants :

• Mâle
• Femelle

Ensuite, au sein de chaque bloc, nous assignerions au hasard les individus à l’un des deux traitements suivants :

• Un nouveau régime
• Un régime standard

En faisant cela, la variation au sein de chaque bloc serait bien inférieure à la variation entre tous les individus et nous serions en mesure de mieux comprendre comment le nouveau régime affecte la perte de poids tout en contrôlant le sexe.

3. Correspondance

Un plan par paires appariées est un type de plan expérimental dans lequel nous « faisons correspondre » des individus en fonction des valeurs de variables confusionnelles potentielles.

Par exemple, supposons que les chercheurs souhaitent savoir comment un nouveau régime affecte la perte de poids par rapport à un régime standard. Deux variables confusionnelles potentielles dans cette situation sont l’âge et le sexe .

Pour tenir compte de cela, les chercheurs recrutent 100 sujets, puis les regroupent en 50 paires en fonction de leur âge et de leur sexe. Par exemple:

• Un homme de 25 ans sera jumelé à un autre homme de 25 ans, puisqu’ils « correspondent » en termes d’âge et de sexe.
• Une femme de 30 ans sera jumelée à une autre femme de 30 ans puisqu’elles correspondent également en termes d’âge et de sexe, etc.

Ensuite, au sein de chaque paire, un sujet sera assigné au hasard pour suivre le nouveau régime pendant 30 jours et l’autre sujet sera assigné à suivre le régime standard pendant 30 jours.

À la fin des 30 jours, les chercheurs mesureront la perte de poids totale pour chaque sujet.

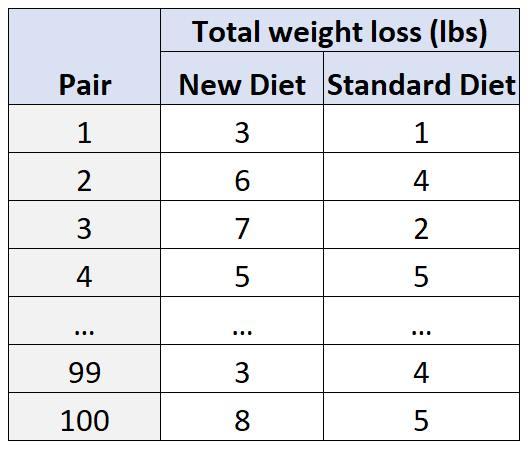
En utilisant ce type de conception, les chercheurs peuvent être sûrs que toute différence dans la perte de poids peut être attribuée au type de régime utilisé plutôt qu’aux variables confondantes que sont l’âge et le sexe .

Ce type de conception présente quelques inconvénients, notamment :

1. Perdre deux matières si l’une d’entre elles abandonne. Si un sujet décide d’abandonner l’étude, vous perdez en réalité deux sujets puisque vous n’avez plus une paire complète.

2. Il faut du temps pour trouver des correspondances . Trouver des sujets qui correspondent à certaines variables, telles que le sexe et l’âge, peut prendre beaucoup de temps.

3. Impossible de faire correspondre parfaitement les sujets . Quels que soient vos efforts, il y aura toujours des variations au sein des sujets de chaque paire.

Cependant, si une étude dispose des ressources disponibles pour mettre en œuvre ce modèle, elle peut être très efficace pour éliminer les effets des variables confondantes.