Proportion de l’échantillon
Cet article explique quelle est la proportion d’échantillon dans les statistiques. Ainsi, vous découvrirez comment calculer la proportion de l’échantillon, un exercice résolu et, également, quelle est la différence entre la proportion de l’échantillon et la proportion de la population.
Quelle est la proportion de l’échantillon ?
La proportion d’échantillon est le rapport des cas réussis dans un échantillon à la taille dudit échantillon. Par conséquent, pour calculer la proportion de l’échantillon, le nombre de réussites dans l’échantillon doit être divisé par le nombre total de données.
Le symbole de la proportion d’échantillon est
![]() .
.
En statistique, lors de la réalisation d’une enquête, toutes les données de la population ne sont généralement pas connues, c’est pourquoi une étude d’un échantillon représentatif est généralement réalisée, puis les conclusions tirées sont extrapolées à l’ensemble de la population. Ainsi, la proportion de l’échantillon sert à estimer la proportion de l’ensemble de la population. Ci-dessous, nous verrons comment cela se fait.
Exemple de formule de proportion
La proportion de l’échantillon est égale au nombre de cas réussis dans l’échantillon divisé par la taille de l’échantillon. Par conséquent, la formule pour calculer la proportion de l’échantillon est la suivante :
![]()
Où:
 est la proportion de l’échantillon.
est la proportion de l’échantillon. est le nombre de cas de réussite dans l’échantillon.
est le nombre de cas de réussite dans l’échantillon. est le nombre total de données dans l’échantillon.
est le nombre total de données dans l’échantillon.
Exemple de calcul de la proportion d’échantillon
Après avoir vu la définition de la proportion d’échantillon et quelle est sa formule, dans cette section, nous allons résoudre un exemple simple afin que vous puissiez voir comment la proportion d’échantillon est calculée.
- Une entreprise fabrique un jouet dont elle achète une de ses pièces à une autre entreprise extérieure. Cependant, au sein des lots qu’il achète, des pièces défectueuses apparaissent, il décide donc de réaliser une étude statistique pour connaître la proportion de pièces en bon état et la proportion de défauts. Ainsi, vous commandez un échantillon de 1 000 unités et trouvez 138 pièces défectueuses. Quelle est la proportion de pièces en bon état dans l’échantillon ? Et quelle est la proportion de pièces défectueuses dans l’échantillon ?
Le nombre de pièces en bon état dans l’échantillon est de 1000 moins le nombre de pièces défectueuses :
![]()
Ainsi, pour trouver la proportion de l’échantillon, nous appliquons la formule que nous avons vue ci-dessus :
![]()
La proportion de l’échantillon de pièces en bon état est donc de 86,2 %.
En revanche, la proportion de pièces défectueuses équivaut à un moins la proportion de pièces bonnes :
![]()
La proportion d’échantillon de pièces défectueuses est donc de 13,8 %.
Proportion de l’échantillon et proportion de la population
La proportion de population est la proportion de la population statistique. C’est-à-dire que la proportion de population est la relation des cas de réussite d’une population étudiée par rapport à tous les éléments qui font partie de ladite population.
Por lo tanto, la diferencia entre la proporción muestral y la proporción poblacional es que la proporción muestral es la proporción de casos de éxitos de una muestra, en cambio, la proporción poblacional se refiere a la proporción de casos de éxitos respecto a todos los elementos de la population.
Pour différencier la proportion d’échantillon de la proportion de population, elles sont représentées par des symboles différents. Le symbole de la proportion d’échantillon est
![]() , tandis que le symbole de la proportion de population est
, tandis que le symbole de la proportion de population est![]() .
.
En général, la proportion de la population ne peut pas être déterminée avec précision, car toutes les valeurs de la population ne sont généralement pas connues. Au lieu de cela, la valeur de la proportion de population est généralement estimée à l’aide d’un intervalle de confiance dont la formule est la suivante :
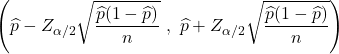
Pour voir comment est faite l’estimation de la proportion de population, cliquez sur le lien suivant :
Distribution d’échantillonnage des proportions
Enfin, nous allons voir en quoi consiste une distribution d’échantillonnage de proportions, puisqu’il s’agit d’un concept statistique lié à la proportion d’échantillonnage.
Tout d’abord, commençons par définir ce qu’est une distribution d’échantillonnage. Une distribution d’échantillonnage est la distribution qui résulte de la prise en compte de tous les échantillons possibles d’une population statistique.
Par conséquent, une distribution d’échantillonnage de proportions est la distribution qui résulte du calcul de la proportion de chaque échantillon possible d’une population. Autrement dit, si nous étudions tous les échantillons possibles d’une population et calculons la proportion de chacun des échantillons, l’ensemble de valeurs calculé est une distribution d’échantillonnage des proportions d’échantillon.
