Comment créer et interpréter des tracés Q-Q dans Stata

Un tracé QQ , abréviation de « quantile-quantile », est souvent utilisé pour évaluer si les résidus d’une analyse de régression sont normalement distribués ou non.

Ce tutoriel explique comment créer et interpréter un tracé QQ dans Stata.

Exemple : tracé QQ dans Stata

Pour cet exemple, nous utiliserons l’ensemble de données automatique intégré dans Stata. Nous ajusterons un modèle de régression linéaire multiple, en utilisant le mpg et le déplacement comme variables explicatives et le prix comme variable de réponse. Nous obtiendrons ensuite les résidus pour le modèle et créerons un tracé QQ pour voir si les résidus suivent une distribution normale.

Étape 1 : Chargez et affichez les données.

Tout d’abord, nous allons charger les données à l’aide de la commande suivante :

utilisation automatique du système

Ensuite, nous obtiendrons un résumé rapide des données à l’aide de la commande suivante :

résumer

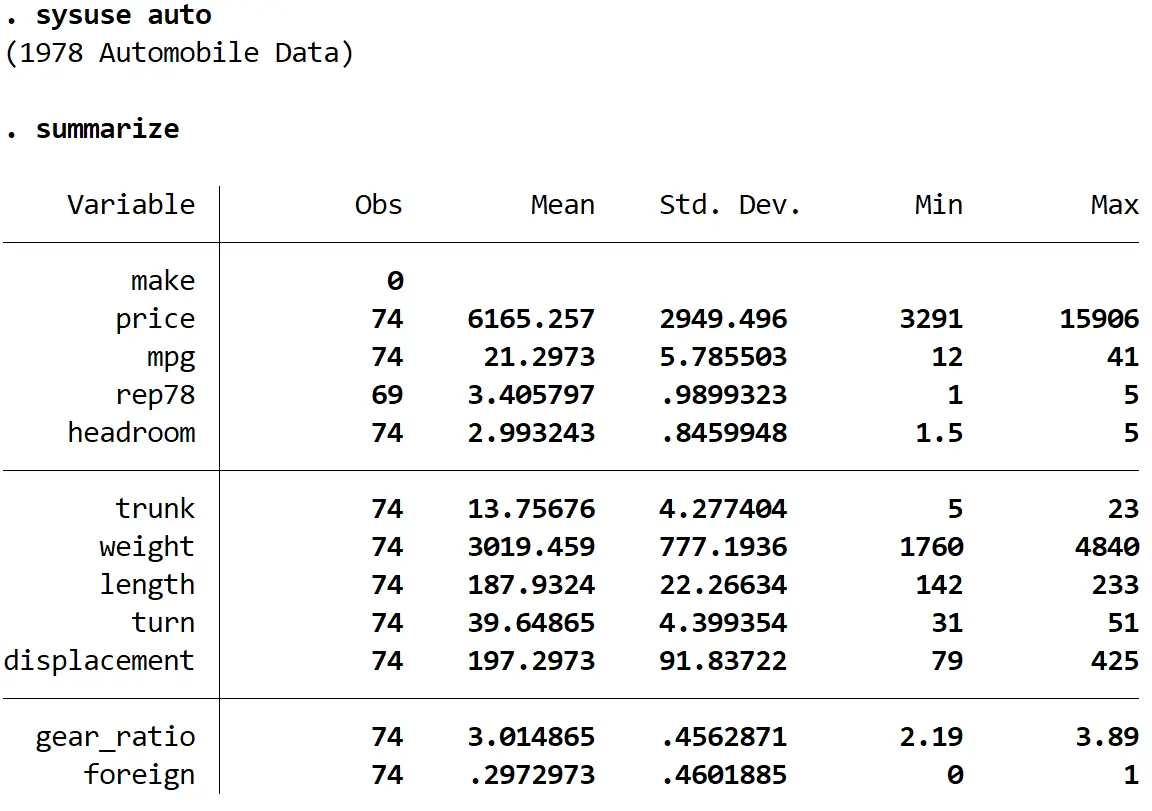
Étape 2 : Ajustez le modèle de régression.

Ensuite, nous utiliserons la commande suivante pour ajuster le modèle de régression :

régression prix mpg déplacement

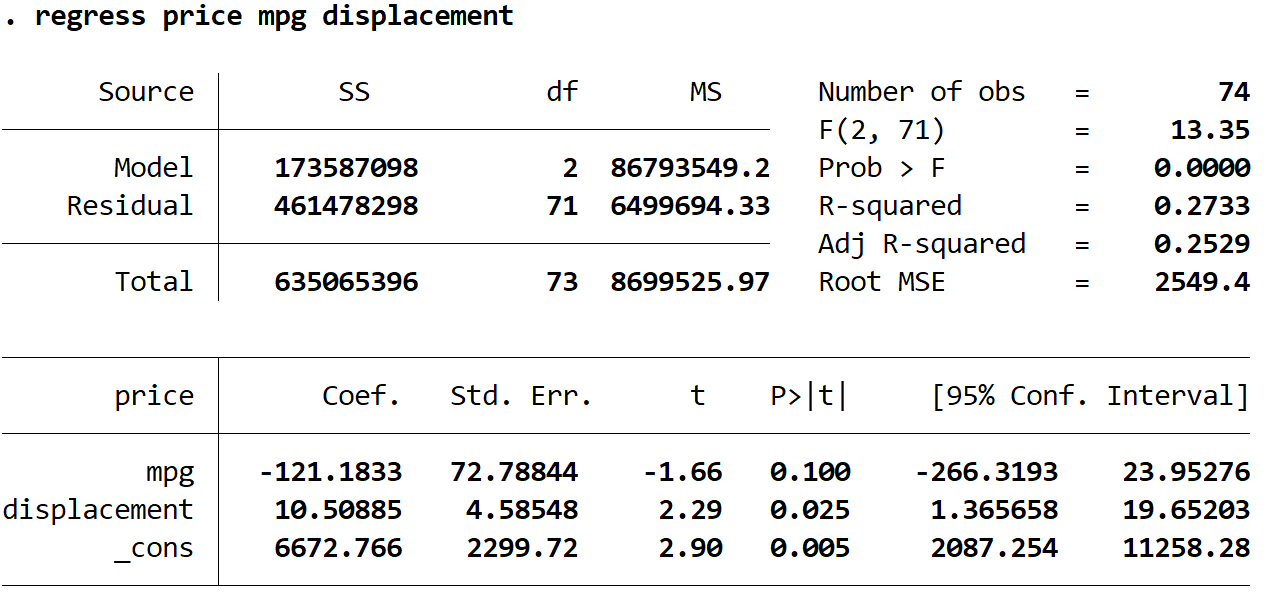
Étape 3 : Calculez les résidus .

Rappelons qu’un résidu est simplement la différence entre la valeur de réponse prévue (telle que calculée par l’équation de régression estimée) et la valeur de réponse réelle.

Nous pouvons obtenir les résidus de chaque prédiction en utilisant la commande résidus et en stockant ces valeurs dans une variable nommée comme nous le souhaitons. Dans ce cas, nous utiliserons le nom resid_price :

prédire resid_price, résidus

Étape 4 : Créez le tracé QQ.

Maintenant que nous avons une liste de résidus, nous pouvons créer un tracé QQ à l’aide de la commande qnorm :

qnorm prix_résid

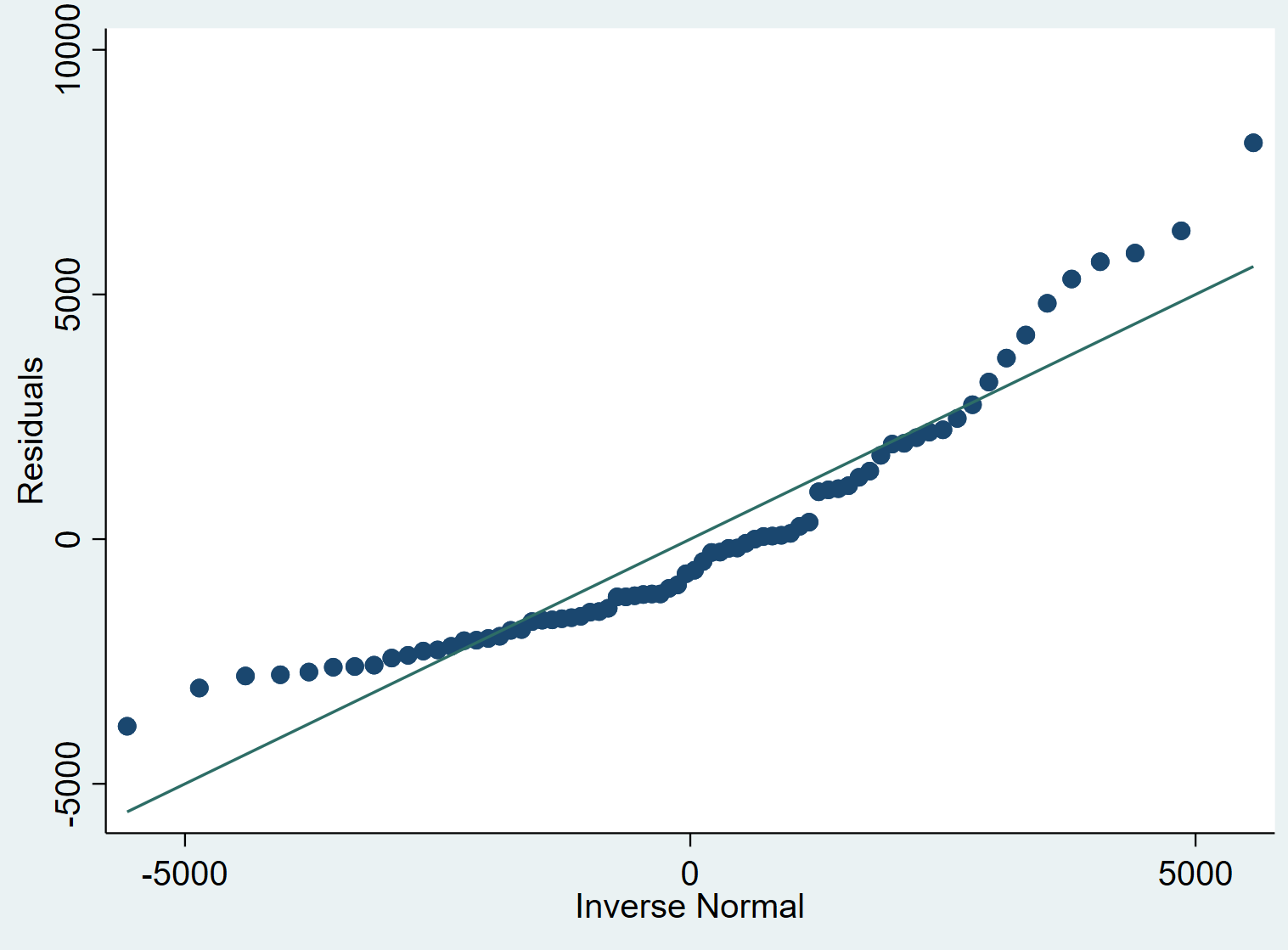
Étape 5 : Interprétez le tracé QQ.

L’idée derrière un tracé QQ est simple : si les résidus suivent une ligne à peu près droite à un angle de 45 degrés, alors les résidus sont à peu près normalement distribués. Nous pouvons voir dans notre graphique QQ ci-dessus que les résidus ont tendance à s’écarter un peu de la ligne de 45 degrés, en particulier aux extrémités, ce qui pourrait indiquer qu’ils ne sont pas normalement distribués.

Bien qu’un tracé QQ ne soit pas un test statistique formel, il offre un moyen simple de vérifier visuellement si les résidus sont normalement distribués ou non.

S’il s’avère que vos résidus s’écartent considérablement de la ligne de 45 degrés dans le graphique QQ, vous pouvez envisager d’effectuer une transformation sur la variable de réponse dans votre régression, par exemple en utilisant la racine carrée ou le log de la variable de réponse.

Si les résidus ne s’écartent que légèrement, vous n’avez pas à vous soucier de la transformation de la variable de réponse, car la régression est assez robuste aux écarts par rapport à la normalité.