Quand utiliser Ridge & Régression au lasso

Dans la régression linéaire multiple ordinaire, nous utilisons un ensemble de p variables prédictives et une variable de réponse pour ajuster un modèle de la forme :

Y = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p + ε

Les valeurs de β ₀ , β ₁ , B ₂ , … , β _p sont choisies en utilisant la méthode des moindres carrés, qui minimise la somme des carrés des résidus (RSS) :

RSS = Σ(y _je – ŷ _je ) ²

où:

• Σ : Un symbole qui signifie « somme »
• y _i : la valeur de réponse réelle pour la ^ième observation
• ŷ _i : La valeur de réponse prédite pour la i ^ème observation

Le problème de la multicolinéarité en régression

Un problème qui survient souvent dans la pratique avec la régression linéaire multiple est la multicolinéarité – lorsque deux ou plusieurs variables prédictives sont fortement corrélées les unes aux autres, de sorte qu’elles ne fournissent pas d’informations uniques ou indépendantes dans le modèle de régression.

Cela peut rendre les estimations des coefficients du modèle peu fiables et présenter une variance élevée. Autrement dit, lorsque le modèle est appliqué à un nouvel ensemble de données qu’il n’a jamais vu auparavant, il est susceptible de fonctionner de manière médiocre.

Éviter la multicolinéarité : régression Ridge & Lasso

Deux méthodes que nous pouvons utiliser pour contourner ce problème de multicolinéarité sont la régression par crête et la régression par lasso .

La régression Ridge cherche à minimiser les éléments suivants :

• RSS + λΣβ _j ²

La régression Lasso cherche à minimiser les éléments suivants :

• RSS + λΣ|β _j |

Dans les deux équations, le deuxième terme est appelé pénalité de retrait .

Lorsque λ = 0, ce terme de pénalité n’a aucun effet et la régression par crête et la régression par lasso produisent les mêmes estimations de coefficient que les moindres carrés.

Cependant, à mesure que λ s’approche de l’infini, la pénalité de retrait devient plus influente et les variables prédictives qui ne sont pas importables dans le modèle diminuent vers zéro.

Avec la régression Lasso, il est possible que certains coefficients deviennent complètement nuls lorsque λ devient suffisamment grand.

Avantages et inconvénients de la régression Ridge & Lasso

L’ avantage de la régression Ridge et Lasso par rapport à la régression des moindres carrés réside dans le compromis biais-variance .

Rappelons que l’erreur quadratique moyenne (MSE) est une métrique que nous pouvons utiliser pour mesurer la précision d’un modèle donné et elle est calculée comme suit :

MSE = Var( f̂( x ₀ )) + [Biais( f̂( x ₀ ))] ² + Var(ε)

MSE = Variance + Biais ² + Erreur irréductible

L’idée de base de la régression Ridge et de la régression Lasso est d’introduire un petit biais afin que la variance puisse être considérablement réduite, ce qui conduit à une MSE globale plus faible.

Pour illustrer cela, considérons le graphique suivant :

Notez que lorsque λ augmente, la variance diminue considérablement avec une très faible augmentation du biais. Cependant, au-delà d’un certain point, la variance diminue moins rapidement et la diminution des coefficients entraîne une sous-estimation significative de ceux-ci, ce qui entraîne une forte augmentation du biais.

Nous pouvons voir sur le graphique que le MSE du test est le plus bas lorsque nous choisissons une valeur pour λ qui produit un compromis optimal entre biais et variance.

Lorsque λ = 0, le terme de pénalité dans la régression au lasso n’a aucun effet et produit donc les mêmes estimations de coefficient que les moindres carrés. Cependant, en augmentant λ jusqu’à un certain point, nous pouvons réduire le MSE global du test.

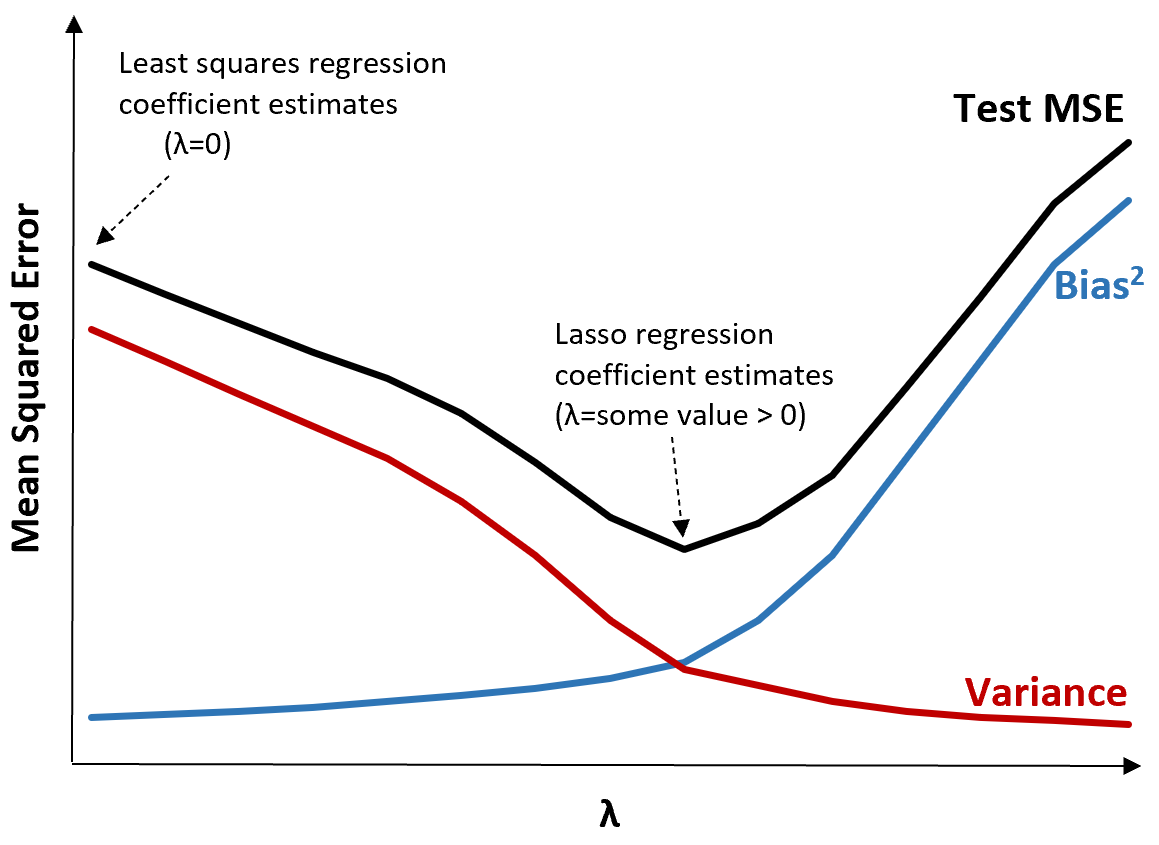
Cela signifie que l’ajustement du modèle par régression de crête et de lasso peut potentiellement produire des erreurs de test plus petites que l’ajustement du modèle par régression des moindres carrés.

L’ inconvénient de la régression Ridge et Lasso est qu’il devient difficile d’interpréter les coefficients dans le modèle final car ils se rétrécissent vers zéro.

Ainsi, la régression Ridge et Lasso doit être utilisée lorsque vous souhaitez optimiser la capacité prédictive plutôt que l’inférence.

Régression Ridge vs Lasso : quand utiliser chacun

La régression l asso et la régression ridge sont connues sous le nom de méthodes de régularisation car elles tentent toutes deux de minimiser la somme des carrés résiduels (RSS) ainsi qu’un certain terme de pénalité.

En d’autres termes, ils contraignent ou régularisent les estimations des coefficients du modèle.

Cela soulève naturellement la question : la régression par crête ou par lasso est-elle meilleure ?

Dans les cas où seul un petit nombre de variables prédictives sont significatives, la régression par lasso a tendance à mieux fonctionner car elle est capable de réduire complètement les variables insignifiantes à zéro et de les supprimer du modèle.

Cependant, lorsque de nombreuses variables prédictives sont significatives dans le modèle et que leurs coefficients sont à peu près égaux, la régression de crête a tendance à mieux fonctionner car elle conserve tous les prédicteurs dans le modèle.

Pour déterminer quel modèle est le meilleur pour faire des prédictions, nous effectuons généralement une validation croisée k fois et choisissons le modèle qui produit l’erreur quadratique moyenne de test la plus faible.

Ressources additionnelles

Les didacticiels suivants fournissent une introduction à la régression Ridge et à la régression Lasso :

• Introduction à la régression Ridge
• Introduction à la régression au lasso

Les didacticiels suivants expliquent comment effectuer les deux types de régression en R et Python :

• Régression de crête dans R
• Régression Ridge en Python
• Régression Lasso dans R
• Régression Lasso en Python