Ce qui est considéré comme un « faible » ; Corrélation?
En statistiques, nous cherchons souvent à comprendre comment deux variables sont liées l’une à l’autre. Par exemple, nous pourrions vouloir savoir :
- Quelle est la relation entre le nombre d’heures d’études d’un étudiant et la note qu’il obtient à l’examen ?
- Quelle est la relation entre la température extérieure et le nombre de barres glacées vendues par un food truck ?
- Quelle est la relation entre les dollars dépensés en publicité et le revenu total gagné pour une entreprise donnée ?
Dans chaque scénario, nous souhaitons comprendre la relation entre deux variables.
L’un des moyens les plus courants de quantifier une relation entre deux variables consiste à utiliser le coefficient de corrélation de Pearson , qui est une mesure de l’association linéaire entre deux variables.
Il prend toujours une valeur comprise entre -1 et 1 où :
- -1 indique une corrélation linéaire parfaitement négative entre deux variables
- 0 indique aucune corrélation linéaire entre deux variables
- 1 indique une corrélation linéaire parfaitement positive entre deux variables
Souvent noté r , ce nombre nous aide à comprendre la force de la relation entre deux variables. Plus r est proche de zéro, plus la relation entre les deux variables est faible .
Il est important de noter que deux variables peuvent avoir une faible corrélation positive ou une faible corrélation négative .
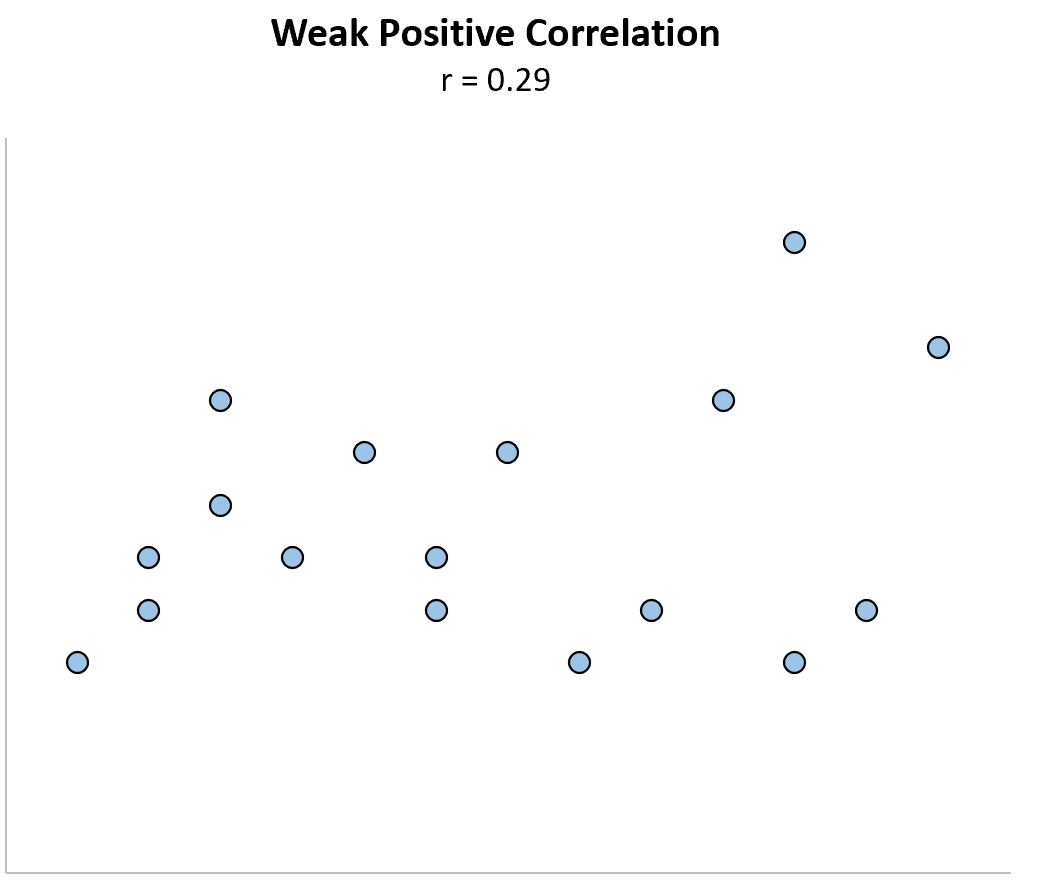
Faible corrélation positive : lorsqu’une variable augmente, l’autre variable a tendance à augmenter également, mais de manière faible ou peu fiable.
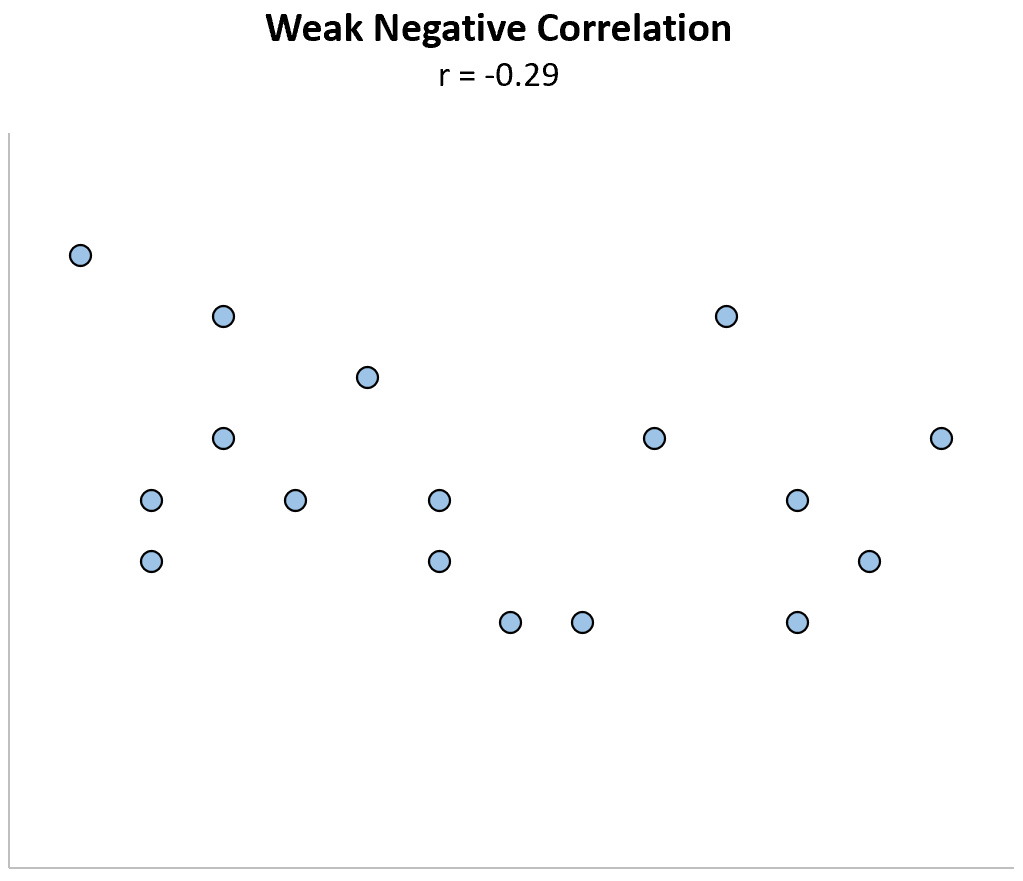
Faible corrélation négative : lorsqu’une variable augmente, l’autre variable a tendance à diminuer, mais de manière faible ou peu fiable.
Le tableau suivant montre la règle empirique pour interpréter la force de la relation entre deux variables en fonction de la valeur de r :
| Valeur absolue de r | Force de la relation |
|---|---|
| r < 0,25 | Pas de relation |
| 0,25 < r < 0,5 | Faible relation |
| 0,5 < r < 0,75 | Relation modérée |
| r > 0,75 | Relation forte |
La corrélation entre deux variables est considérée comme faible si la valeur absolue de r est comprise entre 0,25 et 0,5.
Cependant, la définition d’une corrélation « faible » peut varier d’un domaine à l’autre.
Médical
Dans les domaines médicaux, la définition d’une relation « faible » est souvent bien inférieure. Si la relation entre la prise d’un certain médicament et la réduction des crises cardiaques est r = 0,2, cela pourrait être considéré comme « aucune relation » dans d’autres domaines, mais en médecine, c’est suffisamment important pour qu’il vaille la peine de prendre le médicament pour réduire les risques de crises cardiaques. avoir une crise cardiaque.
Ressources humaines
Dans un domaine comme les ressources humaines, des corrélations plus faibles sont également utilisées plus souvent. Par exemple, il a été démontré que la corrélation entre la moyenne cumulative des études universitaires et le rendement au travail est d’environ r = 0,16 . C’est assez faible, mais il est suffisamment important pour qu’une entreprise puisse au moins l’examiner lors d’un processus d’entretien.
Technologie
Dans les domaines technologiques, la corrélation entre les variables pourrait devoir être beaucoup plus élevée pour être considérée comme « faible ». Par exemple, si une entreprise crée une voiture autonome et que la corrélation entre les décisions de virage de la voiture et la probabilité d’éviter un accident est r = 0,95 , cela peut être considéré comme une corrélation « faible » et est probablement trop faible pour que la voiture puisse être considéré comme sûr, car une mauvaise décision peut être fatale.
Utiliser des nuages de points pour visualiser les corrélations
Lorsque vous calculez le coefficient de corrélation entre deux variables, il est utile de créer un nuage de points pour visualiser également la corrélation.
En particulier, les nuages de points offrent deux avantages :
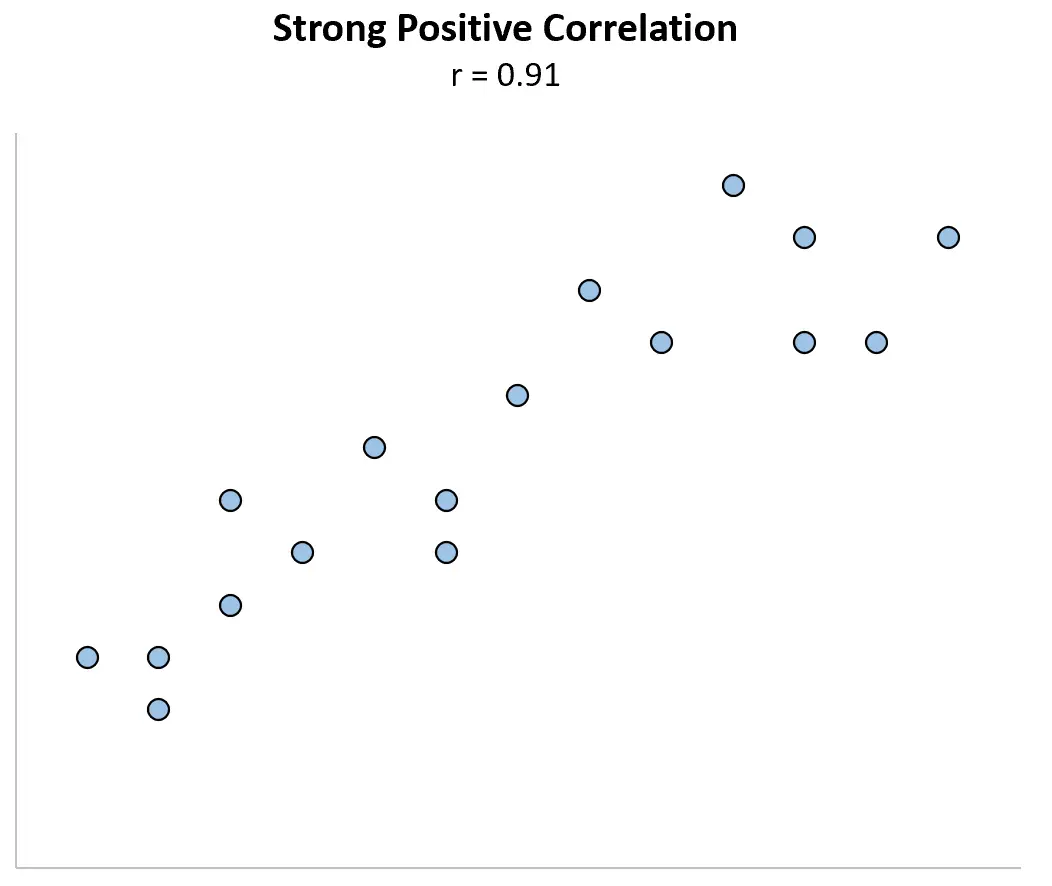
1. Les nuages de points peuvent vous aider à identifier les valeurs aberrantes qui affectent le coefficient de corrélation.
Une valeur aberrante extrême peut avoir un impact important sur le coefficient de corrélation. Prenons l’exemple ci-dessous, dans lequel les variables X et Y ont un coefficient de corrélation de Pearson de r = 0,91 .
Imaginez maintenant que nous modifiions le premier point de données pour qu’il soit beaucoup plus grand. Le coefficient de corrélation devient soudainement r = 0,29 .
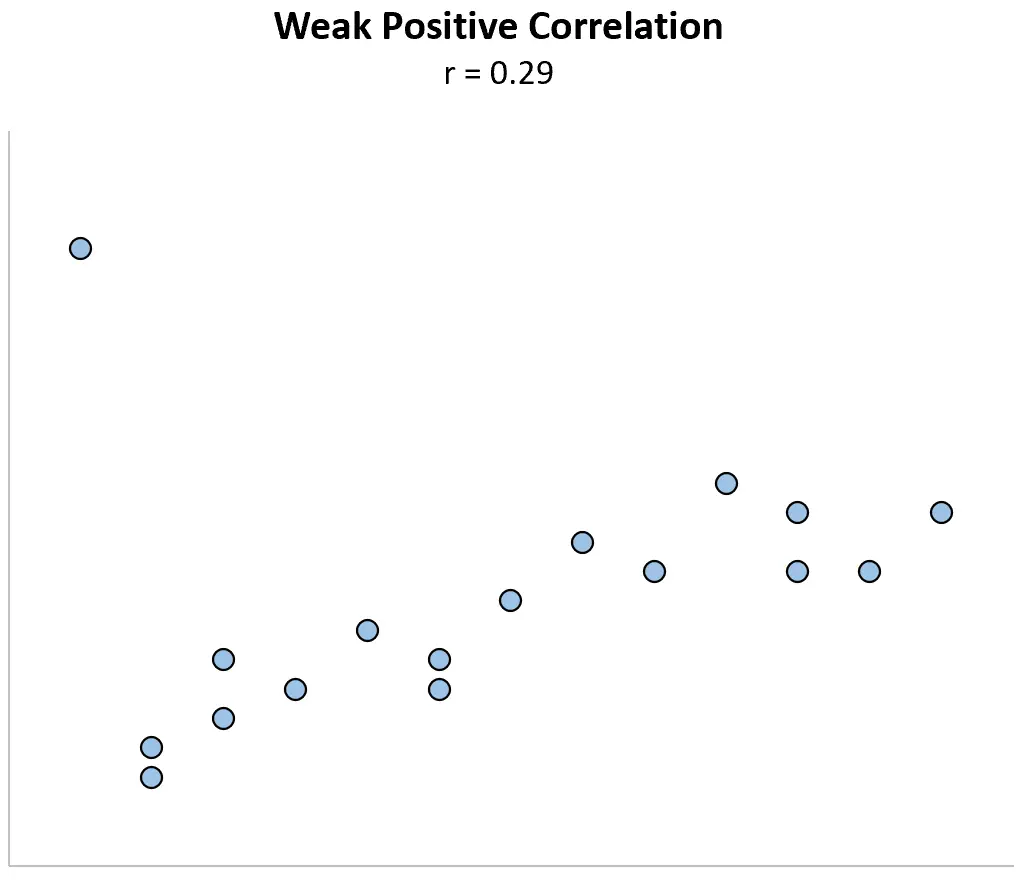
Ce point de données unique fait passer le coefficient de corrélation d’une relation fortement positive à une relation faiblement positive.
(2) Les nuages de points peuvent vous aider à identifier les relations non linéaires entre les variables.
Un coefficient de corrélation de Pearson nous indique simplement si deux variables sont linéairement liées. Mais même si un coefficient de corrélation de Pearson nous indique que deux variables ne sont pas corrélées, elles pourraient quand même entretenir une sorte de relation non linéaire.
Par exemple, considérons le nuage de points ci-dessous entre les variables X et Y , dans lequel leur corrélation est r = 0,00 .
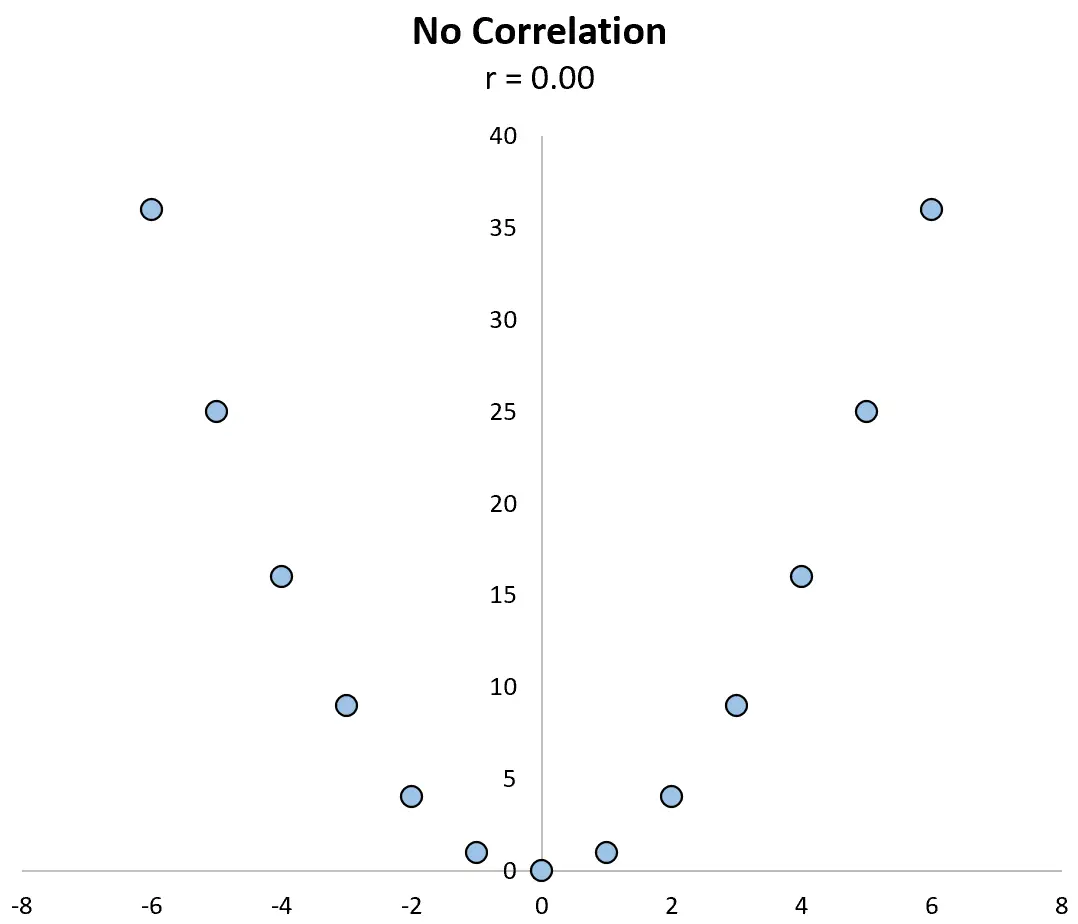
Les variables n’ont clairement pas de relation linéaire, mais elles ont une relation non linéaire : les valeurs y sont simplement les valeurs x au carré.
Un coefficient de corrélation à lui seul ne pourrait pas détecter cette relation, mais un nuage de points le pourrait.
Conclusion
En résumé:
1. En règle générale, un coefficient de corrélation compris entre 0,25 et 0,5 est considéré comme une corrélation « faible » entre deux variables.
2. Cette règle empirique peut varier d’un domaine à l’autre. Par exemple, une corrélation beaucoup plus faible pourrait être considérée comme faible dans un domaine médical par rapport à un domaine technologique. Assurez-vous de faire appel à votre expertise en la matière pour décider ce qui est considéré comme une faible corrélation.
3. Lorsque vous utilisez un coefficient de corrélation pour décrire la relation entre deux variables, il est également utile de créer un nuage de points afin que vous puissiez identifier les valeurs aberrantes dans l’ensemble de données ainsi qu’une relation non linéaire potentielle.
Ressources additionnelles
Qu’est-ce qui est considéré comme une corrélation « forte » ?
Calculateur de matrice de corrélation
Corrélation vs association : quelle est la différence ?
