Randomisation en statistiques : définition & Exemple

Dans le domaine des statistiques, la randomisation fait référence à l’acte d’assigner au hasard les sujets d’une étude à différents groupes de traitement.

Par exemple, supposons que des chercheurs recrutent 100 sujets pour participer à une étude dans laquelle ils espèrent comprendre si deux pilules différentes ont ou non des effets différents sur la tension artérielle.

Ils peuvent décider d’utiliser un générateur de nombres aléatoires pour attribuer au hasard à chaque sujet l’utilisation de la pilule n°1 ou de la pilule n°2.

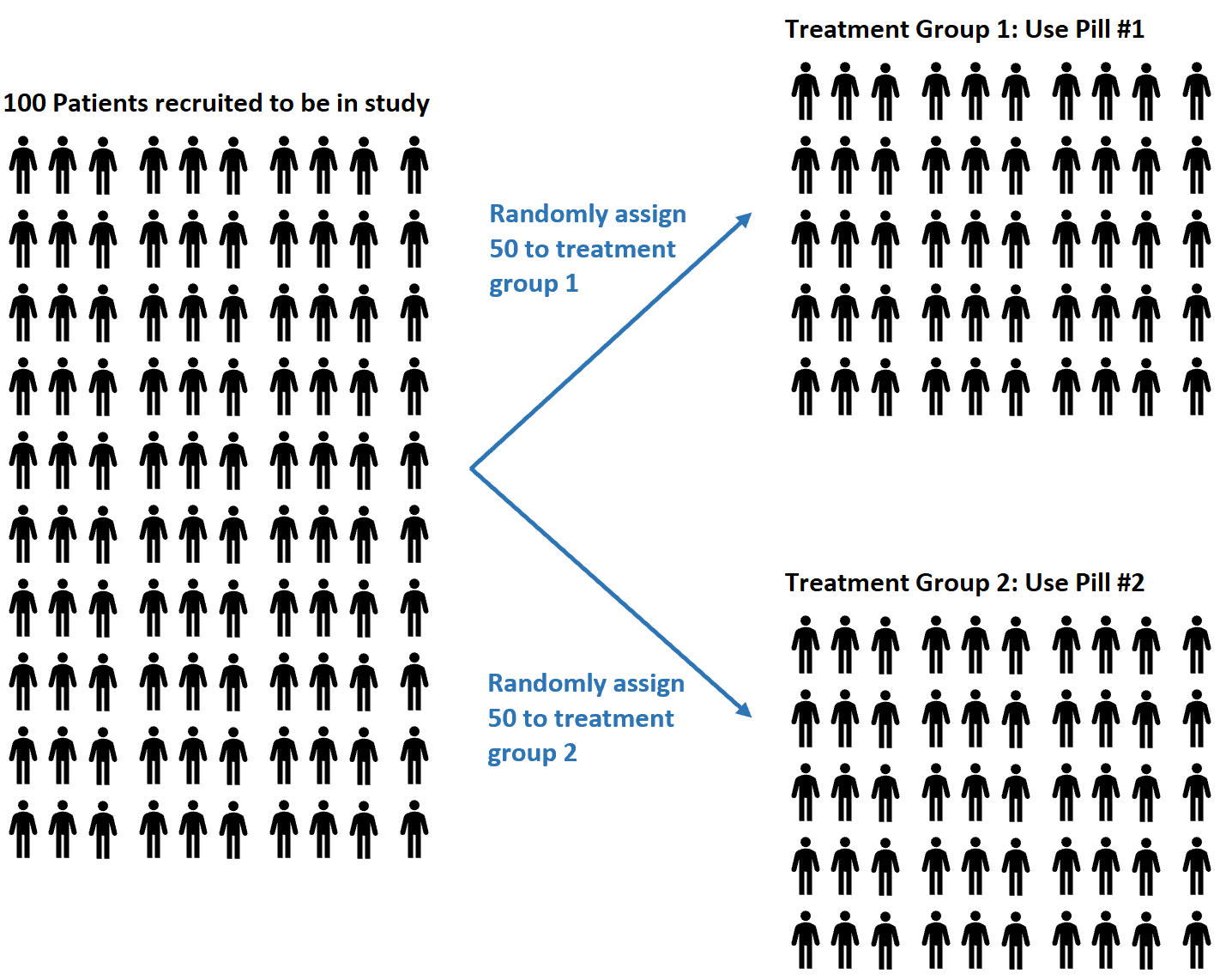
Avantages de la randomisation

Le but de la randomisation est de contrôler les variables cachées – des variables qui ne sont pas directement incluses dans une analyse, mais qui ont pourtant un impact sur l’analyse d’une manière ou d’une autre.

Par exemple, si les chercheurs étudient les effets de deux pilules différentes sur la tension artérielle, les variables cachées suivantes pourraient affecter l’analyse :

• Habitudes tabagiques
• Régime
• Exercice

En assignant au hasard les sujets aux groupes de traitement, nous maximisons les chances que les variables cachées affectent également les deux groupes de traitement.

Cela signifie que toute différence de tension artérielle peut être attribuée au type de pilule plutôt qu’à l’effet d’une variable cachée.

Bloquer la randomisation

Une extension de la randomisation est connue sous le nom de randomisation par blocs . Il s’agit du processus consistant d’abord à séparer les sujets en blocs, puis à utiliser la randomisation pour attribuer les sujets au sein des blocs à différents traitements.

Par exemple, si les chercheurs veulent savoir si deux pilules différentes affectent différemment la tension artérielle, ils peuvent d’abord séparer tous les sujets en deux blocs en fonction du sexe : homme ou femme.

Ensuite, dans chaque bloc, ils peuvent utiliser la randomisation pour assigner au hasard les sujets à utiliser soit la pilule n°1, soit la pilule n°2.

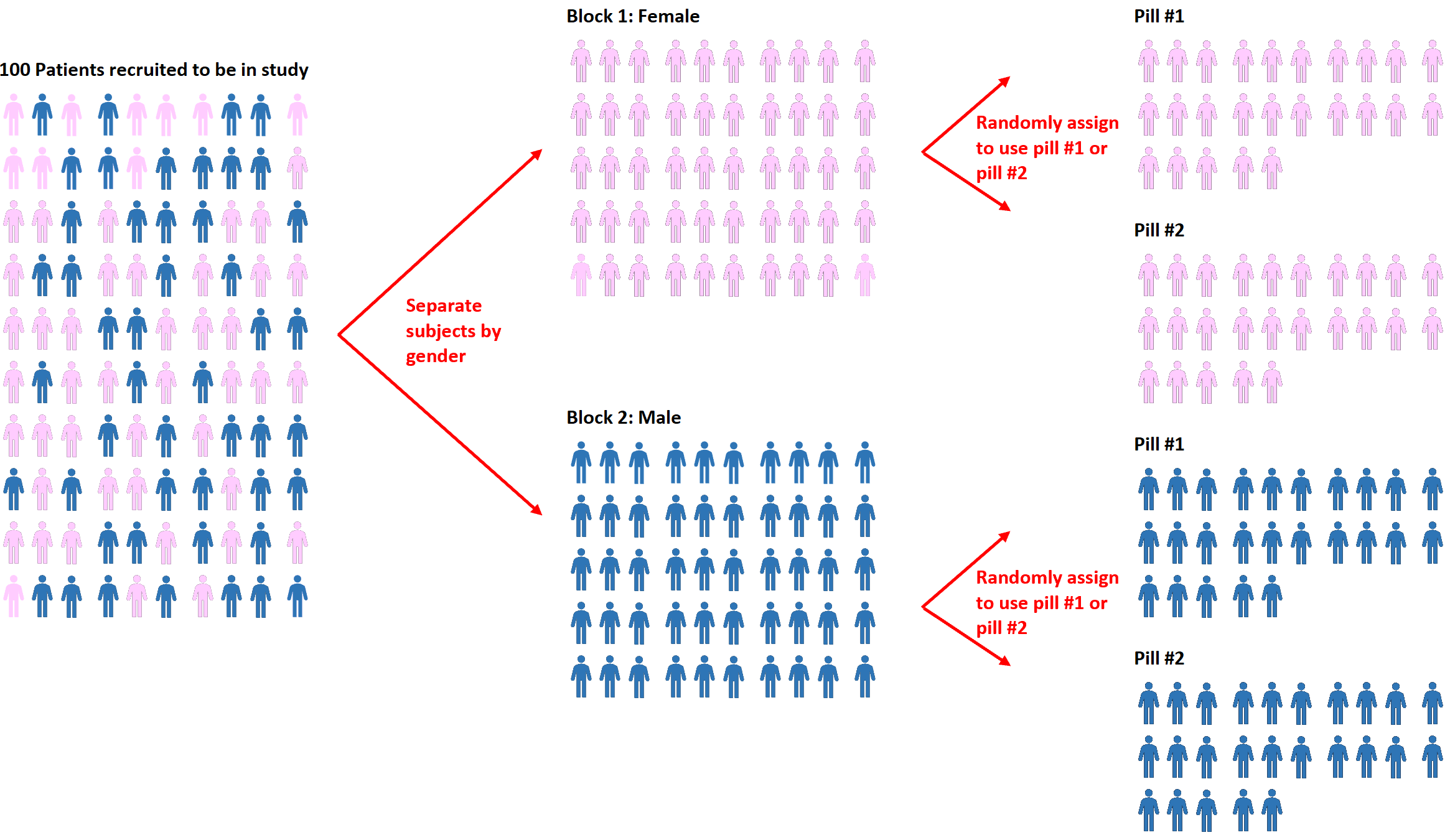
L’avantage de cette approche est que les chercheurs peuvent contrôler directement tout effet que le sexe peut avoir sur la tension artérielle, puisque nous savons que les hommes et les femmes sont susceptibles de réagir différemment à chaque pilule.

En utilisant le sexe comme bloc, nous sommes en mesure d’éliminer cette variable comme source potentielle de variation. S’il existe des différences de tension artérielle entre les deux pilules, nous pouvons alors savoir que le sexe n’est pas la cause sous-jacente de ces différences.

Ressources additionnelles

Blocage dans les statistiques : définition et exemple
Randomisation de blocs permutés : définition et exemple
Variables cachées : définition et exemples