Introduction à la régression Ridge

Dans la régression linéaire multiple ordinaire, nous utilisons un ensemble de p variables prédictives et une variable de réponse pour ajuster un modèle de la forme :

Y = β ₀ + β ₁ X ₁ + β ₂ X ₂ + … + β _p X _p + ε

où:

• Y : La variable de réponse
• X _j : la j ^ème variable prédictive
• β _j : L’effet moyen sur Y d’une augmentation d’une unité de X _j , en maintenant fixes tous les autres prédicteurs
• ε : Le terme d’erreur

Les valeurs de β ₀ , β ₁ , B ₂ , … , β _p sont choisies en utilisant la méthode des moindres carrés , qui minimise la somme des carrés des résidus (RSS) :

RSS = Σ(y _je – ŷ _je ) ²

où:

• Σ : Un symbole grec qui signifie somme
• y _i : la valeur de réponse réelle pour la ^ième observation
• ŷ _i : La valeur de réponse prédite basée sur le modèle de régression linéaire multiple

Cependant, lorsque les variables prédictives sont fortement corrélées, la multicolinéarité peut devenir un problème. Cela peut rendre les estimations des coefficients du modèle peu fiables et présenter une variance élevée.

Une façon de contourner ce problème sans supprimer complètement certaines variables prédictives du modèle consiste à utiliser une méthode connue sous le nom de régression de crête , qui cherche plutôt à minimiser les éléments suivants :

RSS + λΣβ _j ²

où j va de 1 à p et λ ≥ 0.

Ce deuxième terme de l’équation est connu sous le nom de pénalité de retrait .

Lorsque λ = 0, ce terme de pénalité n’a aucun effet et la régression de crête produit les mêmes estimations de coefficient que les moindres carrés. Cependant, à mesure que λ se rapproche de l’infini, la pénalité de retrait devient plus influente et les estimations du coefficient de régression de crête se rapprochent de zéro.

En général, les variables prédictives les moins influentes dans le modèle diminueront le plus rapidement vers zéro.

Pourquoi utiliser la régression Ridge ?

L’avantage de la régression Ridge par rapport à la régression des moindres carrés réside dans le compromis biais-variance .

Rappelons que l’erreur quadratique moyenne (MSE) est une métrique que nous pouvons utiliser pour mesurer la précision d’un modèle donné et elle est calculée comme suit :

MSE = Var( f̂( x ₀ )) + [Biais( f̂( x ₀ ))] ² + Var(ε)

MSE = Variance + Biais ² + Erreur irréductible

L’idée de base de la régression Ridge est d’introduire un petit biais afin que la variance puisse être considérablement réduite, ce qui conduit à une MSE globale plus faible.

Pour illustrer cela, considérons le graphique suivant :

Notez que lorsque λ augmente, la variance diminue considérablement avec une très faible augmentation du biais. Cependant, au-delà d’un certain point, la variance diminue moins rapidement et la diminution des coefficients entraîne une sous-estimation significative de ceux-ci, ce qui entraîne une forte augmentation du biais.

Nous pouvons voir sur le graphique que le MSE du test est le plus bas lorsque nous choisissons une valeur pour λ qui produit un compromis optimal entre biais et variance.

Lorsque λ = 0, le terme de pénalité dans la régression de crête n’a aucun effet et produit donc les mêmes estimations de coefficient que les moindres carrés. Cependant, en augmentant λ jusqu’à un certain point, nous pouvons réduire le MSE global du test.

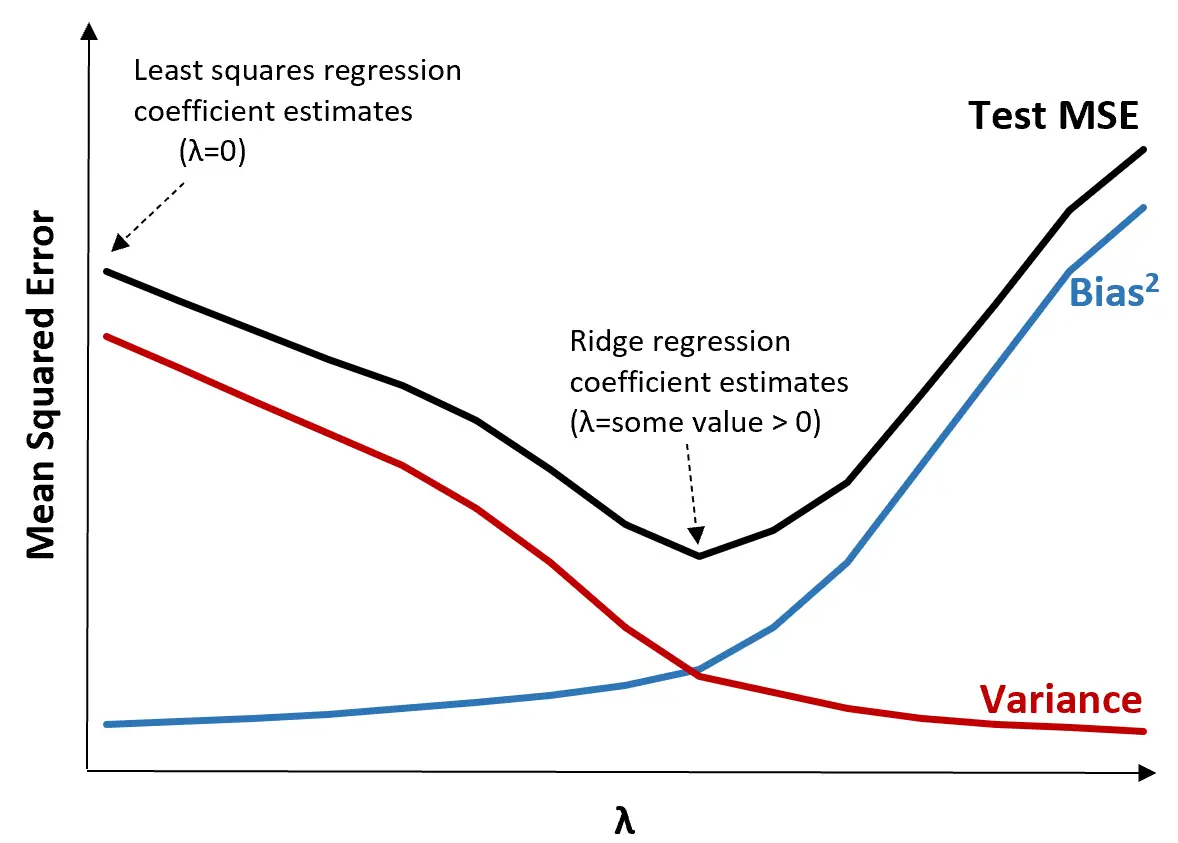
Cela signifie que l’ajustement du modèle par régression de crête produira des erreurs de test plus petites que l’ajustement du modèle par régression des moindres carrés.

Étapes pour effectuer une régression de crête en pratique

Les étapes suivantes peuvent être utilisées pour effectuer une régression de crête :

Étape 1 : Calculez la matrice de corrélation et les valeurs VIF pour les variables prédictives.

Tout d’abord, nous devons produire une matrice de corrélation et calculer les valeurs VIF (variance inflation factor) pour chaque variable prédictive.

Si nous détectons une forte corrélation entre les variables prédictives et les valeurs VIF élevées (certains textes définissent une valeur VIF « élevée » comme 5 tandis que d’autres utilisent 10), alors la régression de crête est probablement appropriée.

Cependant, s’il n’y a pas de multicolinéarité dans les données, il n’est peut-être pas nécessaire d’effectuer une régression de crête en premier lieu. Au lieu de cela, nous pouvons effectuer une régression des moindres carrés ordinaires.

Étape 2 : Standardisez chaque variable prédictive.

Avant d’effectuer une régression de crête, nous devons mettre à l’échelle les données de telle sorte que chaque variable prédictive ait une moyenne de 0 et un écart type de 1. Cela garantit qu’aucune variable prédictive unique n’a une influence excessive lors de l’exécution d’une régression de crête.

Étape 3 : Ajustez le modèle de régression de crête et choisissez une valeur pour λ.

Il n’existe pas de formule exacte que nous pouvons utiliser pour déterminer quelle valeur utiliser pour λ. En pratique, il existe deux manières courantes de choisir λ :

(1) Créez un tracé de trace Ridge. Il s’agit d’un graphique qui visualise les valeurs des estimations de coefficient lorsque λ augmente vers l’infini. En règle générale, nous choisissons λ comme valeur à laquelle la plupart des estimations de coefficients commencent à se stabiliser.

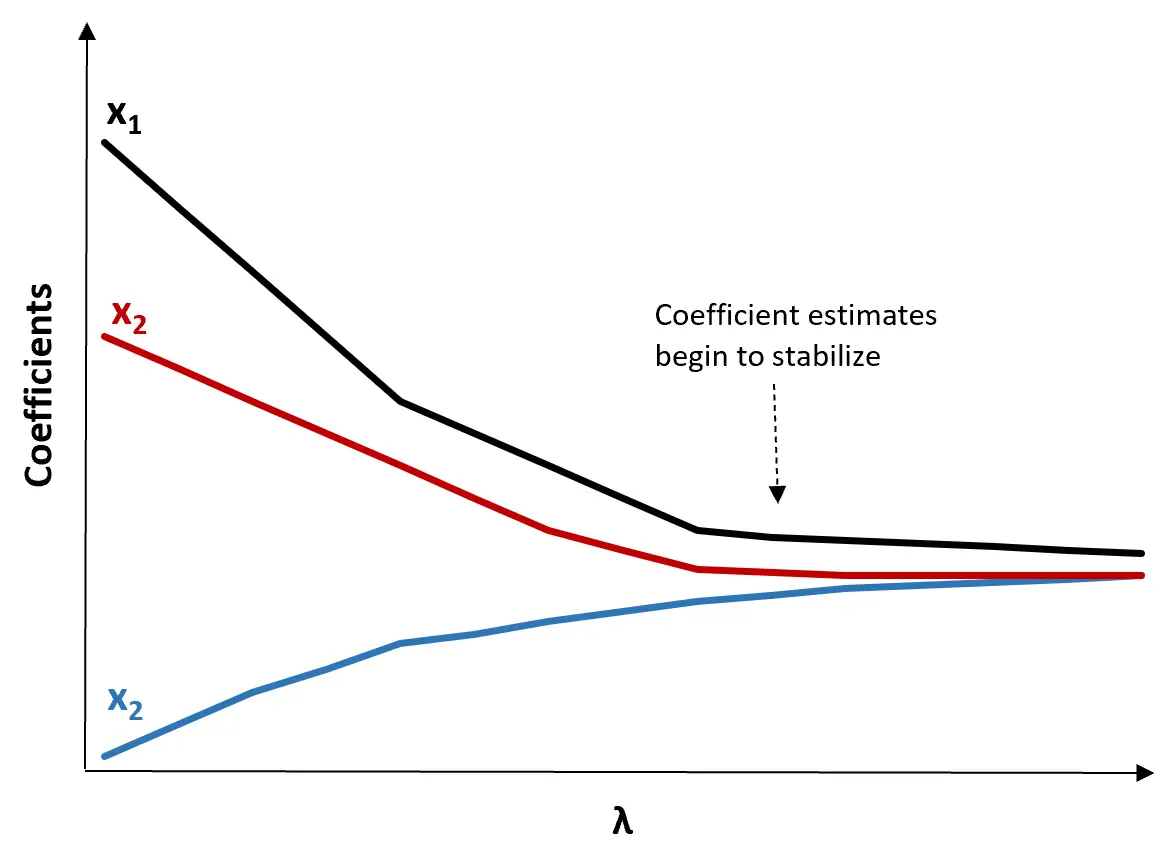
(2) Calculez le test MSE pour chaque valeur de λ.

Une autre façon de choisir λ consiste simplement à calculer le MSE de test de chaque modèle avec différentes valeurs de λ et à choisir λ comme étant la valeur qui produit le MSE de test le plus bas.

Avantages et inconvénients de la régression Ridge

Le plus grand avantage de la régression Ridge est sa capacité à produire une erreur quadratique moyenne (MSE) de test inférieure à celle des moindres carrés lorsque la multicolinéarité est présente.

Cependant, le plus gros inconvénient de la régression Ridge est son incapacité à effectuer une sélection de variables puisqu’elle inclut toutes les variables prédictives dans le modèle final. Étant donné que certains prédicteurs seront réduits très près de zéro, cela peut rendre difficile l’interprétation des résultats du modèle.

En pratique, la régression Ridge a le potentiel de produire un modèle capable de faire de meilleures prédictions par rapport à un modèle des moindres carrés, mais il est souvent plus difficile d’interpréter les résultats du modèle.

Selon que l’interprétation du modèle ou la précision des prévisions est plus importante pour vous, vous pouvez choisir d’utiliser les moindres carrés ordinaires ou la régression par crête dans différents scénarios.

Régression Ridge en R & Python

Les didacticiels suivants expliquent comment effectuer une régression de crête dans R et Python, les deux langages les plus couramment utilisés pour ajuster les modèles de régression de crête :

Régression de crête dans R (étape par étape)
Régression Ridge en Python (étape par étape)