Introduction à la régression linéaire simple

La régression linéaire simple est une méthode statistique que vous pouvez utiliser pour comprendre la relation entre deux variables, x et y.

Une variable, x , est connue sous le nom de variable prédictive .

L’autre variable, y , est connue sous le nom de variable de réponse .

Par exemple, supposons que nous disposions de l’ensemble de données suivant avec le poids et la taille de sept individus :

Laissez le poids être la variable prédictive et laissez la taille être la variable de réponse.

Si nous représentons graphiquement ces deux variables à l’aide d’un nuage de points , avec le poids sur l’axe des x et la hauteur sur l’axe des y, voici à quoi cela ressemblerait :

Supposons que nous souhaitions comprendre la relation entre le poids et la taille. À partir du nuage de points, nous pouvons clairement voir qu’à mesure que le poids augmente, la taille a également tendance à augmenter, mais pour quantifier réellement cette relation entre le poids et la taille, nous devons utiliser la régression linéaire.

En utilisant la régression linéaire, nous pouvons trouver la ligne qui « correspond » le mieux à nos données. Cette droite est connue sous le nom de droite de régression des moindres carrés et peut être utilisée pour nous aider à comprendre les relations entre le poids et la taille.

Habituellement, vous utiliserez un logiciel comme Microsoft Excel, SPSS ou une calculatrice graphique pour trouver l’équation de cette ligne.

La formule de la droite de meilleur ajustement s’écrit :

ŷ = b ₀ + b ₁ x

où ŷ est la valeur prédite de la variable de réponse, b ₀ est l’ordonnée à l’origine, b ₁ est le coefficient de régression et x est la valeur de la variable prédictive.

Connexe : 4 exemples d’utilisation de la régression linéaire dans la vie réelle

Trouver la « ligne la mieux adaptée »

Pour cet exemple, nous pouvons simplement brancher nos données dans le calculateur de régression linéaire statistique et appuyer sur Calculer :

Le calculateur trouve automatiquement la droite de régression des moindres carrés :

ŷ = 32,7830 + 0,2001x

Si nous effectuons un zoom arrière sur notre nuage de points précédent et ajoutons cette ligne au graphique, voici à quoi cela ressemblerait :

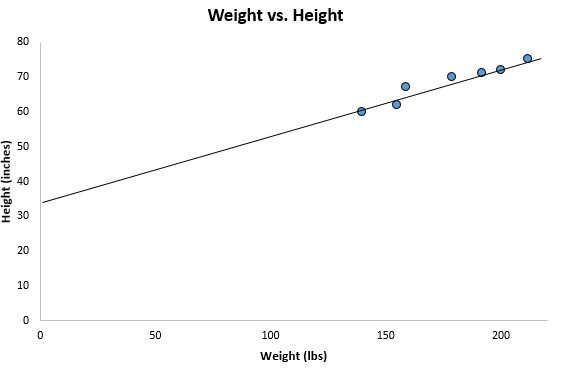
Remarquez comment nos points de données sont étroitement dispersés autour de cette ligne. En effet, cette droite de régression des moindres carrés est la droite la mieux adaptée à nos données parmi toutes les droites possibles que nous pourrions tracer.

Comment interpréter une droite de régression des moindres carrés

Voici comment interpréter cette droite de régression des moindres carrés : ŷ = 32,7830 + 0,2001x

b ₀ = 32,7830 . Cela signifie que lorsque le poids variable prédicteur est de zéro livre, la hauteur prévue est de 32,7830 pouces. Parfois, la valeur de b ₀ peut être utile à connaître, mais dans cet exemple spécifique, cela n’a pas de sens d’interpréter b ₀ puisqu’une personne ne peut pas peser zéro livre.

b ₁ = 0,2001 . Cela signifie qu’une augmentation d’une unité de x est associée à une augmentation de 0,2001 unité de y . Dans ce cas, une augmentation de poids d’une livre est associée à une augmentation de taille de 0,2001 pouce.

Comment utiliser la droite de régression des moindres carrés

En utilisant cette droite de régression des moindres carrés, nous pouvons répondre à des questions telles que :

Pour une personne qui pèse 170 livres, quelle taille devrions-nous attendre d’elle ?

Pour répondre à cette question, nous pouvons simplement insérer 170 dans notre droite de régression pour x et résoudre pour y :

ŷ = 32,7830 + 0,2001(170) = 66,8 pouces

Pour une personne qui pèse 150 livres, quelle taille devrions-nous attendre d’elle ?

Pour répondre à cette question, nous pouvons insérer 150 dans notre droite de régression pour x et résoudre pour y :

ŷ = 32,7830 + 0,2001(150) = 62,798 pouces

Attention : lorsque vous utilisez une équation de régression pour répondre à des questions comme celles-ci, assurez-vous d’utiliser uniquement des valeurs pour la variable prédictive qui se situent dans la plage de la variable prédictive dans l’ensemble de données d’origine que nous avons utilisé pour générer la droite de régression des moindres carrés. Par exemple, les poids de notre ensemble de données variaient entre 140 et 212 livres. Il est donc logique de répondre aux questions sur la taille prévue lorsque le poids est compris entre 140 et 212 livres.

Le coefficient de détermination

Une façon de mesurer dans quelle mesure la droite de régression des moindres carrés « s’ajuste » aux données consiste à utiliser le coefficient de détermination , noté R ² .

Le coefficient de détermination est la proportion de la variance de la variable de réponse qui peut être expliquée par la variable prédictive.

Le coefficient de détermination peut varier de 0 à 1. Une valeur de 0 indique que la variable de réponse ne peut pas du tout être expliquée par la variable prédictive. Une valeur de 1 indique que la variable de réponse peut être parfaitement expliquée sans erreur par la variable prédictive.

Un R ² compris entre 0 et 1 indique dans quelle mesure la variable de réponse peut être expliquée par la variable prédictive. Par exemple, un R ² de 0,2 indique que 20 % de la variance de la variable de réponse peut être expliquée par la variable prédictive ; un R ² de 0,77 indique que 77 % de la variance de la variable de réponse peut être expliquée par la variable prédictive.

Remarquez que dans notre résultat précédent, nous avons obtenu un R ² de 0,9311, ce qui indique que 93,11 % de la variabilité de la taille peut être expliquée par la variable prédictive du poids :

Cela nous indique que le poids est un très bon indicateur de la taille.

Hypothèses de régression linéaire

Pour que les résultats d’un modèle de régression linéaire soient valides et fiables, nous devons vérifier que les quatre hypothèses suivantes sont remplies :

1. Relation linéaire : Il existe une relation linéaire entre la variable indépendante, x, et la variable dépendante, y.

2. Indépendance : Les résidus sont indépendants. En particulier, il n’existe aucune corrélation entre les résidus consécutifs dans les données de séries chronologiques.

3. Homoscédasticité : Les résidus ont une variance constante à chaque niveau de x.

4. Normalité : Les résidus du modèle sont normalement distribués.

Si une ou plusieurs de ces hypothèses ne sont pas respectées, les résultats de notre régression linéaire peuvent alors être peu fiables, voire trompeurs.

Reportez-vous à cet article pour une explication de chaque hypothèse, comment déterminer si l’hypothèse est remplie et que faire si l’hypothèse n’est pas respectée.