Régression logistique vs régression linéaire : les principales différences
Deux des modèles de régression les plus couramment utilisés sont la régression linéaire et la régression logistique .
Les deux types de modèles de régression sont utilisés pour quantifier la relation entre une ou plusieurs variables prédictives et une variable de réponse , mais il existe quelques différences clés entre les deux modèles :
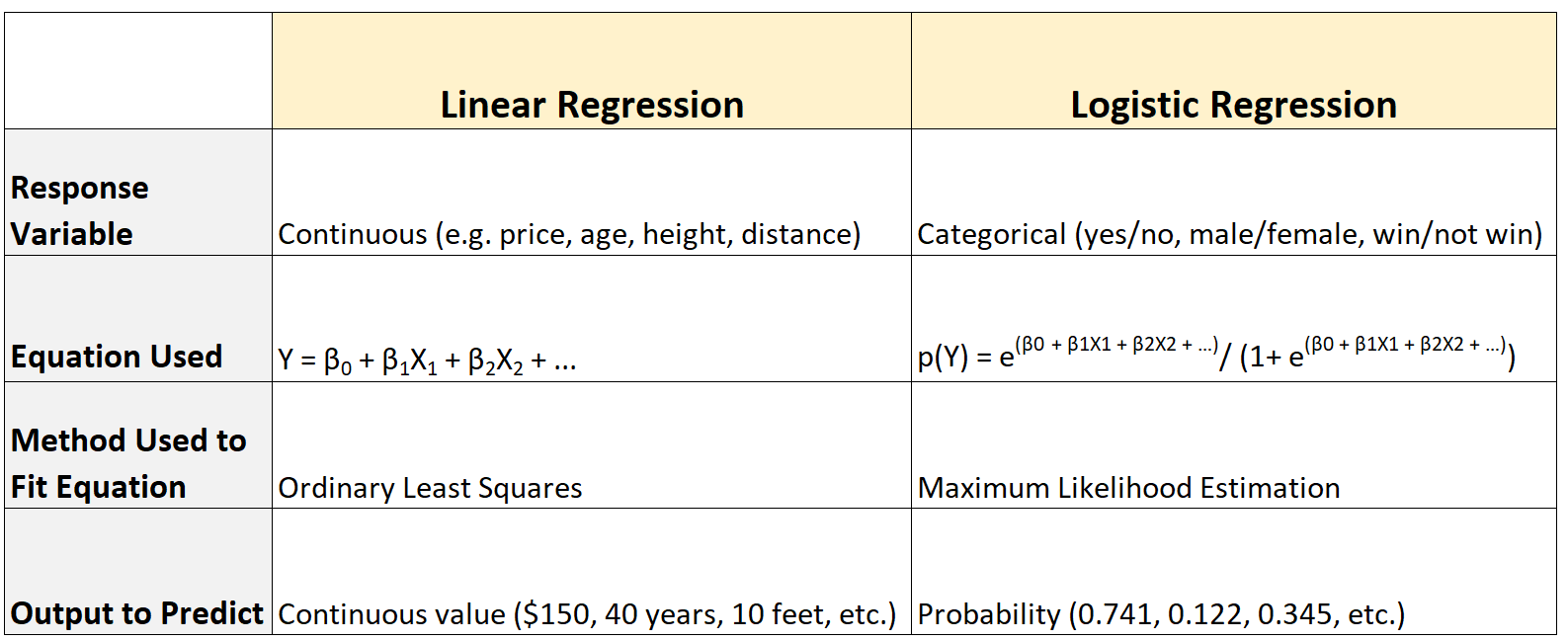
Voici un résumé des différences :
Différence n°1 : type de variable de réponse
Un modèle de régression linéaire est utilisé lorsque la variable de réponse prend une valeur continue telle que :
- Prix
- Hauteur
- Âge
- Distance
A l’inverse, un modèle de régression logistique est utilisé lorsque la variable réponse prend une valeur catégorielle telle que :
- Oui ou non
- Mâle ou femelle
- Gagner ou ne pas gagner
Différence n°2 : équation utilisée
La régression linéaire utilise l’équation suivante pour résumer la relation entre la ou les variables prédictives et la variable de réponse :
Y = β 0 + β 1 X 1 + β 2 X 2 + … + β p X p
où:
- Y : la variable de réponse
- X j : la j ème variable prédictive
- β j : L’effet moyen sur Y d’une augmentation d’une unité de X j , en maintenant fixes tous les autres prédicteurs
A l’inverse, la régression logistique utilise l’équation suivante :
p(X) = e β 0 + β 1 X 1 + β 2 X 2 + … + β p X p / (1 + e β 0 + β 1 X 1 + β 2 X 2 + … + β p X p )
Cette équation est utilisée pour prédire la probabilité qu’une observation individuelle entre dans une certaine catégorie.
Différence n°3 : méthode utilisée pour ajuster l’équation
La régression linéaire utilise une méthode connue sous le nom de moindres carrés ordinaires pour trouver l’équation de régression la mieux adaptée.
À l’inverse, la régression logistique utilise une méthode connue sous le nom d’estimation du maximum de vraisemblance pour trouver l’équation de régression la mieux adaptée.
Différence n°4 : sortie à prédire
La régression linéaire prédit une valeur continue comme sortie. Par exemple:
- Prix (150$, 199$, 400$, etc.)
- Hauteur (14 pouces, 2 pieds, 94,32 centimètres, etc.)
- Âge (2 mois, 6 ans, 41,5 ans, etc.)
- Distance (1,23 miles, 4,5 kilomètres, etc.)
À l’inverse, la régression logistique prédit les probabilités comme résultat. Par exemple:
- 40,3% de chances d’être accepté dans une université.
- 93,2% de chances de gagner une partie.
- 34,2% de chances qu’une loi soit adoptée.
Quand utiliser la régression logistique ou linéaire
Les problèmes pratiques suivants peuvent vous aider à mieux comprendre quand utiliser la régression logistique ou la régression linéaire.
Problème n°1 : revenu annuel
Supposons qu’un économiste souhaite utiliser des variables prédictives (1) les heures hebdomadaires travaillées et (2) les années d’études pour prédire le revenu annuel des individus.
Dans ce scénario, il utiliserait la régression linéaire car la variable de réponse (revenu annuel) est continue.
Problème n°2 : acceptation universitaire
Supposons qu’un responsable des admissions dans un collège souhaite utiliser les variables prédictives (1) GPA et (2) score ACT pour prédire la probabilité qu’un étudiant soit accepté dans une certaine université.
Dans ce scénario, elle utiliserait la régression logistique car la variable de réponse est catégorielle et ne peut prendre que deux valeurs : acceptée ou non acceptée.
Problème n°3 : prix de l’immobilier
Supposons qu’un agent immobilier souhaite utiliser les variables prédictives (1) la superficie en pieds carrés, (2) le nombre de chambres et (3) le nombre de salles de bains pour prédire les prix de la maison de vente.
Dans ce scénario, elle utiliserait la régression linéaire car la variable de réponse (prix) est continue.
Problème n°4 : détection du spam
Supposons qu’un programmeur informatique souhaite utiliser les variables prédictives (1) nombre de mots et (2) pays d’origine pour prédire la probabilité qu’un e-mail donné soit du spam.
Dans ce scénario, il utiliserait la régression logistique car la variable de réponse est catégorique et ne peut prendre que deux valeurs : spam ou non spam.
Ressources additionnelles
Les didacticiels suivants offrent plus de détails sur la régression linéaire :
- Introduction à la régression linéaire simple
- Introduction à la régression linéaire multiple
- 4 exemples d’utilisation de la régression linéaire dans la vie réelle
Les didacticiels suivants offrent plus de détails sur la régression logistique :

