Une introduction à la distribution de Poisson

La distribution de Poisson est l’une des distributions les plus populaires en statistique.

Pour comprendre la distribution de Poisson, il est utile de d’abord comprendre les expériences de Poisson.

Expériences de Poisson

Une expérience de Poisson est une expérience qui possède les propriétés suivantes :

• Le nombre de réussites de l’expérience peut être compté.
• Le nombre moyen de succès survenus au cours d’un intervalle de temps (ou d’espace) spécifique est connu.
• Chaque résultat est indépendant.
• La probabilité qu’un succès se produise est proportionnelle à la taille de l’intervalle.

Un exemple d’expérience de Poisson est le nombre de naissances par heure dans un hôpital donné. Par exemple, supposons qu’un hôpital particulier enregistre en moyenne 10 naissances par heure. Il s’agit d’une expérience de Poisson car elle possède les quatre propriétés suivantes :

• Le nombre de réussites de l’expérience peut être compté – On peut compter le nombre de naissances.
• Le nombre moyen de réussites qui se produisent au cours d’un intervalle de temps spécifique est connu – On sait qu’il y a en moyenne 10 naissances par heure.
• Chaque résultat est indépendant – La probabilité qu’une mère accouche au cours d’une heure donnée est indépendante de la probabilité qu’une autre mère accouche.
• La probabilité qu’un succès se produise est proportionnelle à la taille de l’intervalle : plus l’intervalle de temps est long, plus la probabilité qu’une naissance se produise est élevée.

Nous pouvons utiliser la distribution de Poisson pour répondre à des questions sur les probabilités concernant cette expérience de Poisson telles que :

• Quelle est la probabilité que plus de 12 naissances aient lieu dans une heure donnée ?
• Quelle est la probabilité que moins de 5 naissances aient lieu dans une heure donnée ?
• Quelle est la probabilité qu’entre 8 et 11 naissances aient lieu dans une heure donnée ?

La distribution de Poisson

La distribution de Poisson décrit la probabilité d’obtenir k succès pendant un intervalle de temps donné.

Si une variable aléatoire X suit une distribution de Poisson, alors la probabilité que X = k succès peut être trouvée par la formule suivante :

P(X=k) = λ ^k * e ^{– λ} / k !

où:

• λ : nombre moyen de succès survenus au cours d’un intervalle spécifique
• k : nombre de réussites
• e : une constante égale à environ 2,71828

Par exemple, supposons qu’un hôpital particulier connaisse en moyenne 2 naissances par heure. Nous pouvons utiliser la formule ci-dessus pour déterminer la probabilité de connaître 0, 1, 2, 3 naissances, etc. dans une heure donnée :

P(X=0) = 2 ⁰ * e ^{– 2} / 0 ! = 0,1353

P(X=1) = 2 ¹ * e ^{– 2} / 1 ! = 0,2707

P(X=2) = 2 ² * e ^{– 2} / 2 ! = 0,2707

P(X=3) = 2 ³ * e ^{– 2} / 3 ! = 0,1805

Nous pouvons calculer la probabilité d’un nombre quelconque de naissances jusqu’à l’infini. Nous créons ensuite un histogramme simple pour visualiser cette distribution de probabilité :

Calcul des probabilités cumulées de Poisson

Il est simple de calculer une seule probabilité de Poisson (par exemple la probabilité qu’un hôpital connaisse 3 naissances au cours d’une heure donnée) en utilisant la formule ci-dessus, mais pour calculer les probabilités de Poisson cumulées, nous devons ajouter des probabilités individuelles.

Par exemple, supposons que nous souhaitions connaître la probabilité que l’hôpital connaisse 1 naissance ou moins au cours d’une heure donnée. Nous utiliserions la formule suivante pour calculer cette probabilité :

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

C’est ce qu’on appelle une probabilité cumulative car elle implique l’ajout de plusieurs probabilités. Nous pouvons calculer la probabilité cumulée de connaître k naissances ou moins au cours d’une heure donnée en utilisant une formule similaire :

P(X≤0) = P(X=0) = 0,1353

P(X≤1) = P(X=0) + P(X=1) = 0,1353 + 0,2707 = 0,406

P(X≤2) = P(X=0) + P(X=1) + P(X=2) =0,1353 + 0,2707 + 0,2707 = 0,6767

Nous pouvons calculer ces probabilités cumulées pour n’importe quel nombre de naissances jusqu’à l’infini. Nous pouvons ensuite créer un histogramme pour visualiser cette distribution de probabilité cumulée :

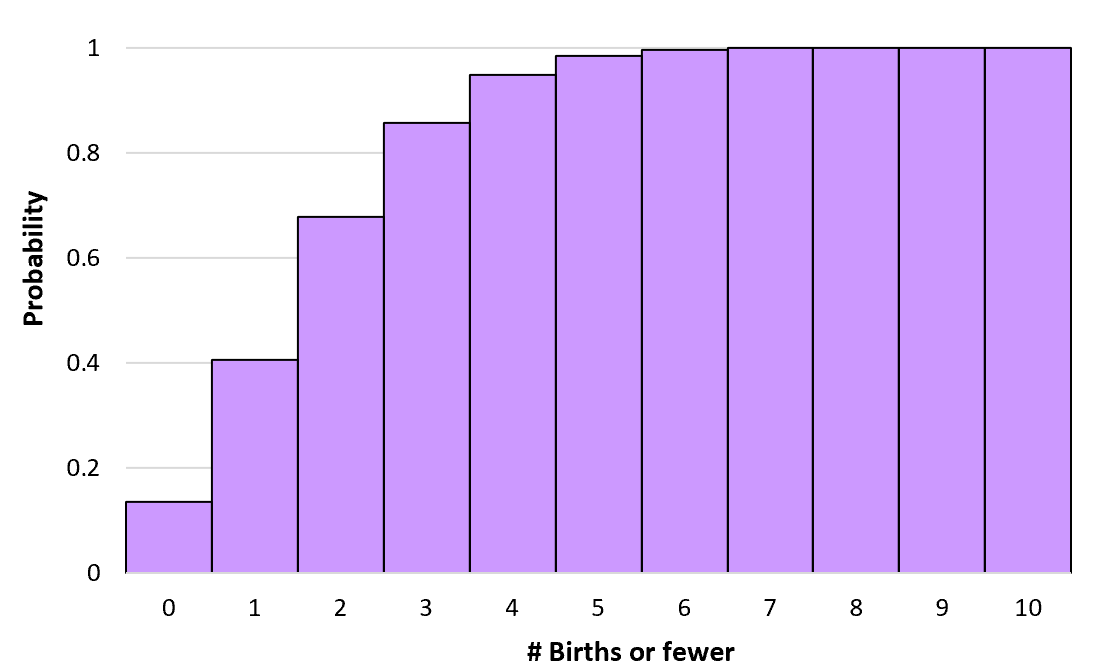
Propriétés de la distribution de Poisson

La distribution de Poisson a les propriétés suivantes :

La moyenne de la distribution est λ .

La variance de la distribution est également λ .

L’écart type de la distribution est √ λ .

Par exemple, supposons qu’un hôpital enregistre en moyenne 2 naissances par heure.

Le nombre moyen de naissances attendu dans une heure donnée est λ = 2 naissances.

La variance du nombre de naissances à laquelle nous nous attendons est λ = 2 naissances.

Problèmes de pratique de la distribution de Poisson

Utilisez les problèmes pratiques suivants pour tester vos connaissances de la distribution de Poisson.

Remarque : Nous utiliserons le calculateur de distribution de Poisson pour calculer les réponses à ces questions.

Problème 1

Question : On sait qu’un certain site Web réalise 10 ventes par heure. Dans une heure donnée, quelle est la probabilité que le site réalise exactement 8 ventes ?

Réponse : En utilisant le calculateur de distribution de Poisson avec λ = 10 et x = 8, nous trouvons que P(X=8) = 0,1126 .

Problème 2

Question : On sait qu’un certain agent immobilier réalise en moyenne 5 ventes par mois. Sur un mois donné, quelle est la probabilité qu’elle réalise plus de 7 ventes ?

Réponse : En utilisant le calculateur de distribution de Poisson avec λ = 5 et x = 7, nous trouvons que P(X>7) = 0,13337 .

Problème 3

Question : On sait qu’un certain hôpital connaît 4 accouchements par heure. Dans une heure donnée, quelle est la probabilité qu’il y ait 4 naissances ou moins ?

Réponse : En utilisant le calculateur de distribution de Poisson avec λ = 4 et x = 4, nous trouvons que P(X≤4) = 0,62884 .

Ressources additionnelles

Les articles suivants expliquent comment utiliser la distribution de Poisson dans différents logiciels statistiques :

Comment utiliser la distribution de Poisson dans R
Comment utiliser la distribution de Poisson dans Excel
Comment calculer les probabilités de Poisson sur une calculatrice TI-84
Exemples réels de la distribution de Poisson
Calculateur de distribution de Poisson