Qu’est-ce que la restriction de portée ?

Souvent, en statistiques, nous cherchons à mesurer la corrélation entre deux variables. Cela nous aide à comprendre les éléments suivants :

• La direction de la relation entre deux variables. À mesure qu’une variable augmente, l’autre variable a-t-elle tendance à augmenter ou à diminuer ?
• La force de la relation entre deux variables. Dans quelle mesure la valeur des deux variables change-t-elle ?

Malheureusement, un problème qui peut survenir lors de la mesure de la corrélation entre deux variables est appelé restriction de plage . Cela se produit lorsque la plage de valeurs mesurées pour l’une des variables est restreinte pour une raison quelconque.

Par exemple, supposons que nous souhaitions mesurer la corrélation entre les heures d’études et les résultats aux examens des élèves d’une école particulière.

Si nous collectons des données sur ces deux variables pour l’ensemble des 1 000 élèves de l’école, nous pourrions constater que la corrélation entre les heures étudiées et les résultats à l’examen est de 0,73 .

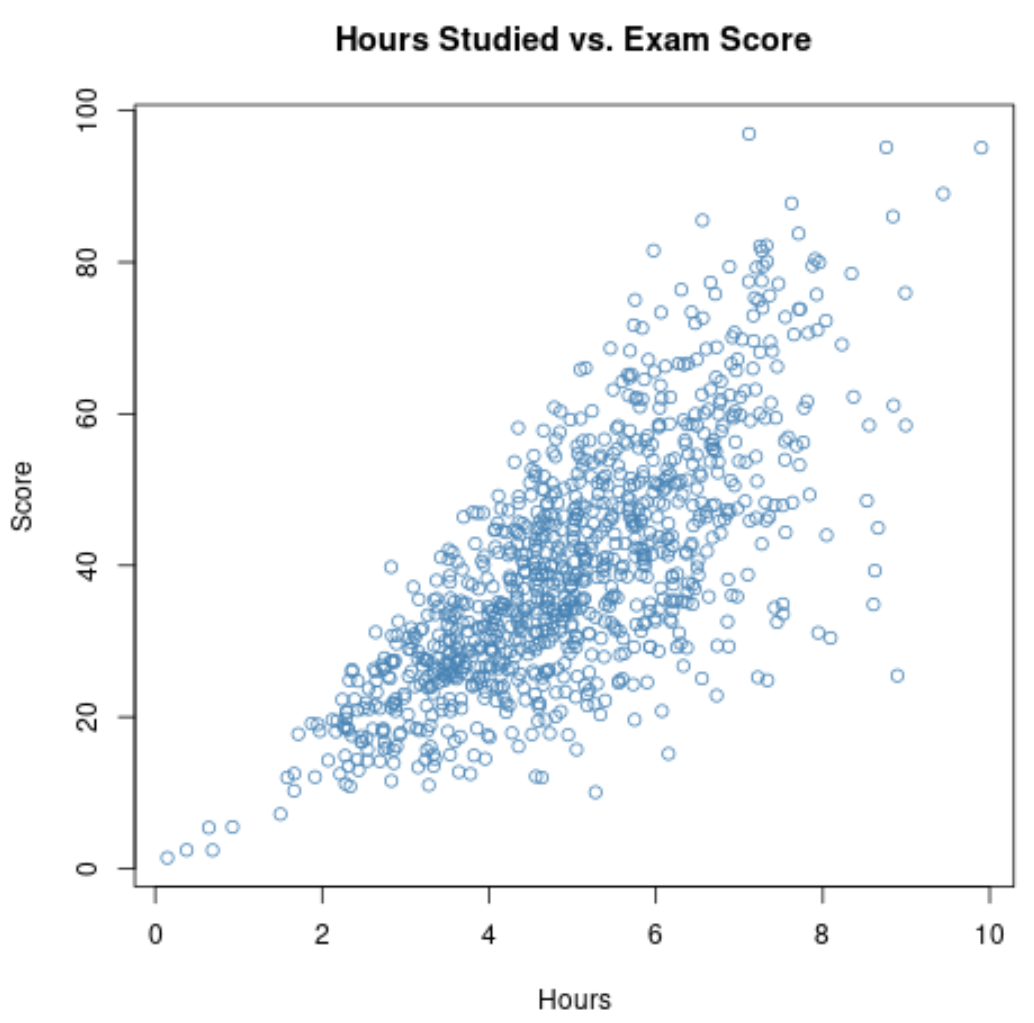
Cette corrélation est assez élevée, ce qui indique une forte relation positive entre les deux variables. À mesure que les étudiants étudient davantage, ils ont tendance à obtenir de meilleurs résultats aux examens.

Cependant, supposons que nous collections uniquement des données sur les étudiants des cours spécialisés. Il se pourrait que tous ces étudiants aient étudié pendant au moins 6 heures.

Ainsi, si nous calculons la corrélation entre les heures étudiées et les résultats aux examens de ces étudiants, nous utiliserions une plage restreinte pour les heures variables étudiées .

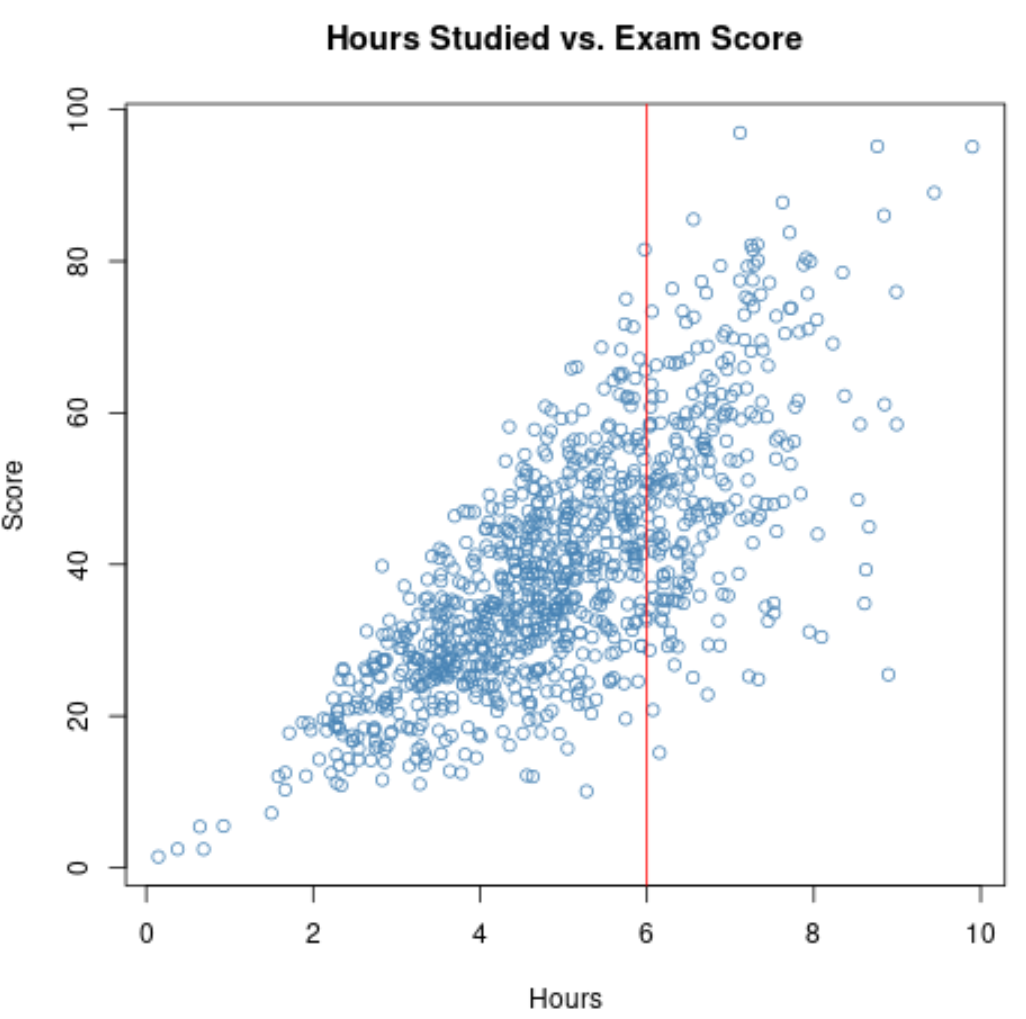
Si nous zoomons sur le nuage de points pour la plage où les heures sont supérieures à 6, voici à quoi ressemble le tracé :

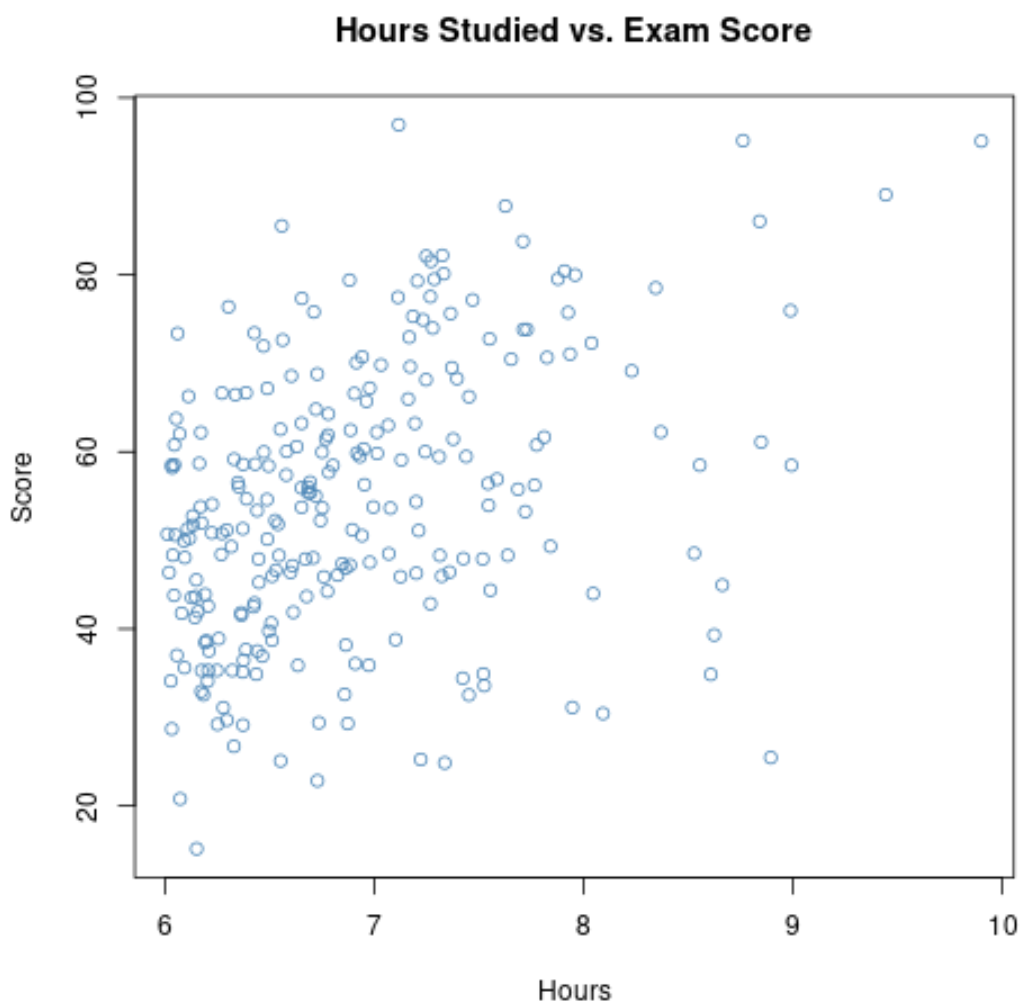
La corrélation entre les deux variables sur ce graphique s’avère être de 0,37 , ce qui est nettement inférieur à 0,73 .

Ainsi, si nous collections uniquement des données sur les heures étudiées et les résultats aux examens pour les étudiants des cours spécialisés, nous pourrions supposer qu’il existe une faible relation entre les heures étudiées et les résultats aux examens.

Cependant, ce résultat serait trompeur car nous avons utilisé une plage restreinte pour l’une des variables.

Exemples concrets de plage restreinte

Le problème d’une plage restreinte peut se poser dans la pratique dans de nombreuses études de recherche différentes. Voici quelques exemples :

1. Études sur les athlètes de haut niveau . Les chercheurs pourraient être intéressés à étudier si un certain programme d’entraînement produit plus de masse musculaire qu’un certain programme standard.

Si les chercheurs collectent uniquement des données sur les athlètes de haut niveau, il est probable que ces athlètes possèdent déjà tous une masse musculaire élevée. Il y aura donc une plage étroite de valeurs disponibles pour calculer la corrélation entre le programme d’entraînement et la masse musculaire produite.

2. Études d’étudiants performants. Les chercheurs pourraient vouloir étudier si un certain programme de tutorat a ou non un effet positif sur les notes. Par nature, les étudiants désireux d’améliorer leurs notes et de participer au programme de tutorat peuvent déjà être des étudiants très performants.

Il n’y a donc peut-être pas beaucoup de marge d’amélioration dans les notes de ces élèves. Lorsque les chercheurs calculent la corrélation entre les heures passées dans le programme de tutorat et l’augmentation des notes qui en résulte, la véritable corrélation peut être sous-estimée car la marge d’amélioration des notes a été restreinte.

Comment tenir compte des plages restreintes

Une façon populaire de prendre en compte les plages restreintes est connue sous le nom de Cas de Thorndike 2 , une formule développée par le psychométricien Robert L. Thorndike.

Cette formule fournit une estimation de la véritable corrélation entre deux variables et utilise le calcul suivant :

Corrélation vraie = √(1-(SD ² _{y restreint} -SD ² _{y sans restriction} )) * (1-r ² _restreint )

où:

• SD ² _{y restreint} : L’écart type carré des données disponibles sur la variable de réponse y.
• SD ² _{y sans restriction} : L’écart type carré connu de la variable de réponse pour la population.
• r ² _restreint : La corrélation quadratique sur les données restreintes disponibles.

Cette formule s’est avérée efficace pour produire des estimations impartiales de la véritable corrélation entre deux variables lorsque l’une des variables souffre d’une plage restreinte.

Notez que pour utiliser cette formule, vous devez disposer d’une estimation du véritable écart type de la population pour la variable de réponse.