Comment créer une matrice de corrélation dans SAS (avec exemple)

Une matrice de corrélation est un tableau carré qui montre les coefficients de corrélation entre les variables d’un ensemble de données.

Il offre un moyen rapide de comprendre la force des relations linéaires qui existent entre les variables d’un ensemble de données.

Vous pouvez utiliser l’instruction PROC CORR dans SAS pour créer une matrice de corrélation pour un ensemble de données donné :

/*create correlation matrix using all numeric variables in my_data*/
proc corr data=my_data;
run;

Par défaut, cela créera une matrice qui affiche les coefficients de corrélation entre toutes les variables numériques de l’ensemble de données.

Pour inclure uniquement des variables spécifiques dans la matrice de corrélation, vous pouvez utiliser l’instruction VAR :

/*create correlation matrix using only var1, var2 and var3 in my_data*/
proc corr data=my_data;
    var var1, var2, var3;
run;

L’exemple suivant montre comment créer une matrice de corrélation dans SAS.

Exemple : création d’une matrice de corrélation dans SAS

Supposons que nous ayons l’ensemble de données suivant dans SAS qui contient des informations sur divers joueurs de basket-ball :

/*create dataset*/
data my_data;
    input team $ assists rebounds points;
    datalines;
A 4 12 22
A 5 14 24
A 5 13 26
A 6 7 26
B 7 8 29
B 8 8 32
B 8 9 20
B 10 13 14
;
run;

/*view dataset*/
proc print data=my_data; 

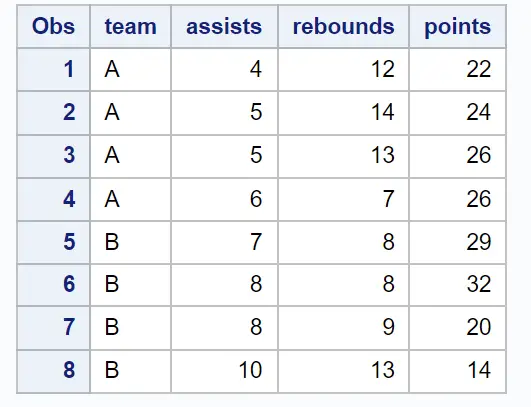
Nous pouvons utiliser l’instruction PROC CORR pour créer une matrice de corrélation qui inclut par défaut chaque variable numérique de l’ensemble de données :

/*create correlation matrix using all numeric variables in my_data*/
proc corr data=my_data;
run;

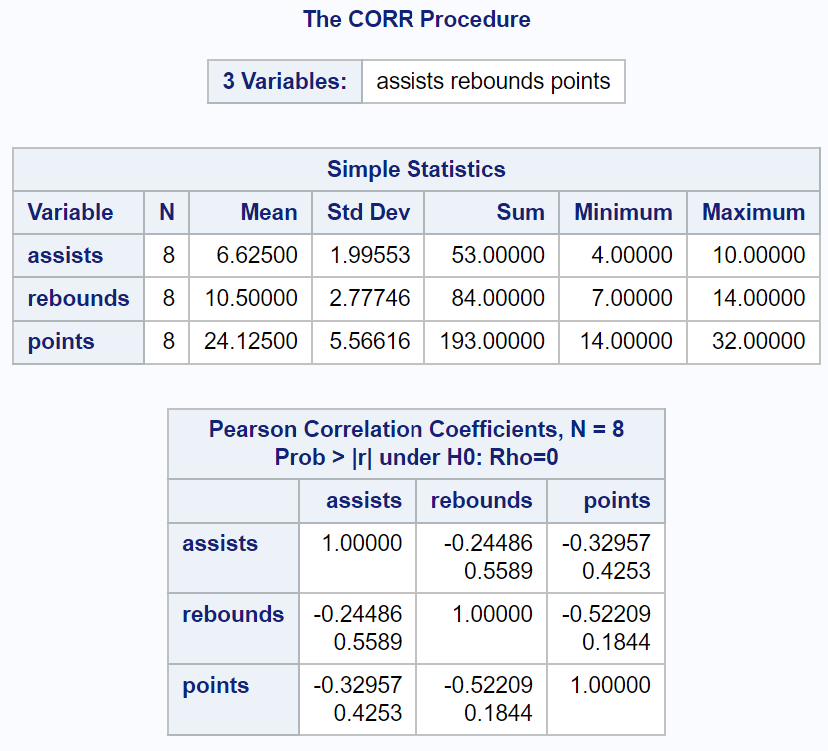
La sortie affiche des statistiques récapitulatives des variables numériques dans le premier tableau ainsi qu’une matrice de corrélation.

Notez que la variable « équipe » n’a pas été incluse dans la matrice de corrélation car il ne s’agissait pas d’une variable numérique.

Voici comment interpréter les valeurs de la matrice de corrélation :

(1) Le coefficient de corrélation de Pearson (r) entre passes décisives et rebonds est de -0,24486 . La valeur p correspondante est de 0,5589 .

Puisque r est inférieur à zéro, cela nous indique qu’il existe une association linéaire négative entre ces deux variables. Cependant, la valeur p n’est pas inférieure à 0,05, cette corrélation n’est donc pas statistiquement significative.

(2) Le coefficient de corrélation de Pearson (r) entre les passes décisives et les points est de -0,32957 . La valeur p correspondante est de 0,4253 .

Il existe une association linéaire négative entre ces deux variables mais elle n’est pas statistiquement significative.

(3) Le coefficient de corrélation de Pearson (r) entre rebonds et points est de -0,52209 . La valeur p correspondante est de 0,1844 .

Il existe une association linéaire négative entre ces deux variables mais elle n’est pas statistiquement significative.

Notez que nous pourrions également utiliser l’instruction VAR pour inclure uniquement des variables numériques spécifiques dans la matrice de corrélation :

/*create correlation matrix using only assists and rebounds variables*/
proc corr data=my_data;
    var assists rebounds;
run;

Notez que seules les variables de passes décisives et de rebonds ont été incluses dans cette matrice de corrélation.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment créer une matrice de nuages de points dans SAS
Comment créer des tableaux croisés dynamiques dans SAS
Comment calculer le facteur d’inflation de variance (VIF) dans SAS