Comment effectuer une régression linéaire simple dans SAS

La régression linéaire simple est une technique que nous pouvons utiliser pour comprendre la relation entre une variable prédictive et une variable de réponse .

Cette technique trouve une ligne qui « correspond » le mieux aux données et prend la forme suivante :

ŷ = b ₀ + b ₁ x

où:

• ŷ : La valeur de réponse estimée
• b ₀ : L’origine de la droite de régression
• b ₁ : La pente de la droite de régression

Cette équation nous aide à comprendre la relation entre la variable prédictive et la variable de réponse.

L’exemple étape par étape suivant montre comment effectuer une régression linéaire simple dans SAS.

Étape 1 : Créer les données

Pour cet exemple, nous allons créer un ensemble de données contenant le nombre total d’heures étudiées et la note de l’examen final de 15 étudiants.

Nous allons ajuster un modèle de régression linéaire simple en utilisant les heures comme variable prédictive et le score comme variable de réponse.

Le code suivant montre comment créer cet ensemble de données dans SAS :

/*create dataset*/
data exam_data;
    input hours score;
    datalines;
1 64
2 66
4 76
5 73
5 74
6 81
6 83
7 82
8 80
10 88
11 84
11 82
12 91
12 93
14 89
;
run;

/*view dataset*/
proc print data=exam_data;

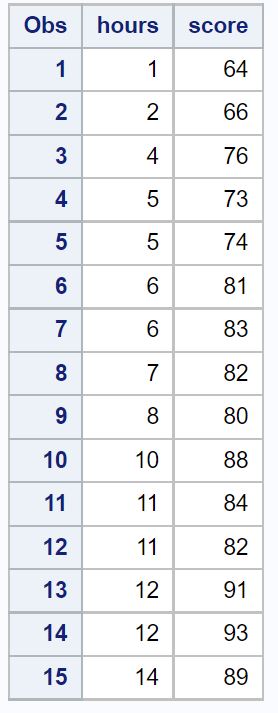
Étape 2 : Ajuster le modèle de régression linéaire simple

Ensuite, nous utiliserons proc reg pour ajuster le modèle de régression linéaire simple :

/*fit simple linear regression model*/
proc reg data=exam_data;
   model score = hours;
run;

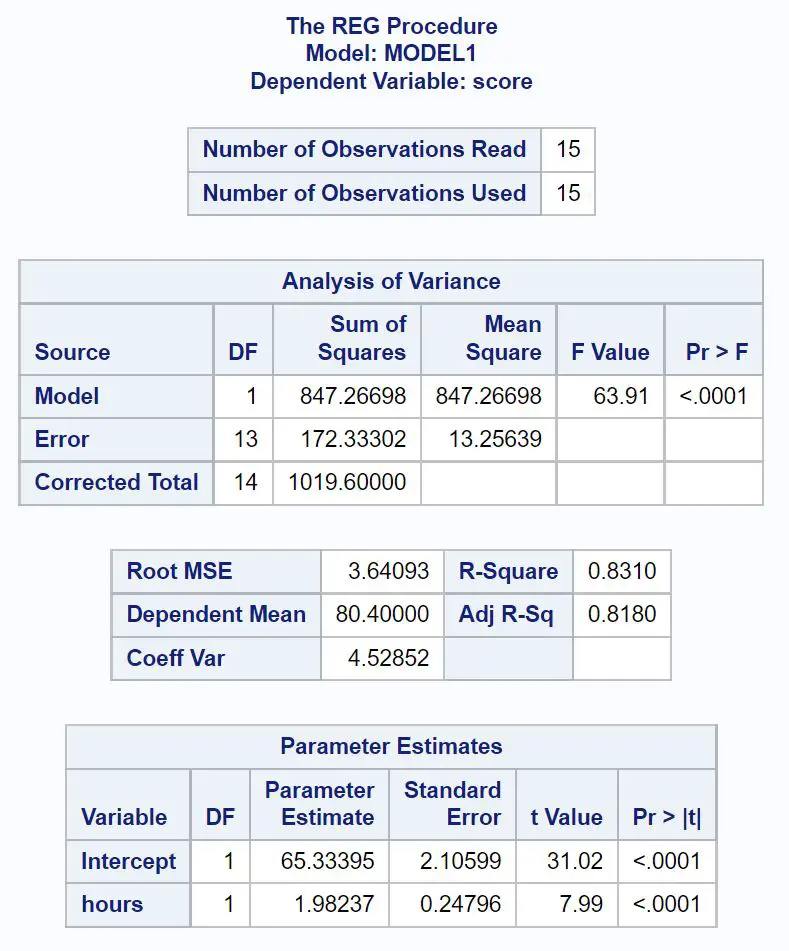
Voici comment interpréter les valeurs les plus importantes de chaque tableau dans le résultat :

Tableau d’analyse des écarts :

La valeur F globale du modèle de régression est de 63,91 et la valeur p correspondante est <0,0001 .

Puisque cette valeur p est inférieure à 0,05, nous concluons que le modèle de régression dans son ensemble est statistiquement significatif. En d’autres termes, les heures sont une variable utile pour prédire les résultats à l’examen.

Tableau d’ajustement du modèle :

La valeur R-Carré nous indique le pourcentage de variation des résultats des examens qui peut s’expliquer par le nombre d’heures étudiées.

En général, plus la valeur R au carré d’un modèle de régression est grande, plus les variables prédictives sont capables de prédire la valeur de la variable de réponse.

Dans ce cas, 83,1 % de la variation des résultats aux examens peut s’expliquer par le nombre d’heures étudiées. Cette valeur est assez élevée, ce qui indique que les heures étudiées sont une variable très utile pour prédire les résultats à l’examen.

Tableau des estimations des paramètres :

À partir de ce tableau, nous pouvons voir l’équation de régression ajustée :

Score = 65,33 + 1,98*(heures)

Nous interprétons cela comme signifiant que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de 1,98 points de la note à l’examen.

La valeur d’origine nous indique que la note moyenne à l’examen pour un étudiant qui étudie zéro heure est de 65,33 .

Nous pouvons également utiliser cette équation pour trouver la note attendue à l’examen en fonction du nombre d’heures qu’un étudiant étudie.

Par exemple, un étudiant qui étudie pendant 10 heures devrait obtenir une note à l’examen de 85,13 :

Note = 65,33 + 1,98*(10) = 85,13

Étant donné que la valeur p (<0,0001) pour les heures est inférieure à 0,05 dans ce tableau, nous concluons qu’il s’agit d’une variable prédictive statistiquement significative.

Étape 3 : Analyser les tracés résiduels

La régression linéaire simple fait deux hypothèses importantes concernant les résidus du modèle :

• Les résidus sont normalement distribués.
• Les résidus ont une variance égale (« homoscédasticité ») à chaque niveau de la variable prédictive.

Si ces hypothèses ne sont pas respectées, les résultats de notre modèle de régression peuvent alors ne pas être fiables.

Pour vérifier que ces hypothèses sont remplies, nous pouvons analyser les tracés résiduels que SAS affiche automatiquement dans la sortie :

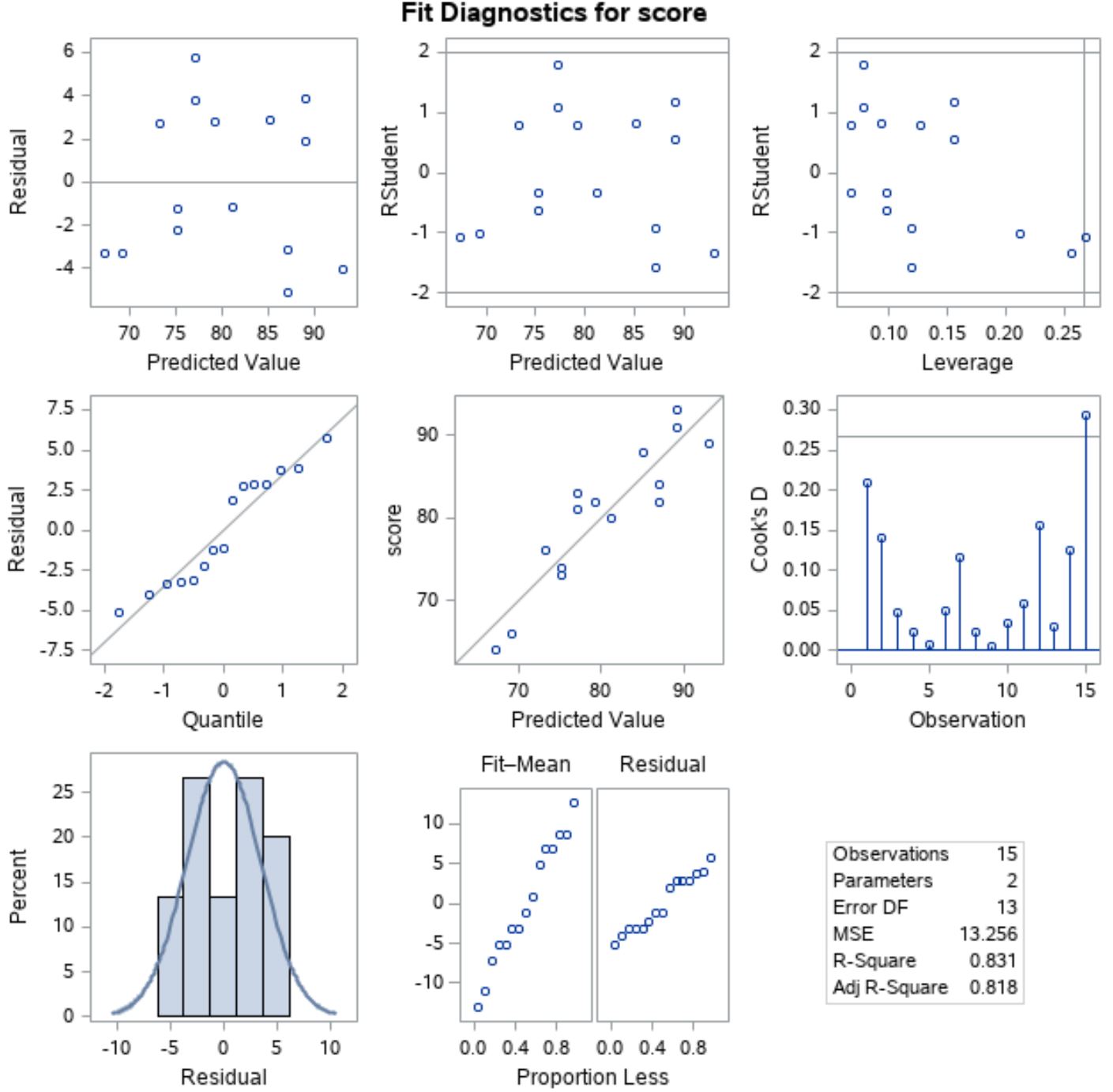
Pour vérifier que les résidus sont normalement distribués , nous pouvons analyser le tracé en position gauche de la ligne du milieu avec « Quantile » le long de l’axe des x et « Résiduel » le long de l’axe des y.

Ce tracé est appelé tracé QQ , abréviation de « quantile-quantile », et est utilisé pour déterminer si les données sont normalement distribuées ou non. Si les données sont distribuées normalement, les points d’un tracé QQ se trouveront sur une ligne diagonale droite.

Sur le graphique, nous pouvons voir que les points se situent à peu près le long d’une ligne diagonale droite, nous pouvons donc supposer que les résidus sont normalement distribués.

Ensuite, pour vérifier que les résidus sont homoscédastiques , nous pouvons regarder le tracé en position gauche de la première ligne avec « Valeur prédite » le long de l’axe des x et « Résiduel » le long de l’axe des y.

Si les points du tracé sont dispersés de manière aléatoire autour de zéro sans motif clair, nous pouvons alors supposer que les résidus sont homoscédastiques.

À partir du tracé, nous pouvons voir que les points sont dispersés autour de zéro de manière aléatoire avec une variance à peu près égale à chaque niveau tout au long du tracé, nous pouvons donc supposer que les résidus sont homoscédastiques.

Puisque les deux hypothèses sont remplies, nous pouvons supposer que les résultats du modèle de régression linéaire simple sont fiables.

Ressources additionnelles

Les didacticiels suivants expliquent comment effectuer d’autres tâches courantes dans SAS :

Comment effectuer une ANOVA unidirectionnelle dans SAS
Comment effectuer une ANOVA bidirectionnelle dans SAS
Comment calculer la corrélation dans SAS