Standardisation ou normalisation : quelle est la différence ?
La standardisation et la normalisation sont deux façons de redimensionner les données.
La normalisation redimensionne un ensemble de données pour avoir une moyenne de 0 et un écart type de 1. Pour ce faire, elle utilise la formule suivante :
x nouveau = (x je – x ) / s
où:
- x i : la ième valeur de l’ensemble de données
- x : La moyenne de l’échantillon
- s : l’écart type de l’échantillon
La normalisation redimensionne un ensemble de données afin que chaque valeur soit comprise entre 0 et 1. Pour ce faire, elle utilise la formule suivante :
x nouveau = (x je – x min ) / (x max – x min )
où:
- x i : la ième valeur de l’ensemble de données
- x min : La valeur minimale dans l’ensemble de données
- x max : La valeur maximale dans l’ensemble de données
Les exemples suivants montrent comment standardiser et normaliser un ensemble de données dans la pratique.
Exemple : Comment standardiser les données
Supposons que nous ayons l’ensemble de données suivant :
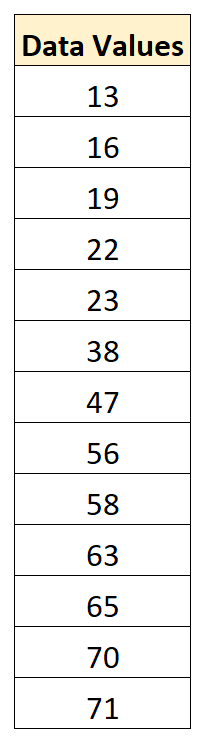
La valeur moyenne dans l’ensemble de données est de 43,15 et l’écart type est de 22,13.
Pour normaliser la première valeur de 13 , nous appliquerions la formule partagée précédemment :
- x nouveau = (x je – x ) / s = (13 – 43,15) / 22,13 = -1,36
Pour normaliser la deuxième valeur de 16 , nous utiliserions la même formule :
- x nouveau = (x je – x ) / s = (16 – 43,15) / 22,13 = -1,23
Pour normaliser la troisième valeur de 19 , nous utiliserions la même formule :
- x nouveau = (x je – x ) / s = (19 – 43,15) / 22,13 = -1,09
Nous pouvons utiliser exactement cette même formule pour standardiser chaque valeur de l’ensemble de données d’origine :
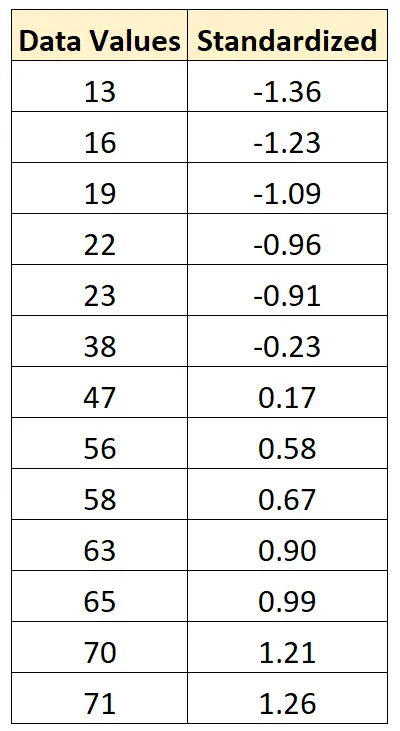
Exemple : Comment normaliser les données
Encore une fois, supposons que nous ayons l’ensemble de données suivant :

La valeur minimale dans l’ensemble de données est 13 et la valeur maximale est 71.
Pour normaliser la première valeur de 13 , nous appliquerions la formule partagée précédemment :
- x nouveau = (x i – x min ) / (x max – x min ) = (13 – 13) / (71 – 13) = 0
Pour normaliser la deuxième valeur de 16 , nous utiliserions la même formule :
- x nouveau = (x i – x min ) / (x max – x min ) = (16 – 13) / (71 – 13) = 0,0517
Pour normaliser la troisième valeur de 19 , nous utiliserions la même formule :
- x nouveau = (x i – x min ) / (x max – x min ) = (19 – 13) / (71 – 13) = 0,1034
Nous pouvons utiliser exactement cette même formule pour normaliser chaque valeur de l’ensemble de données d’origine entre 0 et 1 :
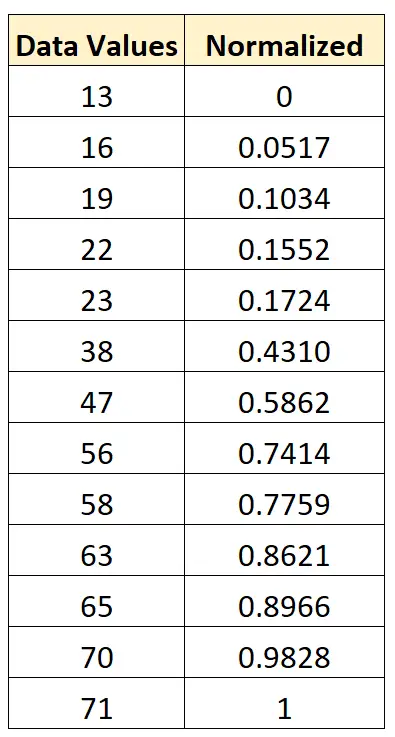
Standardisation ou normalisation : quand les utiliser ?
En règle générale, nous normalisons les données lorsque nous effectuons un certain type d’analyse dans laquelle nous avons plusieurs variables mesurées à différentes échelles et nous souhaitons que chacune des variables ait la même plage.
Cela évite qu’une variable ait une influence excessive, surtout si elle est mesurée dans des unités différentes (c’est-à-dire si une variable est mesurée en pouces et une autre en yards).
D’un autre côté, nous normalisons généralement les données lorsque nous souhaitons savoir à combien d’écarts types chaque valeur d’un ensemble de données se trouve par rapport à la moyenne.
Par exemple, nous pourrions avoir une liste des résultats des examens de 500 étudiants dans une école particulière et nous aimerions savoir à combien d’écarts types chaque résultat d’examen se trouve par rapport au score moyen.
Dans ce cas, nous pourrions normaliser les données brutes pour connaître cette information. Ensuite, un score standardisé de 1,26 nous indiquerait que le score à l’examen de cet étudiant particulier se situe 1,26 écarts-types au-dessus du score moyen à l’examen.
Que vous décidiez de normaliser ou de standardiser vos données, gardez les points suivants à l’esprit :
- Un ensemble de données normalisé aura toujours des valeurs comprises entre 0 et 1.
- Un ensemble de données standardisé aura une moyenne de 0 et un écart type de 1, mais il n’y a pas de limite supérieure ou inférieure spécifique pour les valeurs maximales et minimales.
Selon votre scénario particulier, il peut être plus judicieux de normaliser ou de standardiser les données.
Ressources additionnelles
Les tutoriels suivants expliquent comment standardiser et normaliser les données dans différents logiciels statistiques :
Comment normaliser les données dans R
Comment normaliser les données dans Excel
Comment normaliser les données en Python
Comment standardiser les données dans R
