Comment effectuer une régression hiérarchique dans Stata

La régression hiérarchique est une technique que nous pouvons utiliser pour comparer plusieurs modèles linéaires différents.

L’idée de base est que nous ajustons d’abord un modèle de régression linéaire avec une seule variable explicative. Ensuite, nous ajustons un autre modèle de régression en utilisant une variable explicative supplémentaire. Si le R-carré (la proportion de variance de la variable de réponse qui peut être expliquée par les variables explicatives) dans le deuxième modèle est significativement plus élevé que le R-carré dans le modèle précédent, cela signifie que le deuxième modèle est meilleur.

Nous répétons ensuite le processus d’ajustement de modèles de régression supplémentaires avec davantage de variables explicatives et voyons si les modèles les plus récents offrent une amélioration par rapport aux modèles précédents.

Ce didacticiel fournit un exemple de la façon d’effectuer une régression hiérarchique dans Stata.

Exemple : régression hiérarchique dans Stata

Nous utiliserons un ensemble de données intégré appelé auto pour illustrer comment effectuer une régression hiérarchique dans Stata. Tout d’abord, chargez l’ensemble de données en tapant ce qui suit dans la zone de commande :

utilisation automatique du système

Nous pouvons obtenir un résumé rapide des données en utilisant la commande suivante :

résumer

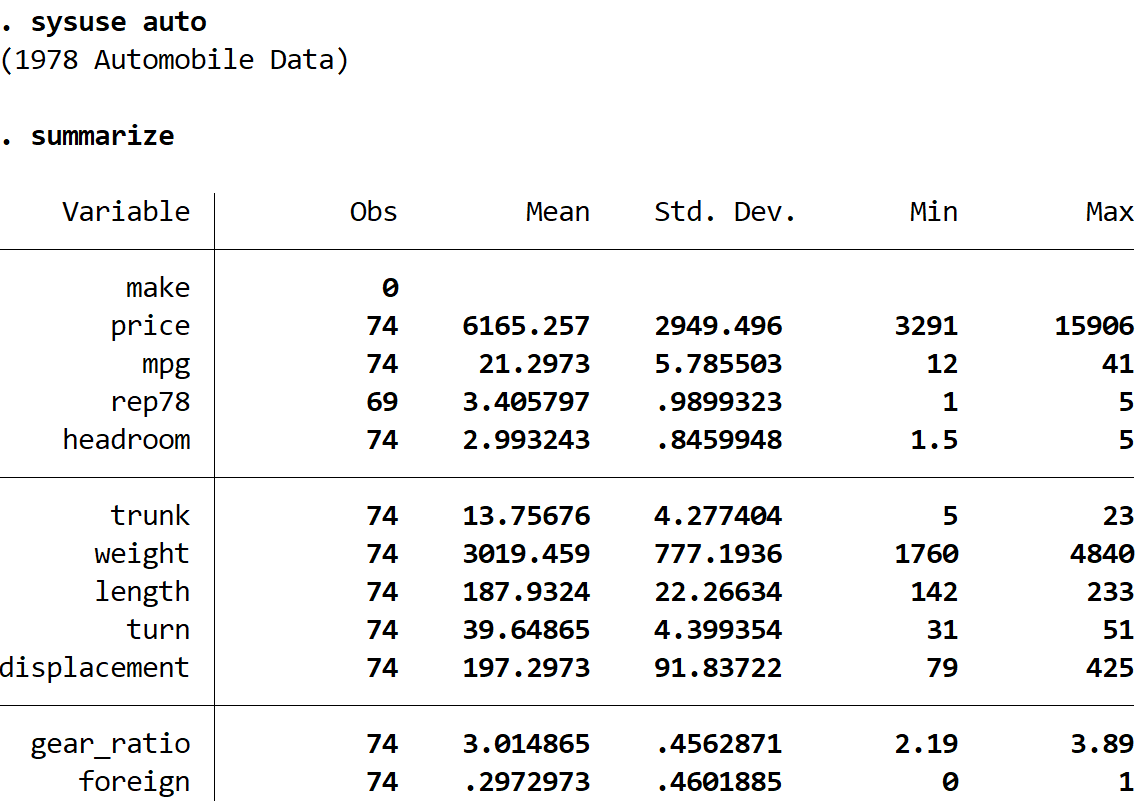
Nous pouvons voir que l’ensemble de données contient des informations sur 12 variables différentes pour 74 voitures au total.

Nous ajusterons les trois modèles de régression linéaire suivants et utiliserons la régression hiérarchique pour voir si chaque modèle suivant apporte ou non une amélioration significative par rapport au modèle précédent :

Modèle 1 : prix = interception + mpg

Modèle 2 : prix = interception + mpg + poids

Modèle 3 : prix = interception + mpg + poids + rapport de démultiplication

Afin d’effectuer une régression hiérarchique dans Stata, nous devrons d’abord installer le package Hireg . Pour ce faire, tapez ce qui suit dans la zone Commande :

trouver Hireg

Dans la fenêtre qui apparaît, cliquez sur Hireg depuis https://fmwww.bc.edu/RePEc/bocode/h

Dans la fenêtre suivante, cliquez sur le lien indiquant cliquez ici pour installer .

Le package s’installera en quelques secondes. Ensuite, pour effectuer une régression hiérarchique, nous utiliserons la commande suivante :

prix de location (mpg) (poids) (gear_ratio)

Voici ce que cela demande à Stata de faire :

• Effectuez une régression hiérarchique en utilisant le prix comme variable de réponse dans chaque modèle.
• Pour le premier modèle, utilisez mpg comme variable explicative.
• Pour le deuxième modèle, ajoutez du poids comme variable explicative supplémentaire.
• Pour le troisième modèle, ajoutez gear_ratio comme autre variable explicative.

Voici le résultat du premier modèle :

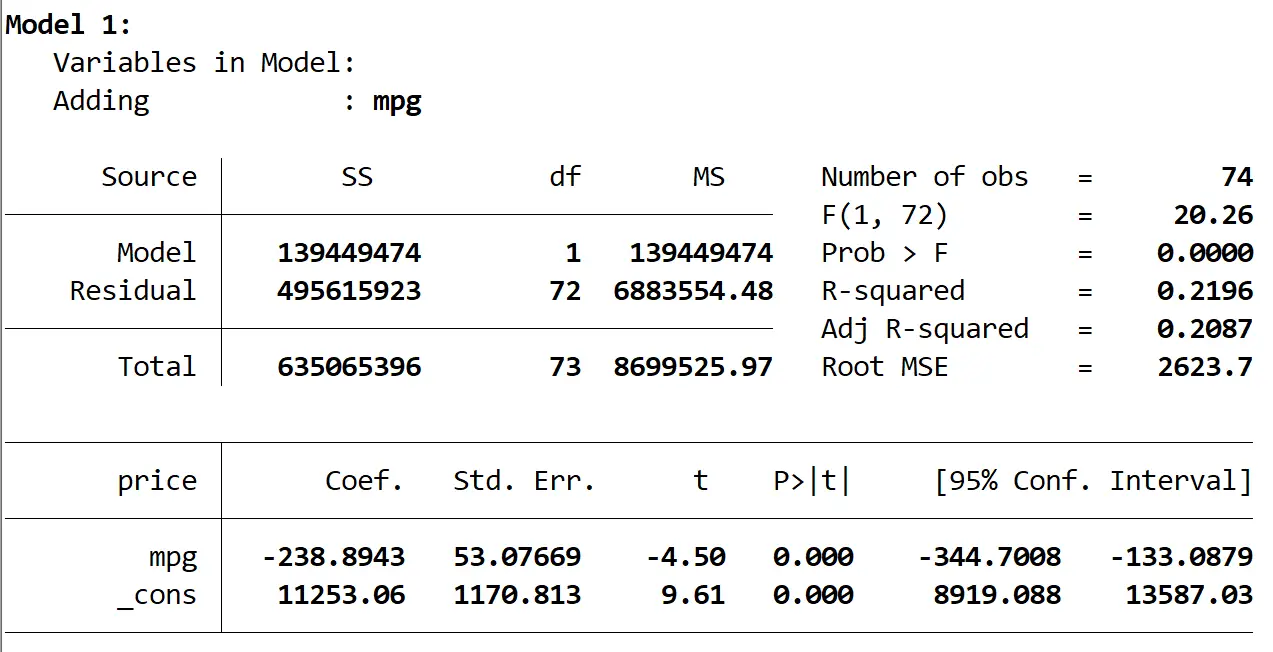
Nous voyons que le R au carré du modèle est de 0,2196 et la valeur p globale (Prob > F) du modèle est de 0,0000 , ce qui est statistiquement significatif à α = 0,05.

Ensuite, nous voyons le résultat du deuxième modèle :

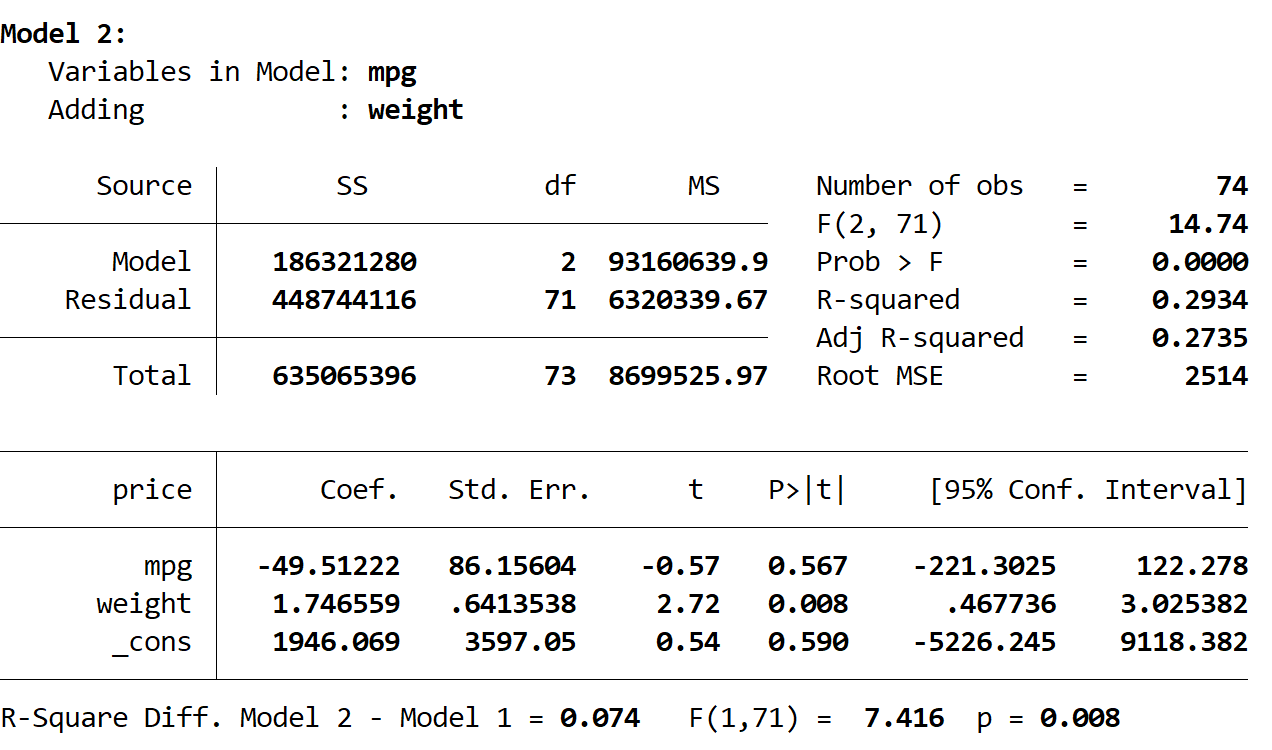
Le R carré de ce modèle est de 0,2934 , ce qui est plus grand que celui du premier modèle. Pour déterminer si cette différence est statistiquement significative, Stata a effectué un test F qui a donné les chiffres suivants au bas du résultat :

• Différence R au carré entre les deux modèles = 0,074
• Statistique F pour la différence = 7,416
• Valeur p correspondante de la statistique F = 0,008

La valeur p étant inférieure à 0,05, nous concluons qu’il existe une amélioration statistiquement significative dans le deuxième modèle par rapport au premier modèle.

Enfin, nous pouvons voir le résultat du troisième modèle :

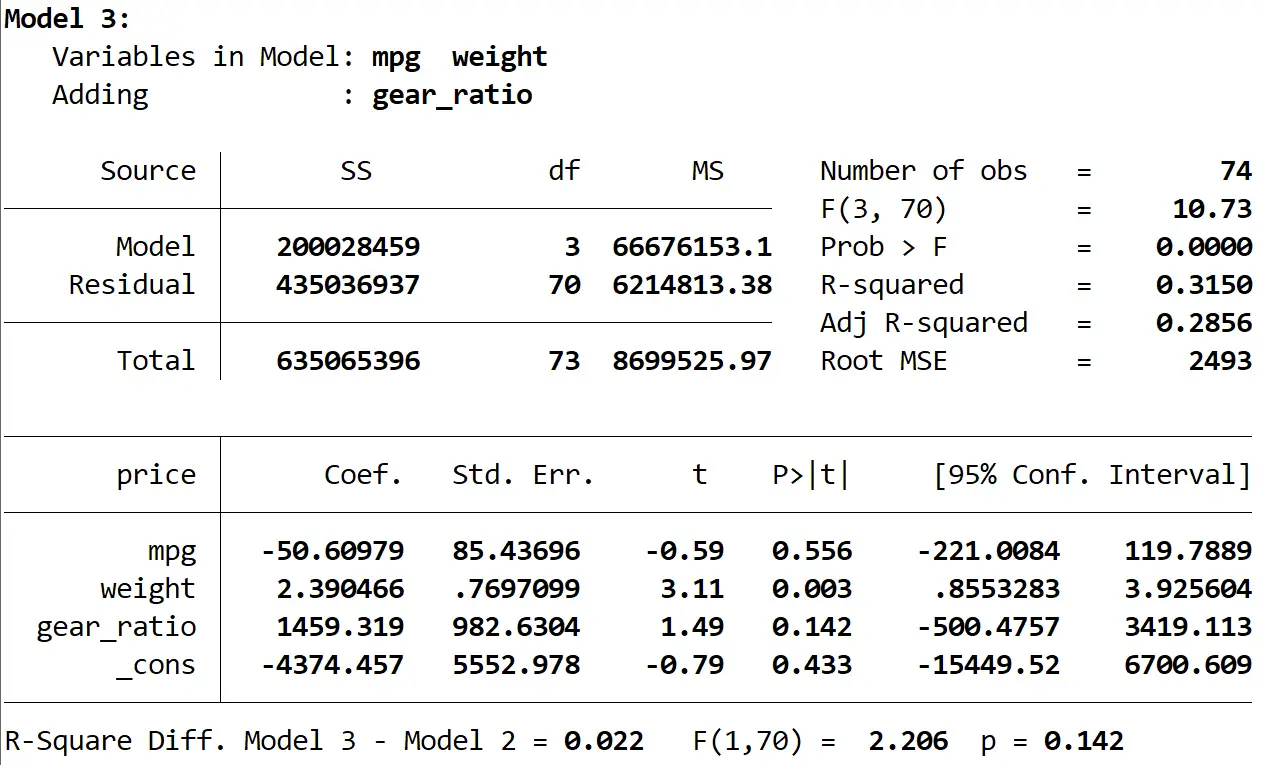
Le R carré de ce modèle est de 0,3150 , ce qui est plus grand que celui du deuxième modèle. Pour déterminer si cette différence est statistiquement significative, Stata a effectué un test F qui a donné les chiffres suivants au bas du résultat :

• Différence R au carré entre les deux modèles = 0,022
• Statistique F pour la différence = 2,206
• Valeur p correspondante de la statistique F = 0,142

Étant donné que la valeur p n’est pas inférieure à 0,05, nous ne disposons pas de preuves suffisantes pour affirmer que le troisième modèle offre une amélioration par rapport au deuxième modèle.

À la toute fin du résultat, nous pouvons voir que Stata fournit un résumé des résultats :

Dans cet exemple particulier, nous conclurions que le modèle 2 offrait une amélioration significative par rapport au modèle 1, mais que le modèle 3 n’offrait pas d’amélioration significative par rapport au modèle 2.