Blocage dans les statistiques : définition & Exemple

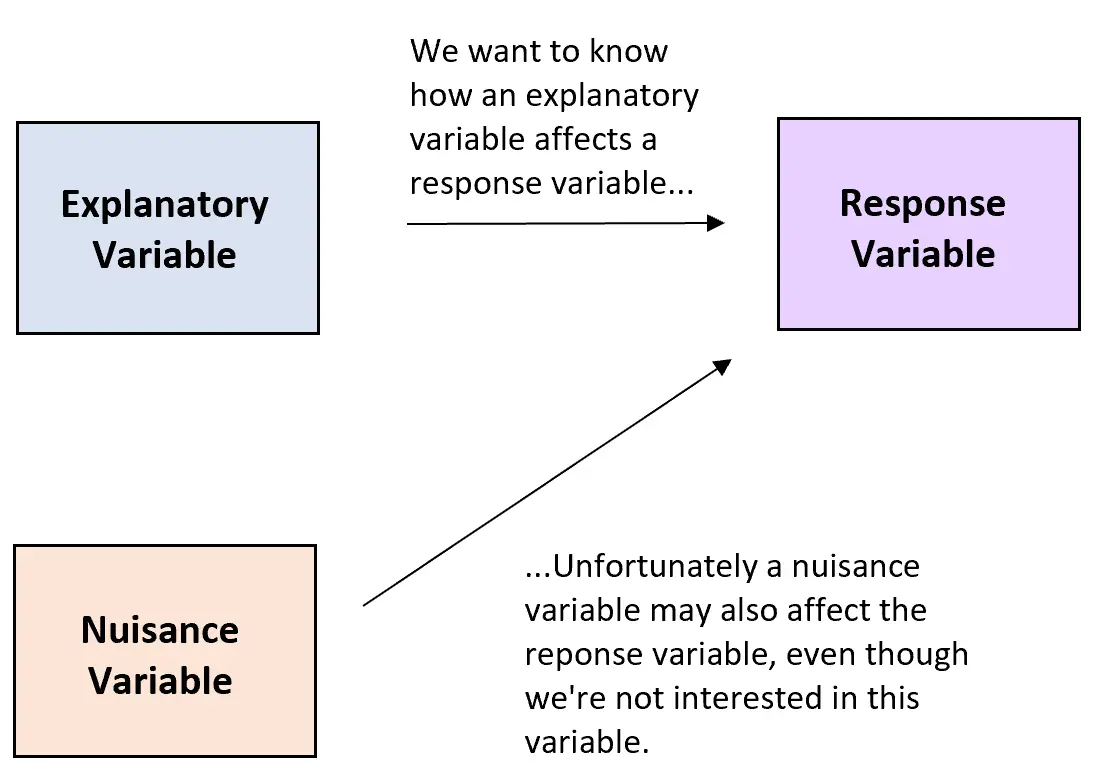
Souvent, dans les expériences, les chercheurs souhaitent comprendre la relation entre une variable explicative et une variable de réponse .

Malheureusement, des variables nuisibles apparaissent souvent dans les études expérimentales, qui sont des variables qui affectent la relation entre la variable explicative et la variable de réponse mais qui n’intéressent pas les chercheurs.

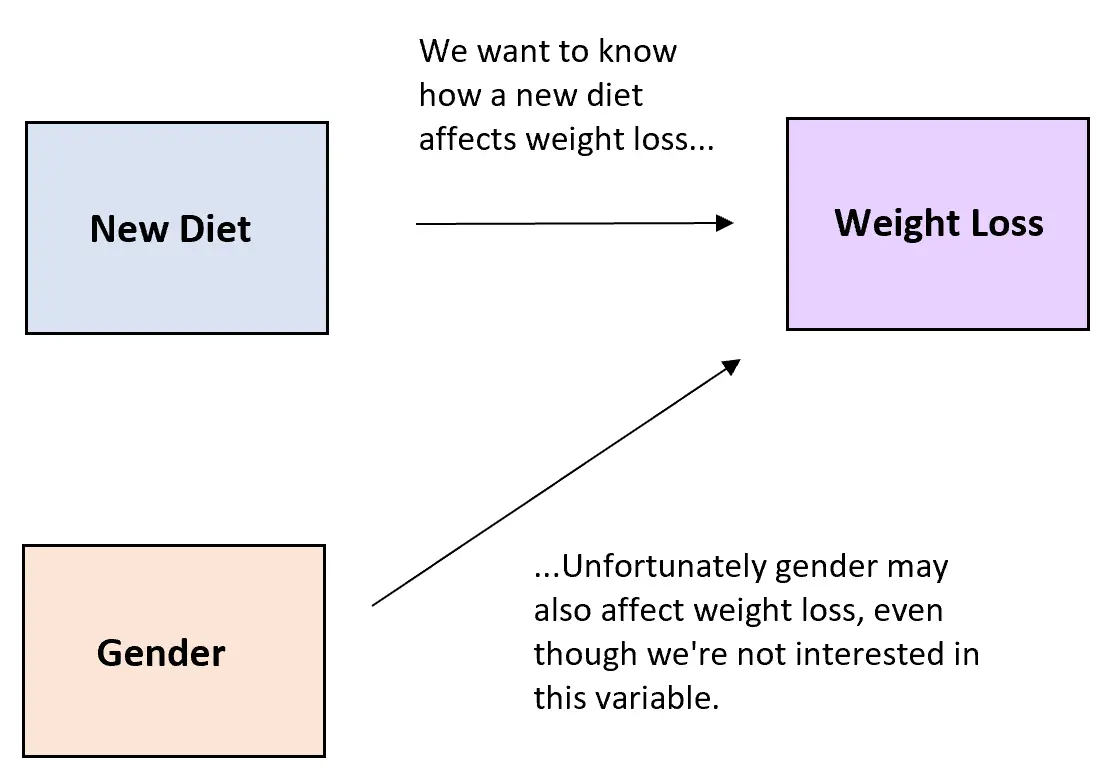
Par exemple, supposons que les chercheurs souhaitent comprendre l’effet d’un nouveau régime sur la perte de poids. La variable explicative est le nouveau régime alimentaire et la variable de réponse est le degré de perte de poids.

Cependant, une variable gênante susceptible de provoquer des variations est le sexe . Il est probable que le sexe d’un individu aura une incidence sur la quantité de poids qu’il perdra, que le nouveau régime fonctionne ou non.

Présentation du blocage

Une façon courante de contrôler l’effet des variables nuisibles consiste à bloquer , ce qui implique de diviser les individus dans une expérience basée sur la valeur d’une variable nuisible.

Dans notre exemple précédent, nous placerions les individus dans l’un des deux blocs suivants :

• Mâle
• Femelle

Ensuite, au sein de chaque bloc, nous assignerions au hasard les individus à l’un des deux traitements suivants :

• Un nouveau régime
• Un régime standard

En faisant cela, la variation au sein de chaque bloc serait bien inférieure à la variation entre tous les individus et nous serions en mesure de mieux comprendre comment le nouveau régime affecte la perte de poids tout en contrôlant le sexe.

Pour illustrer cela, considérons le tableau suivant qui montre la perte de poids totale de 16 personnes participant à l’étude :

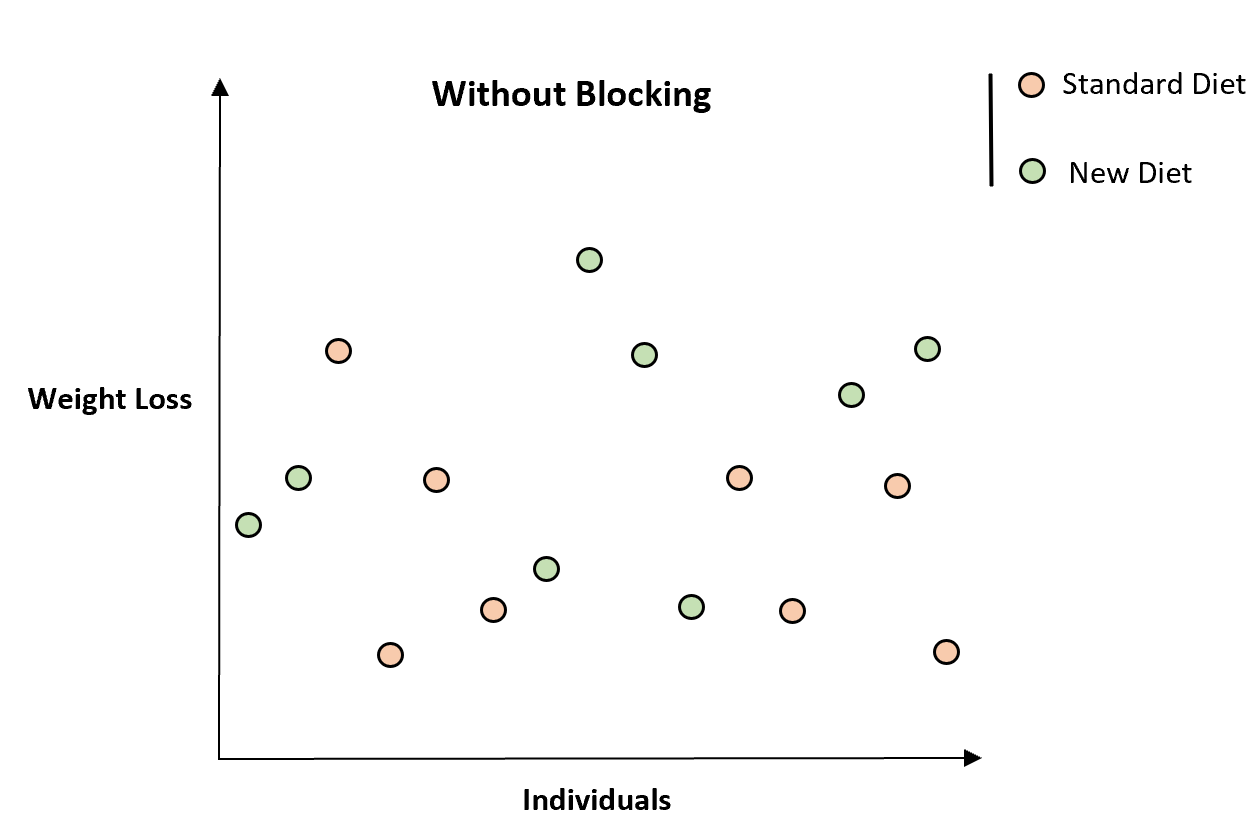
À première vue, il ne semble pas que le nouveau régime soit associé à une perte de poids accrue.

Cependant, une fois que nous avons divisé les individus en deux blocs en fonction du sexe, il devient évident que le nouveau régime semble être associé à une perte de poids accrue :

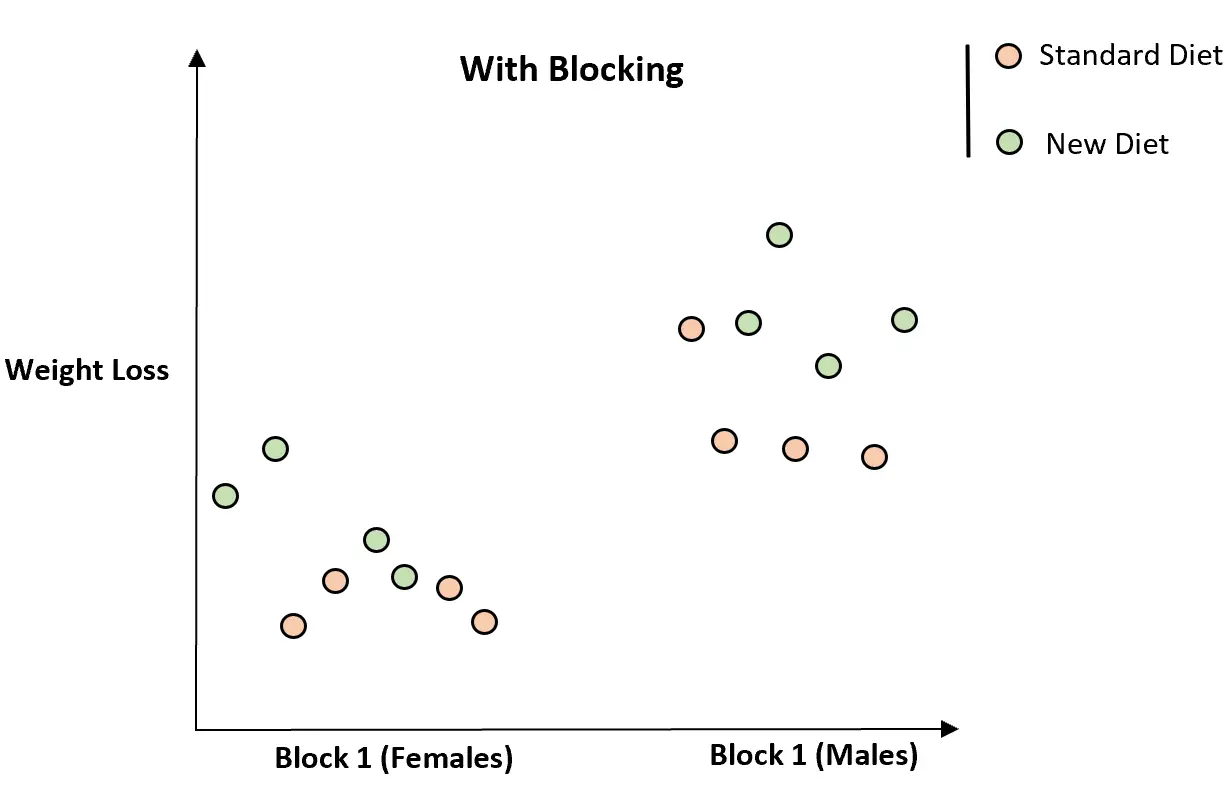
En plaçant les individus en blocs, la relation entre le nouveau régime et la perte de poids est devenue plus claire puisque nous avons pu contrôler la variable gênante du sexe.

Plus d’exemples de blocage

Le sexe est une variable gênante courante à utiliser comme facteur bloquant dans les expériences, car les hommes et les femmes ont tendance à réagir différemment à une grande variété de traitements.

Cependant, d’autres variables de nuisance courantes qui peuvent être utilisées comme facteurs bloquants comprennent :

• Tranche d’âge
• Groupe de revenu
• Niveau d’éducation
• Quantité d’exercice
• Région

Selon la nature de l’expérience, il est également possible d’utiliser plusieurs facteurs bloquants à la fois. Cependant, dans la pratique, seuls un ou deux sont généralement utilisés, car davantage de facteurs bloquants nécessitent des échantillons de plus grande taille pour obtenir des résultats significatifs.

Variables nuisibles et variables cachées

Dans l’exemple précédent, le sexe était une variable gênante connue qui, selon les chercheurs, affectait la perte de poids. Cependant, souvent dans les expériences, il y a aussi des variables cachées , qui sont des variables qui affectent également la relation entre une variable explicative et une variable de réponse, mais qui sont soit inconnues, soit tout simplement non incluses dans l’étude car il est difficile de collecter des données à leur sujet.

Par exemple, supposons que chaque individu possède une certaine discipline innée sur laquelle il peut s’appuyer pour perdre plus de poids. Étant donné que la discipline est difficile à mesurer, elle n’est pas incluse comme facteur bloquant dans l’étude, mais une façon de la contrôler est d’utiliser la randomisation .

En assignant au hasard des individus au nouveau régime ou au régime standard, les chercheurs peuvent maximiser les chances que le niveau global de discipline des individus entre les deux groupes soit à peu près égal.

Ainsi, dans toute expérience utilisant le blocage, il est également important d’attribuer au hasard des individus à des traitements afin de contrôler les effets de toute variable potentielle cachée.

Ressources additionnelles

Variables explicatives et variables de réponse
Variables cachées
Conception de paires assorties
Conception de parcelles divisées