Test exact de Fisher : définition, formule et exemple
Le test exact de Fisher est utilisé pour déterminer s’il existe ou non une association significative entre deux variables catégorielles. Il est généralement utilisé comme alternative au test d’indépendance du chi carré lorsqu’un ou plusieurs comptes de cellules dans un tableau 2 × 2 sont inférieurs à 5.
Le test exact de Fisher utilise les hypothèses nulles et alternatives suivantes :
- H 0 : (hypothèse nulle) Les deux variables sont indépendantes.
- H 1 : (hypothèse alternative) Les deux variables ne sont pas indépendantes.
Supposons que nous ayons le tableau 2×2 suivant :
| Groupe 1 | Groupe 2 | Total de la ligne | |
| Catégorie 1 | un | b | a+b |
| Catégorie 2 | c | d | c+d |
| Total de la colonne | a+c | b+d | a+b+c+d = n |
La valeur p unilatérale pour le test exact de Fisher est calculée comme suit :
p = (a+b)!(c+d)!(a+c)!(b+d)! / (a!b!c!d!n!)
Cela produit la même valeur p que le CDF de la distribution hypergéométrique avec les paramètres suivants :
- taille de la population = n
- « succès » de la population = a+b
- taille de l’échantillon = a + c
- exemples de « succès » = un
La valeur p bilatérale pour le test exact de Fisher est moins simple à calculer et ne peut pas être trouvée en multipliant simplement la valeur p unilatérale par deux. Pour trouver la valeur p bilatérale, nous vous recommandons d’utiliser le calculateur de test exact de Fisher .
Test exact de Fisher : exemple
Supposons que nous voulions savoir si le genre est associé ou non à la préférence pour un parti politique. Nous prenons un échantillon aléatoire simple de 25 électeurs et les interrogeons sur leur préférence en matière de parti politique. Le tableau suivant présente les résultats de l’enquête :
| Démocrate | Républicain | Total | |
| Mâle | 4 | 9 | 13 |
| Femelle | 8 | 4 | 12 |
| Total | 12 | 13 | 25 |
Étape 1 : Définir les hypothèses.
Nous effectuerons le test exact de Fisher en utilisant les hypothèses suivantes :
- H 0 : Le sexe et les préférences en matière de parti politique sont indépendants.
- H 1 : Le sexe et les préférences en matière de parti politique ne sont pas indépendants.
Étape 2 : Calcul de la valeur p bilatérale.
Nous pouvons utiliser le calculateur de test exact de Fisher avec l’entrée suivante :
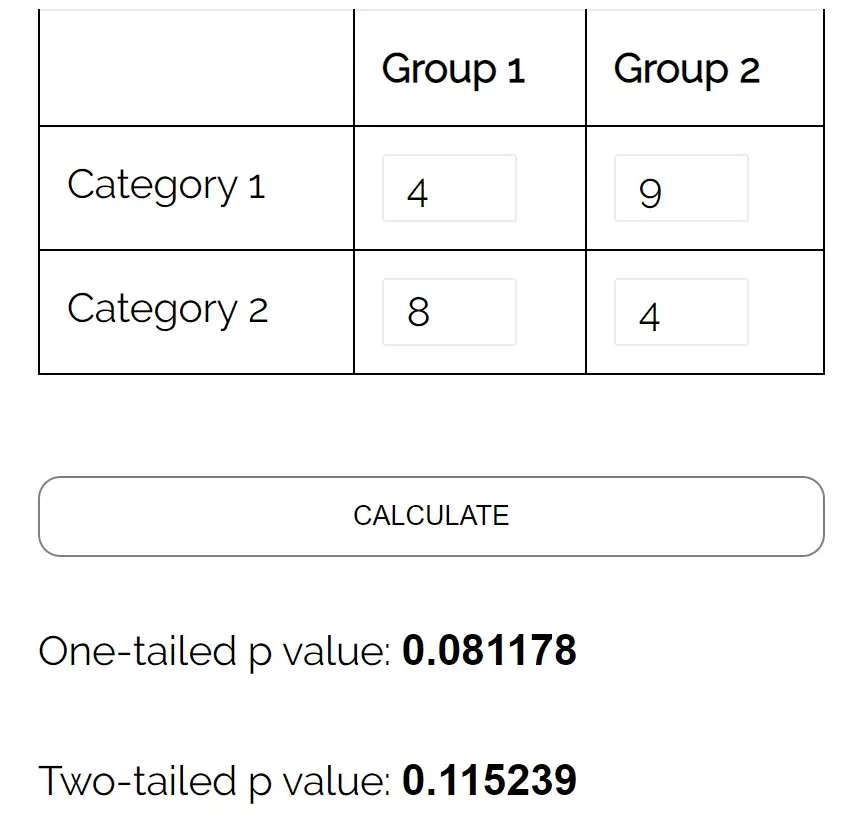
La valeur p bilatérale est 0,115239 . Cette valeur étant inférieure à 0,05, nous ne parvenons pas à rejeter l’hypothèse nulle. Nous ne disposons pas de preuves suffisantes pour affirmer qu’il existe une association statistiquement significative entre le sexe et la préférence pour un parti politique.
Ressources additionnelles
Les didacticiels suivants expliquent comment effectuer un test exact de Fisher à l’aide de différents programmes statistiques :
Comment effectuer le test exact de Fisher dans R
Comment effectuer le test exact de Fisher dans Excel
Comment effectuer le test exact de Fisher dans Stata
Comment effectuer le test exact de Fisher dans SPSS
Comment effectuer le test exact de Fisher en Python
Calculateur de test exact de Fisher
