Théorème central limite
Cet article explique ce qu’est le théorème central limite (CLT) et à quoi il sert en statistiques. Vous trouverez également quelle est la formule du théorème central limite et un exemple de son application résolu étape par étape.
Quel est le théorème central limite ?
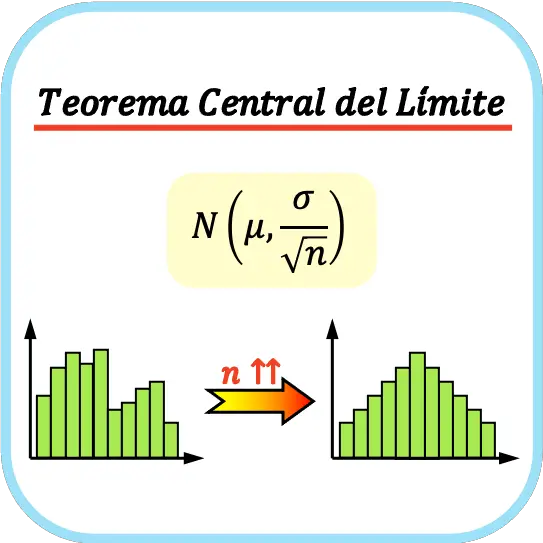
En statistique, le théorème central limite , également appelé théorème central limite , stipule que la distribution des moyennes de l’échantillon se rapproche d’une distribution normale à mesure que la taille de l’échantillon augmente, quelle que soit la distribution de probabilité de la population.
Autrement dit, le théorème central limite dit que si nous prenons un nombre suffisamment grand d’échantillons, la moyenne de ces échantillons peut être approchée d’une distribution normale.
De plus, le théorème central limite stipule que la moyenne de l’échantillon se rapprochera de la valeur de la moyenne de la population à mesure que la taille de l’échantillon augmente. Cela nous permet d’approcher les paramètres de la population statistique. Ci-dessous, nous verrons comment cela se fait.
En général, on considère que pour appliquer le théorème central limite, la taille de l’échantillon doit être d’au moins 30 observations, bien que cela dépende des caractéristiques de la variable étudiée.
Le théorème central limite a de nombreuses applications, puisque la distribution normale permet des calculs statistiques inférentiels, tels que des tests d’hypothèses ou des intervalles de confiance. Par exemple, en finance, le théorème central limite est utilisé pour analyser le rendement et le risque d’un investissement.
Exemple du théorème central limite
Une fois que nous avons vu la définition du théorème central limite, regardons un exemple pour bien comprendre sa signification.
Un exemple du théorème central limite est le lancement d’un dé. Le lancer de dé suit une distribution uniforme discrète , puisque tous les résultats sont équiprobables. Mais la distribution de la somme de plusieurs résultats se rapproche d’une distribution normale.
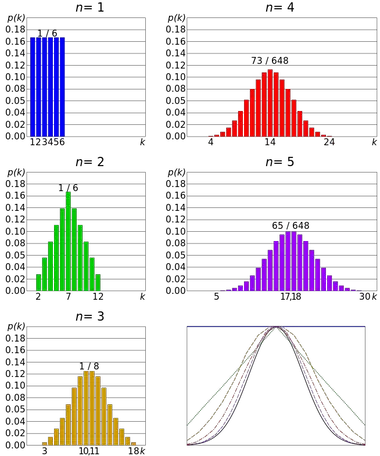
Ainsi, plus il y a de lancers, plus il est probable que la forme de la distribution des moyennes aura tendance à ressembler au graphique de la distribution normale.
Formule du théorème central limite
Le théorème central limite stipule que si une population a une moyenne μ et un écart type σ et que nous prenons un nombre suffisamment grand d’échantillons (n≥30), l’ensemble des moyennes d’échantillon peut être approché d’une distribution normale de moyenne μ et standard écart σ/√n.
![]()
De plus , si X 1 , à une distribution normale définie par la formule suivante :
![]()
Exercice résolu du théorème central limite
Pour que vous puissiez bien assimiler le concept, voici un exercice résolu du théorème central limite.
- Une entreprise vend des pièces qui servent à remplacer certains composants de jouets. Une pièce a un poids moyen de 300 g et un écart type de 50 g. Si un client a commandé un lot de 100 pièces, quelle est la probabilité que le poids moyen des pièces du lot soit supérieur à 305 g ? Et quelle est la probabilité qu’un lot de 100 pièces pèse plus de 31 kg ?
Puisque la taille du lot est grande (n=100), nous pouvons appliquer le théorème central limite pour résoudre le problème.
Ainsi, en utilisant la formule du théorème central limite, la distribution des moyennes de l’échantillon peut être approchée d’une distribution normale avec les paramètres suivants :
![]()
![]()
![]()
![]()
Maintenant, nous effectuons le processus de typage pour pouvoir ensuite trouver la probabilité que l’exercice nous demande. Pour ce faire, nous devons soustraire la moyenne de la distribution puis diviser par l’écart type :
![]()
Ainsi, pour trouver la probabilité que le poids moyen des pièces du lot soit supérieur à 305 g, il faut regarder à quelle valeur Z>1 correspond dans le tableau de distribution normale :
![]()
En revanche, grâce au théorème central limite on peut savoir qu’un lot de 100 pièces peut se rapprocher d’une distribution normale, puisque toutes les pièces suivent la même distribution. Par conséquent, pour déterminer la probabilité qu’un lot de 100 pièces pèse plus de 31 kg, nous devons appliquer l’autre formule du théorème central limite :
![]()
![]()
![]()
Nous refaisons donc le processus de typage, puis trouvons la deuxième probabilité que le problème nous demande :
![]()
Enfin, nous pouvons déterminer la probabilité qu’un lot de 100 pièces pèse plus de 31 kg en utilisant le tableau de distribution normale :
![]()
