Comment trouver les valeurs aberrantes à l’aide de l’intervalle interquartile

Une valeur aberrante est une observation anormalement éloignée des autres valeurs d’un ensemble de données. Les valeurs aberrantes peuvent poser problème car elles peuvent affecter les résultats d’une analyse.

Une façon courante de détecter les valeurs aberrantes dans un ensemble de données consiste à utiliser l’ intervalle interquartile .

L’intervalle interquartile, souvent abrégé IQR, est la différence entre le 25e centile (Q1) et le 75e centile (Q3) dans un ensemble de données. Il mesure la répartition des 50 % moyens des valeurs.

Une méthode populaire consiste à déclarer une observation comme valeur aberrante si elle a une valeur 1,5 fois supérieure à l’IQR ou 1,5 fois inférieure à l’IQR.

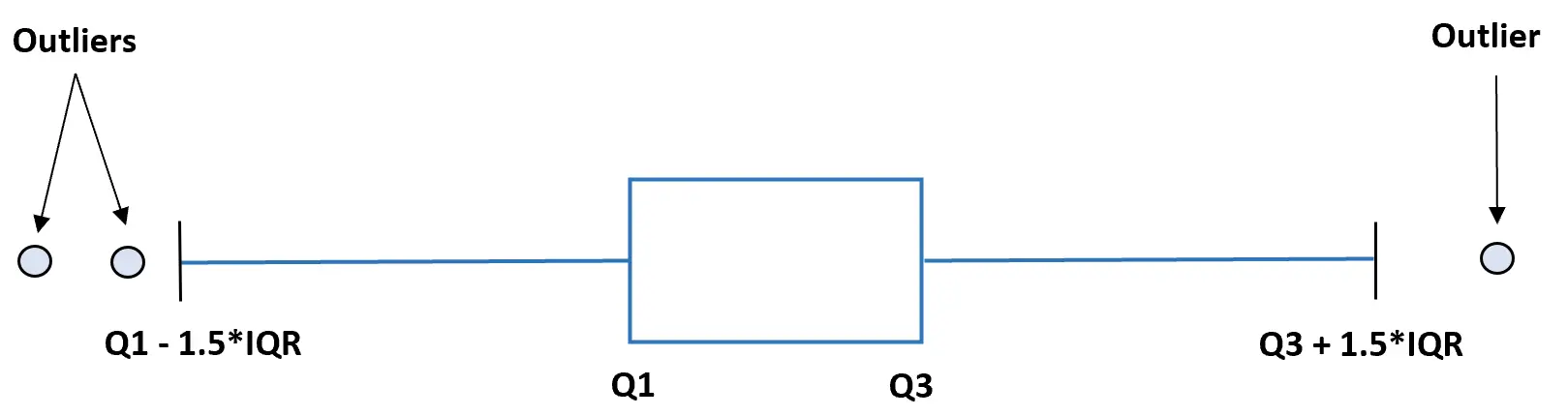
Ce didacticiel fournit un exemple étape par étape de la manière de rechercher des valeurs aberrantes dans un ensemble de données à l’aide de cette méthode.

Étape 1 : Créer les données

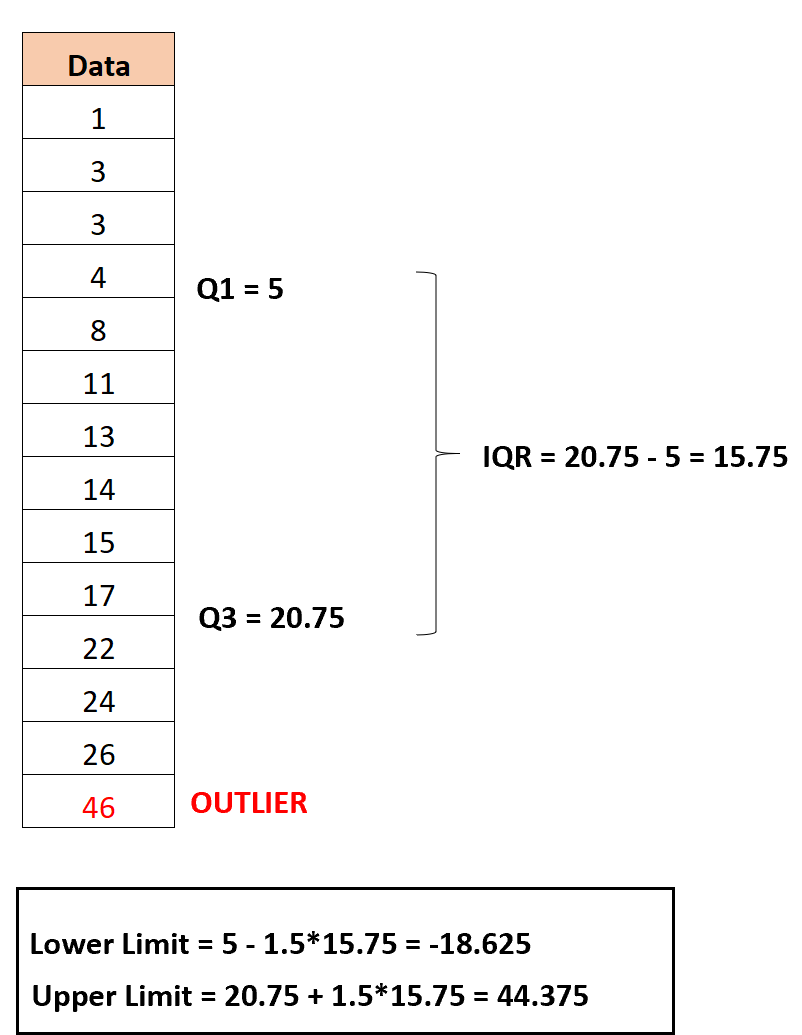
Supposons que nous ayons l’ensemble de données suivant :

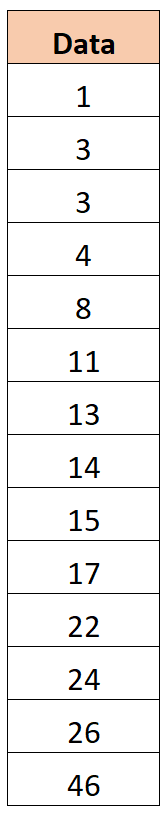
Étape 2 : Identifiez le premier et le troisième quartile

Le premier quartile s’avère être 5 et le troisième quartile s’avère être 20,75 .

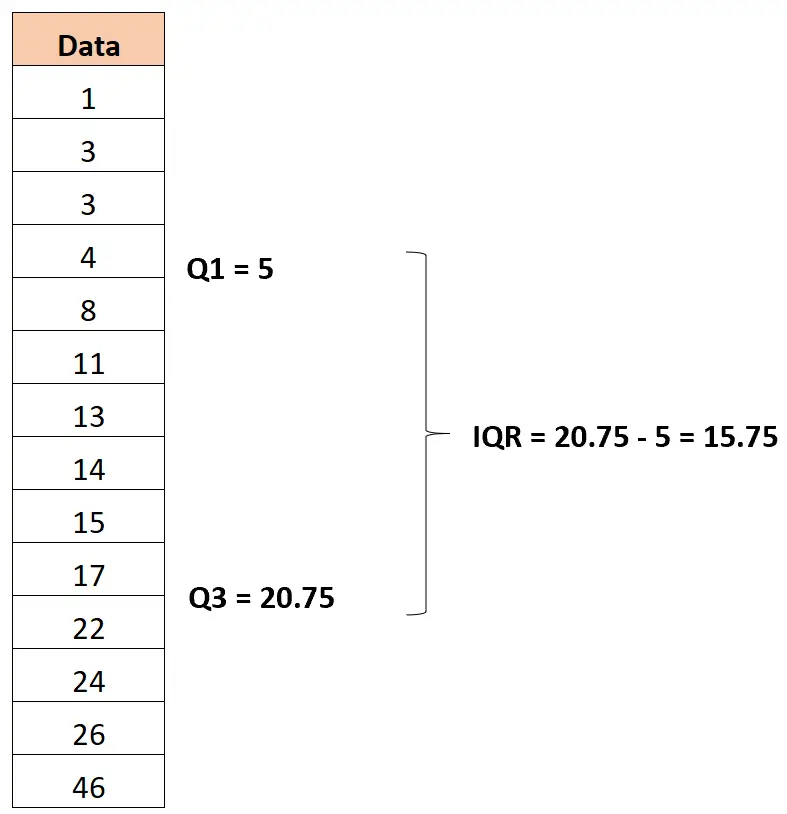
Ainsi, l’intervalle interquartile s’avère être 20,75 -5 = 15,75 .

Étape 3 : Trouver les limites inférieure et supérieure

La limite inférieure est calculée comme suit :

Limite inférieure = Q1 – 1,5*IQR = 5 – 1,5*15,75 = -18,625

Et la limite supérieure est calculée comme suit :

Limite supérieure = Q3 + 1,5*IQR = 20,75 + 1,5*15,75 = 44,375

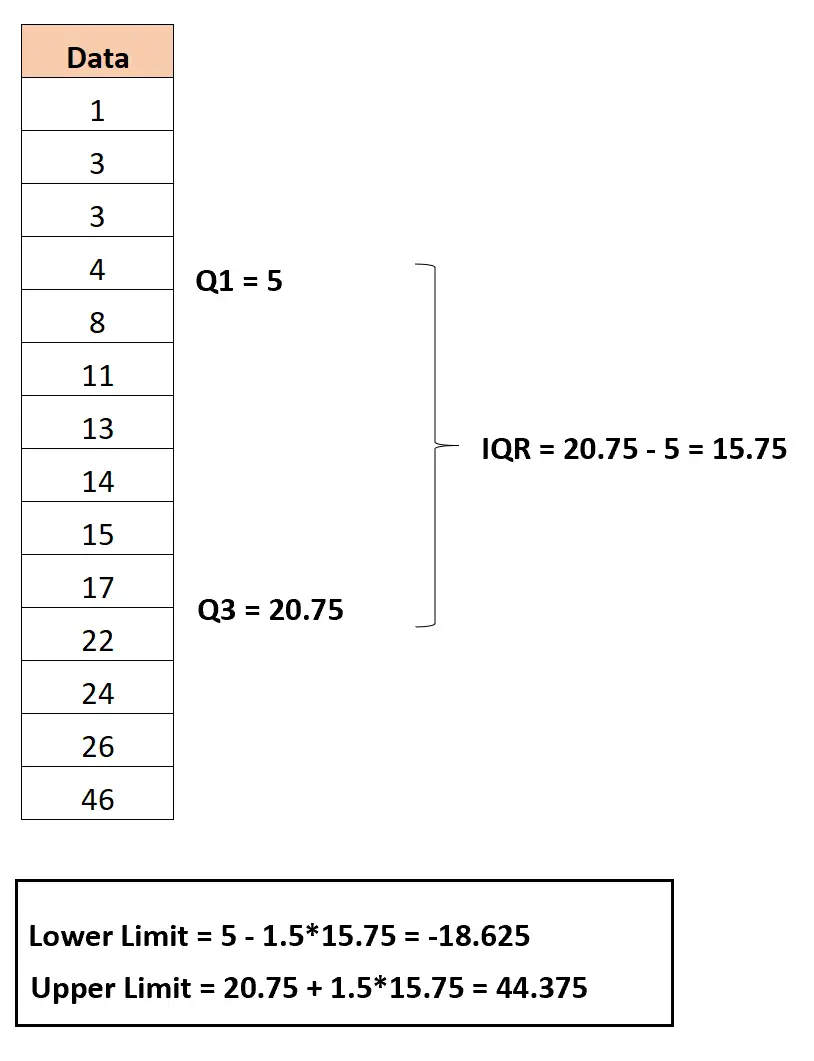
Étape 4 : Identifiez les valeurs aberrantes

La seule observation dans l’ensemble de données avec une valeur inférieure à la limite inférieure ou supérieure à la limite supérieure est 46 . Il s’agit donc de la seule valeur aberrante dans cet ensemble de données.

Remarque : Vous pouvez utiliser ce calculateur de limites aberrantes pour rechercher automatiquement les limites supérieure et inférieure des valeurs aberrantes dans un ensemble de données donné.

Comment trouver les valeurs aberrantes dans la pratique

Les didacticiels suivants expliquent comment rechercher des valeurs aberrantes à l’aide de l’intervalle interquartile dans différents logiciels statistiques :

Comment trouver les valeurs aberrantes dans Excel
Comment trouver les valeurs aberrantes dans R
Comment trouver les valeurs aberrantes en Python
Comment trouver les valeurs aberrantes dans SPSS