Que sont les variables dichotomiques ? (Définition & #038; Exemple)

Une variable dichotomique est un type de variable qui ne prend que deux valeurs possibles.

Voici quelques exemples de variables dichotomiques :

• Sexe : Homme ou Femme
• Coin Flip : Pile ou Face
• Type de propriété : Résidentielle ou Commerciale
• Statut d’athlète : Professionnel ou Amateur
• Résultats de l’examen : réussite ou échec

Ces types de variables surviennent tout le temps dans la pratique. Par exemple, considérons l’ensemble de données suivant qui contient 10 observations et 4 variables :

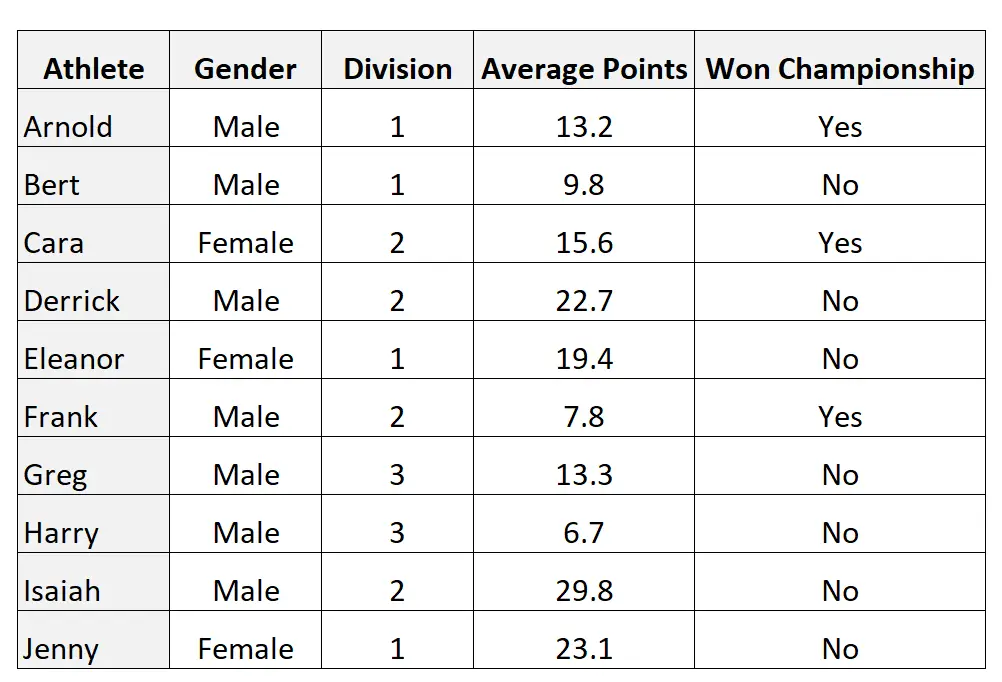
Les variables genre et Championnat gagné sont dichotomiques car elles ne peuvent prendre chacune que deux valeurs possibles :

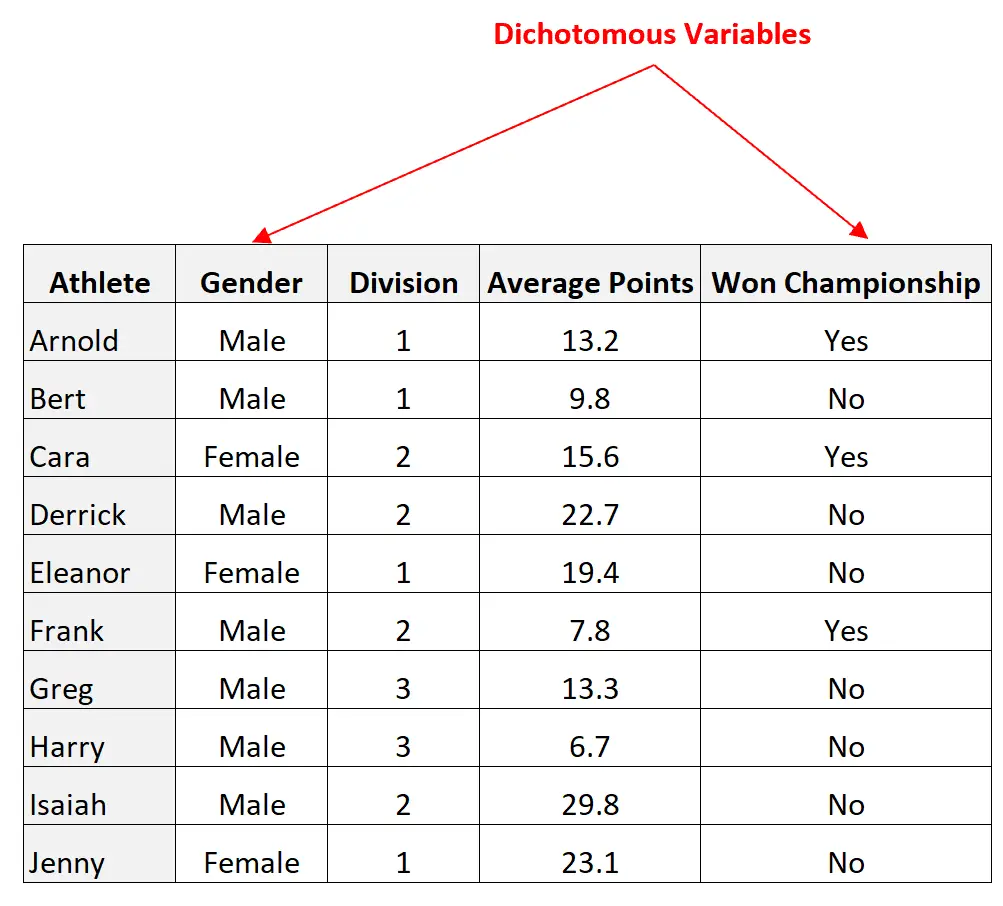
Cependant, les variables Division et Moyenne de points ne sont pas dichotomiques car elles peuvent prendre plusieurs valeurs.

Astuce bonus :

Vous pouvez vous rappeler que les variables dichotomiques ne peuvent prendre que deux valeurs en vous rappelant que le préfixe « di » est un mot grec qui signifie « deux », « deux fois » ou « double ».

Comment créer des variables dichotomiques

Il convient de noter que nous pouvons créer une variable dichotomique à partir d’une variable continue en séparant simplement les valeurs en fonction d’un certain seuil.

Par exemple, dans l’ensemble de données précédent, nous pourrions transformer la variable Points moyens en une variable dichotomique en classant les joueurs avec une moyenne supérieure à 15 comme « bons buteurs » et ceux avec une moyenne inférieure à 15 comme « mauvais buteurs » :

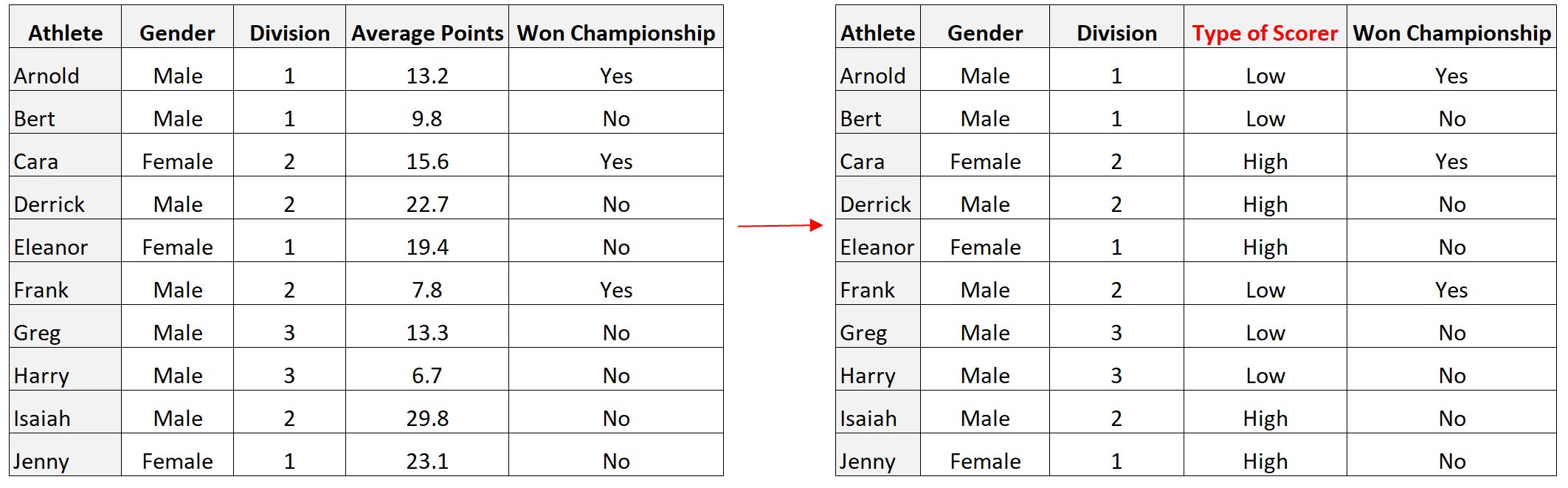
Comment visualiser les variables dichotomiques

Nous visualisons généralement les variables dichotomiques en utilisant un simple graphique à barres pour représenter les fréquences de chaque valeur qu’elles peuvent prendre.

Par exemple, le graphique à barres suivant montre les fréquences de chaque sexe dans l’ensemble de données précédent :

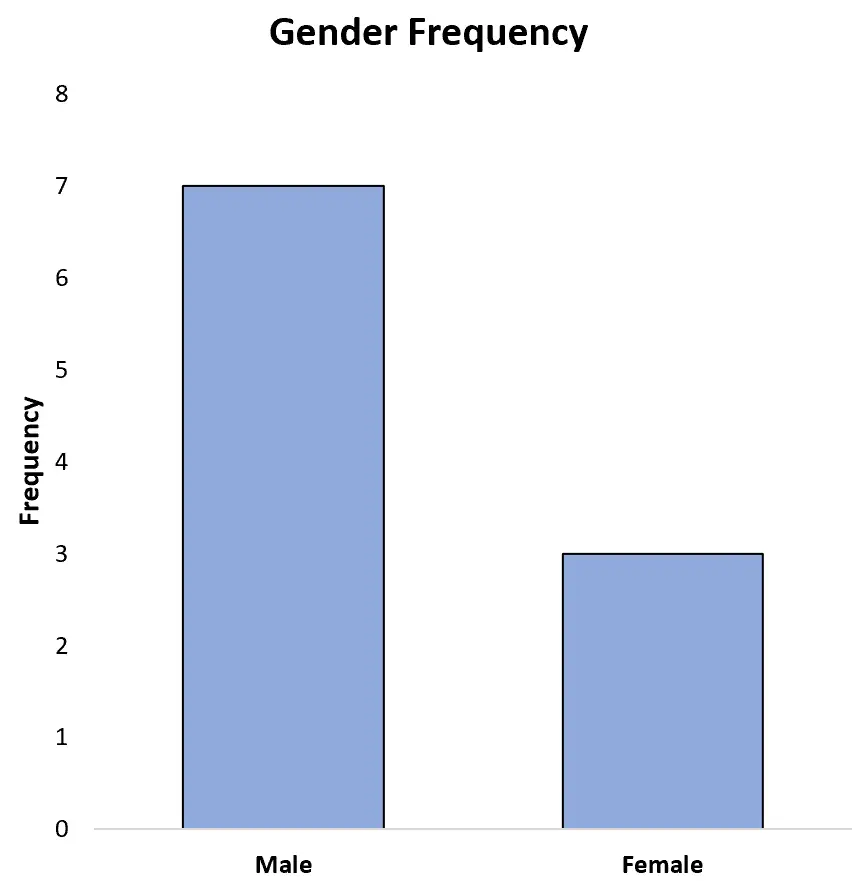
Nous pourrions également afficher les fréquences sous forme de pourcentages sur l’axe des y :

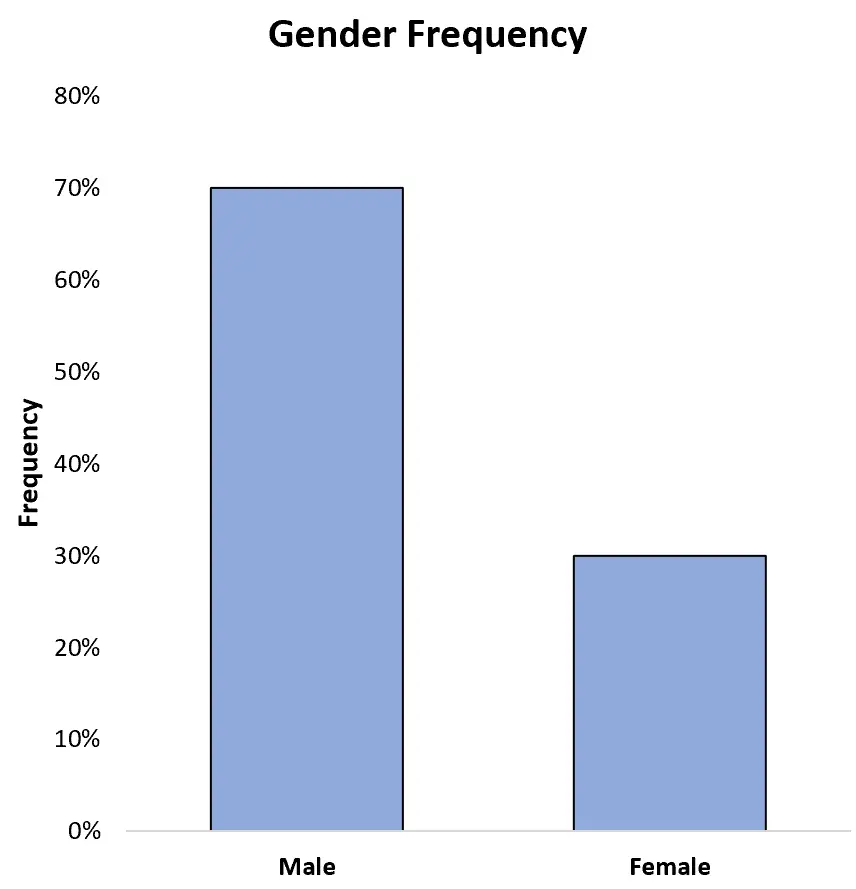
Cela nous permet de voir facilement que 70 % du total des athlètes de l’ensemble de données sont des hommes et 30 % sont des femmes.

Comment analyser les variables dichotomiques

Il existe plusieurs façons d’analyser les variables dichotomiques. Deux des méthodes les plus courantes incluent :

1. Test z à une proportion

Un test z à une proportion détermine si une proportion observée est égale ou non à une proportion théorique.

Par exemple, nous pourrions utiliser ce test pour déterminer si la véritable proportion d’athlètes masculins dans une population donnée est égale à 50 %.

2. Corrélation point-bisériale

La corrélation point-bisériale est utilisée pour mesurer la relation entre une variable dichotomique et une variable continue.

Ce type de corrélation prend une valeur comprise entre -1 et 1 où :

• -1 indique une corrélation parfaitement négative entre deux variables
• 0 indique aucune corrélation entre deux variables
• 1 indique une corrélation parfaitement positive entre deux variables

Par exemple, nous pourrions calculer la corrélation point-bisériale entre le sexe et la moyenne de points par match pour comprendre dans quelle mesure ces deux variables sont liées.