Comment effectuer une régression linéaire simple dans R (étape par étape)

La régression linéaire simple est une technique que nous pouvons utiliser pour comprendre la relation entre une seule variable explicative et une seule variable de réponse .

En un mot, cette technique trouve une ligne qui « correspond » le mieux aux données et prend la forme suivante :

ŷ = b ₀ + b ₁ x

où:

• ŷ : La valeur de réponse estimée
• b ₀ : L’origine de la droite de régression
• b ₁ : La pente de la droite de régression

Cette équation peut nous aider à comprendre la relation entre la variable explicative et la variable de réponse et (en supposant qu’elle soit statistiquement significative) elle peut être utilisée pour prédire la valeur d’une variable de réponse étant donné la valeur de la variable explicative.

Ce didacticiel fournit une explication étape par étape sur la façon d’effectuer une régression linéaire simple dans R.

Étape 1 : Charger les données

Pour cet exemple, nous allons créer un faux ensemble de données contenant les deux variables suivantes pour 15 étudiants :

• Nombre total d’heures étudiées pour certains examens
• Résultat de l’examen

Nous tenterons d’adapter un modèle de régression linéaire simple en utilisant les heures comme variable explicative et les résultats de l’examen comme variable de réponse.

Le code suivant montre comment créer ce faux ensemble de données dans R :

#create dataset
df <- data.frame(hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1     1    64
2     2    66
3     4    76
4     5    73
5     5    74
6     6    81

#attach dataset to make it more convenient to work with
attach(df)

Étape 2 : Visualisez les données

Avant d’ajuster un modèle de régression linéaire simple, nous devons d’abord visualiser les données pour les comprendre.

Premièrement, nous voulons nous assurer que la relation entre les heures et le score est à peu près linéaire, car il s’agit d’une hypothèse sous-jacente massive de régression linéaire simple. Nous pouvons créer un nuage de points simple pour visualiser la relation entre les deux variables :

scatter.smooth(hours, score, main='Hours studied vs. Exam Score')

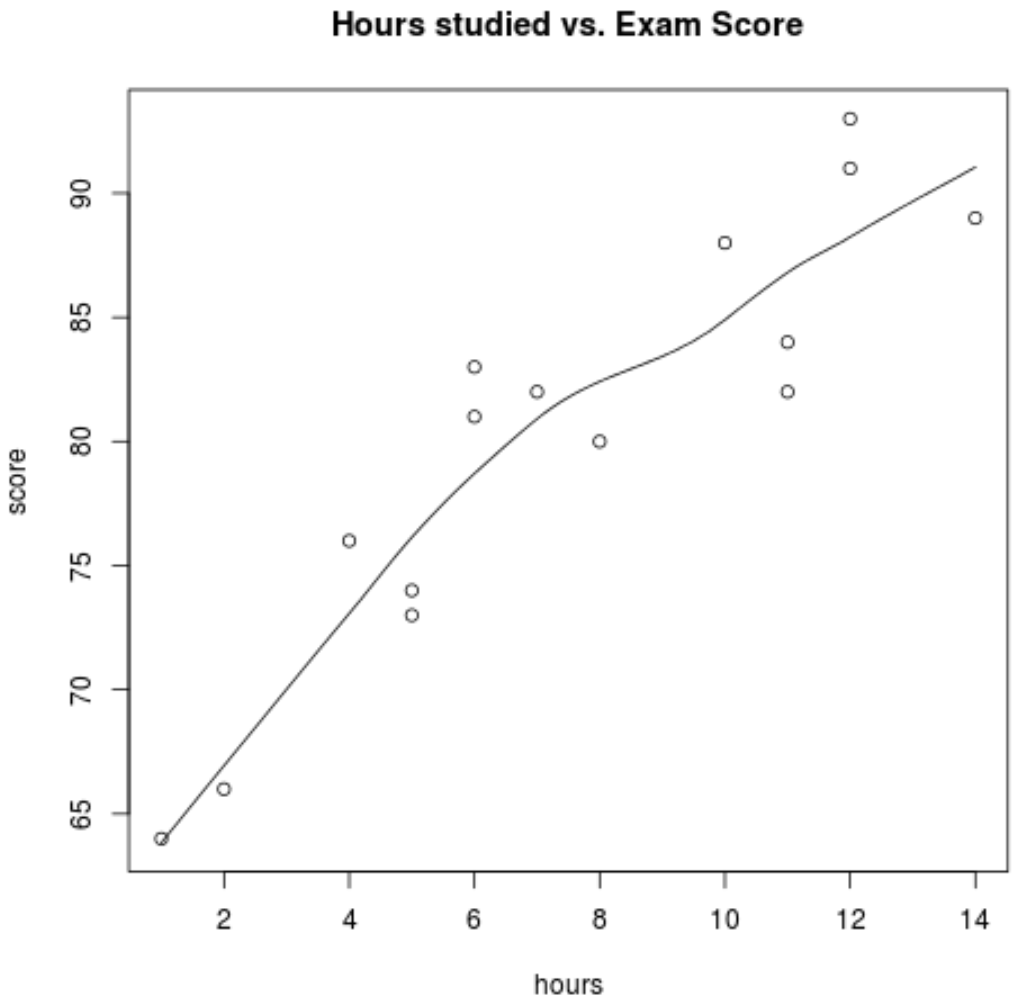
D’après le graphique, nous pouvons voir que la relation semble être linéaire. À mesure que le nombre d’heures augmente, le score a également tendance à augmenter de manière linéaire.

Ensuite, nous pouvons créer un boxplot pour visualiser la distribution des résultats des examens et vérifier les valeurs aberrantes . Par défaut, R définit une observation comme étant aberrante si elle est 1,5 fois l’intervalle interquartile supérieur au troisième quartile (Q3) ou 1,5 fois l’intervalle interquartile inférieur au premier quartile (Q1).

Si une observation est aberrante, un petit cercle apparaîtra dans le boxplot :

boxplot(score)

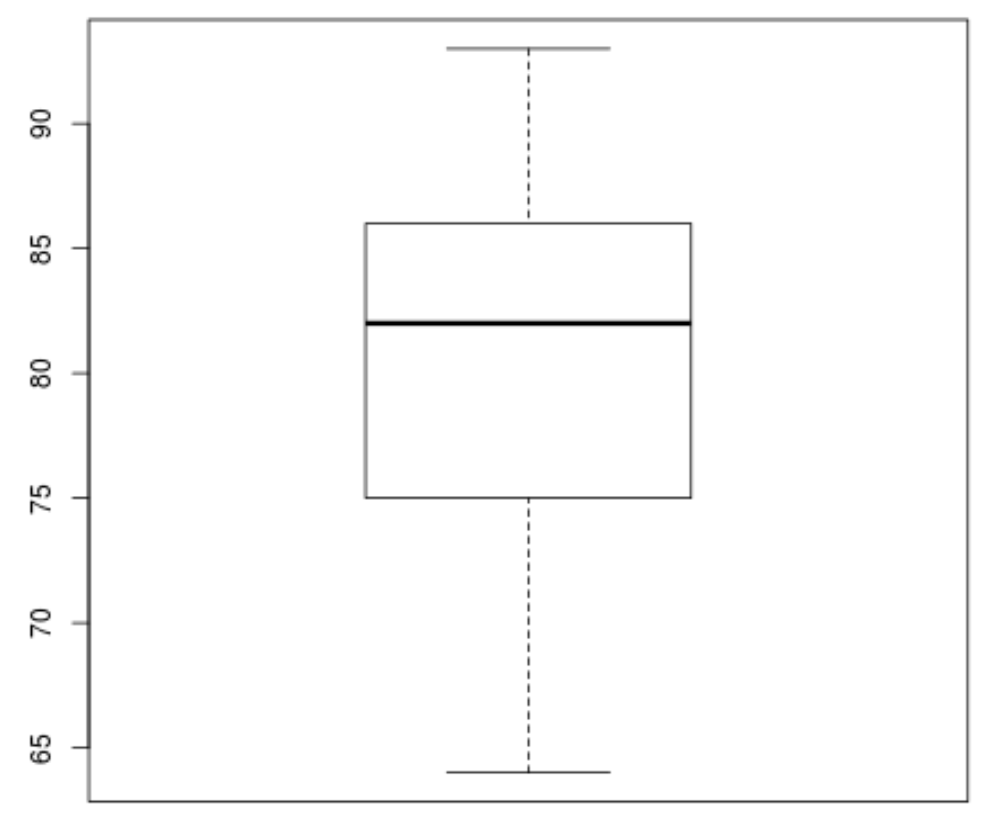
Il n’y a pas de petits cercles dans le boxplot, ce qui signifie qu’il n’y a pas de valeurs aberrantes dans notre ensemble de données.

Étape 3 : Effectuer une régression linéaire simple

Une fois que nous avons confirmé que la relation entre nos variables est linéaire et qu’il n’y a pas de valeurs aberrantes, nous pouvons procéder à l’ajustement d’un modèle de régression linéaire simple en utilisant les heures comme variable explicative et le score comme variable de réponse :

#fit simple linear regression model
model <- lm(score~hours)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min     1Q Median     3Q    Max 
-5.140 -3.219 -1.193  2.816  5.772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   65.334      2.106  31.023 1.41e-13 ***
hours          1.982      0.248   7.995 2.25e-06 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared:  0.831,	Adjusted R-squared:  0.818 
F-statistic: 63.91 on 1 and 13 DF,  p-value: 2.253e-06

À partir du résumé du modèle, nous pouvons voir que l’équation de régression ajustée est :

Score = 65,334 + 1,982*(heures)

Cela signifie que chaque heure supplémentaire étudiée est associée à une augmentation moyenne de la note à l’examen de 1,982 points. Et la valeur d’origine de 65,334 nous indique la note moyenne attendue à l’examen pour un étudiant qui étudie zéro heure.

Nous pouvons également utiliser cette équation pour trouver la note attendue à l’examen en fonction du nombre d’heures qu’un étudiant étudie. Par exemple, un étudiant qui étudie pendant 10 heures devrait obtenir une note à l’examen de 85,15 :

Note = 65,334 + 1,982*(10) = 85,15

Voici comment interpréter le reste du résumé du modèle :

• Pr(>|t|) : Il s’agit de la valeur p associée aux coefficients du modèle. Étant donné que la valeur p pour les heures (2,25e-06) est nettement inférieure à 0,05, nous pouvons dire qu’il existe une association statistiquement significative entre les heures et le score .
• R-carré multiple : ce nombre nous indique que le pourcentage de variation des résultats de l’examen peut s’expliquer par le nombre d’heures étudiées. En général, plus la valeur R au carré d’un modèle de régression est grande, plus les variables explicatives sont capables de prédire la valeur de la variable de réponse. Dans ce cas, 83,1 % de la variation des scores peut être expliquée par les heures étudiées.
• Erreur type résiduelle : il s’agit de la distance moyenne entre les valeurs observées et la ligne de régression. Plus cette valeur est faible, plus une droite de régression est capable de correspondre aux données observées. Dans ce cas, le score moyen observé à l’examen s’écarte de 3,641 points du score prédit par la droite de régression.
• Statistique F et valeur p : La statistique F ( 63,91 ) et la valeur p correspondante ( 2,253e-06 ) nous indiquent la signification globale du modèle de régression, c’est-à-dire si les variables explicatives du modèle sont utiles pour expliquer la variation. dans la variable de réponse. Étant donné que la valeur p dans cet exemple est inférieure à 0,05, notre modèle est statistiquement significatif et les heures sont considérées comme utiles pour expliquer la variation du score .

Étape 4 : Créer des tracés résiduels

Après avoir adapté le modèle de régression linéaire simple aux données, la dernière étape consiste à créer des tracés résiduels.

L’une des hypothèses clés de la régression linéaire est que les résidus d’un modèle de régression sont à peu près normalement distribués et sont homoscédastiques à chaque niveau de la variable explicative. Si ces hypothèses ne sont pas respectées, les résultats de notre modèle de régression pourraient être trompeurs ou peu fiables.

Pour vérifier que ces hypothèses sont remplies, nous pouvons créer les tracés résiduels suivants :

Graphique des valeurs résiduelles par rapport aux valeurs ajustées : ce graphique est utile pour confirmer l’homoscédasticité. L’axe des x affiche les valeurs ajustées et l’axe des y affiche les résidus. Tant que les résidus semblent être répartis de manière aléatoire et uniforme dans tout le graphique autour de la valeur zéro, nous pouvons supposer que l’homoscédasticité n’est pas violée :

#define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

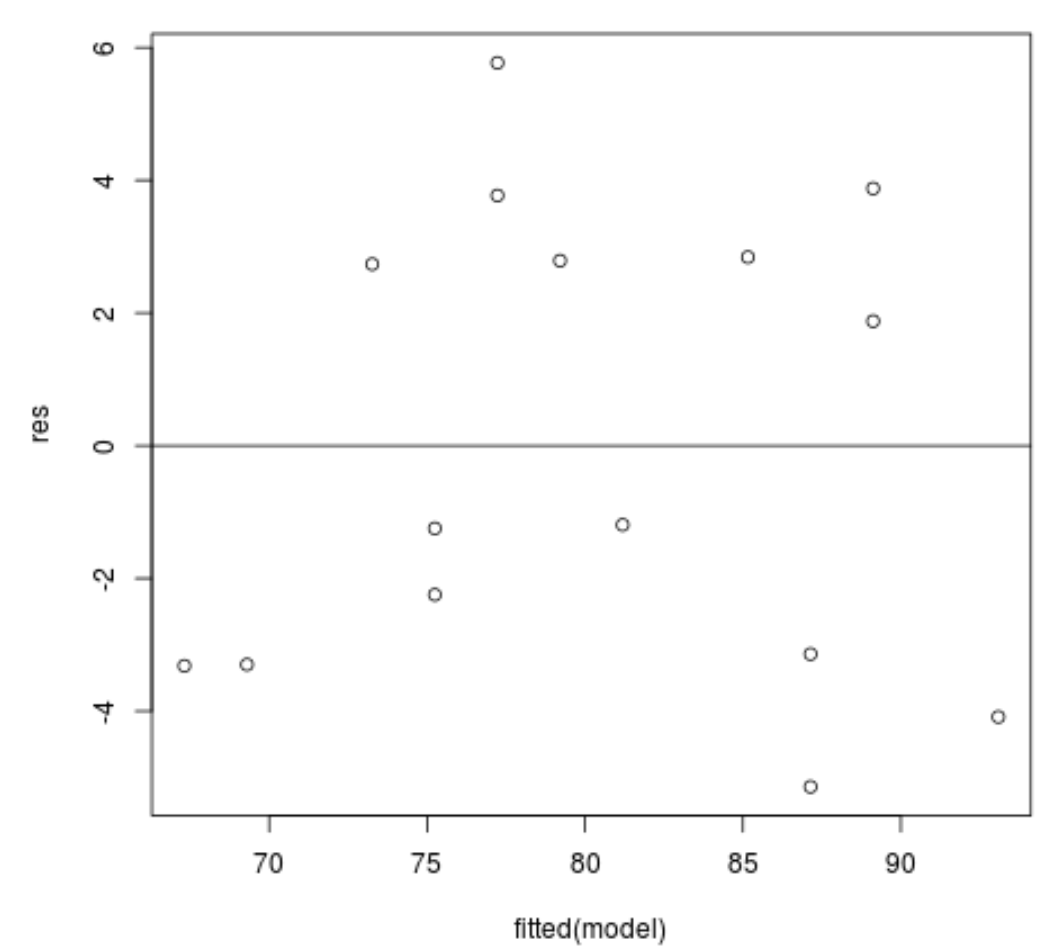
Les résidus semblent être dispersés de manière aléatoire autour de zéro et ne présentent aucun modèle notable, cette hypothèse est donc remplie.

Tracé QQ : ce tracé est utile pour déterminer si les résidus suivent une distribution normale. Si les valeurs des données dans le tracé suivent une ligne à peu près droite à un angle de 45 degrés, alors les données sont normalement distribuées :

#create Q-Q plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

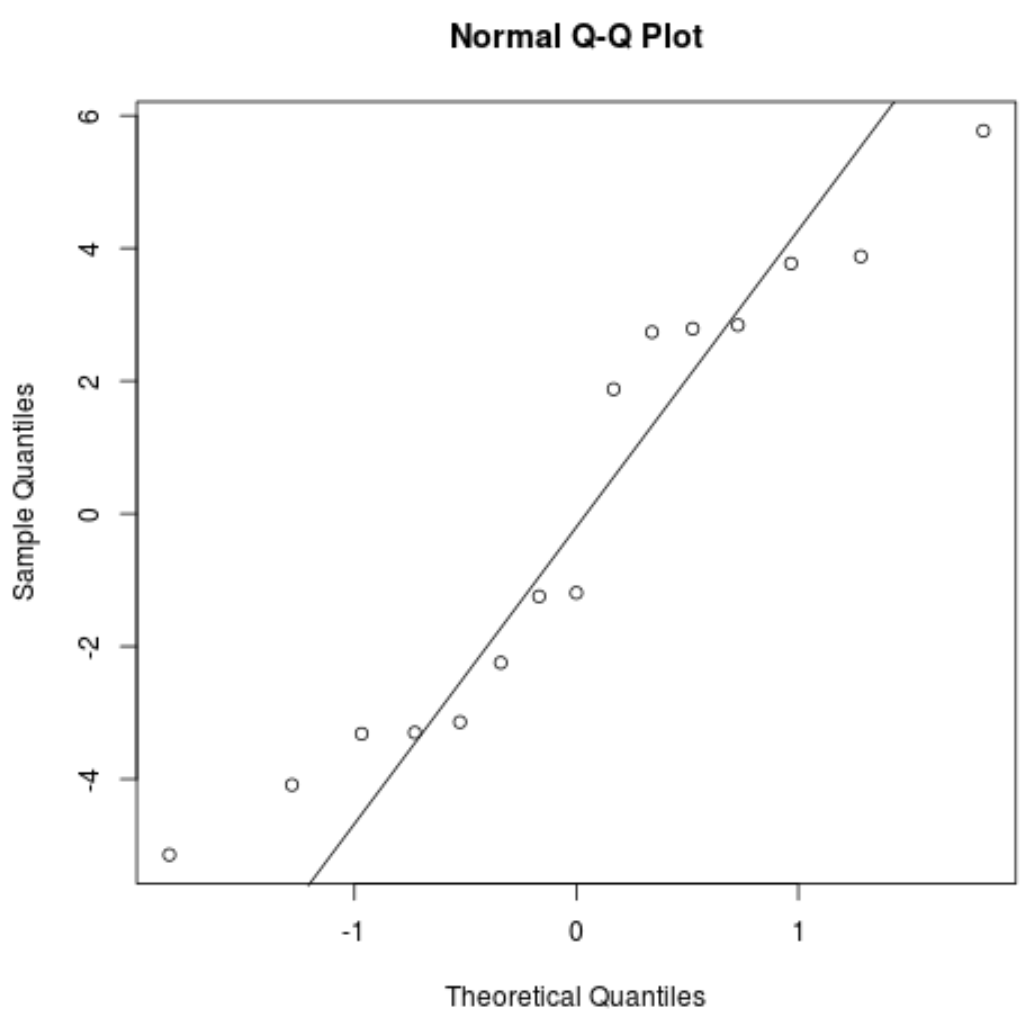
Les résidus s’écartent un peu de la ligne des 45 degrés, mais pas suffisamment pour susciter de sérieuses inquiétudes. Nous pouvons supposer que l’hypothèse de normalité est remplie.

Puisque les résidus sont normalement distribués et homoscédastiques, nous avons vérifié que les hypothèses du modèle de régression linéaire simple sont remplies. Ainsi, la sortie de notre modèle est fiable.

Le code R complet utilisé dans ce tutoriel peut être trouvé ici .