Test de Friedman : définition, formule et exemple

Le test de Friedman est une alternative non paramétrique à l’ ANOVA à mesures répétées .

Il est utilisé pour déterminer s’il existe ou non une différence statistiquement significative entre les moyennes de trois groupes ou plus dans lesquels les mêmes sujets apparaissent dans chaque groupe.

Quand utiliser le test de Friedman

Le test de Friedman est couramment utilisé dans deux situations :

1. Mesurer les scores moyens des sujets sur trois points temporels ou plus.

Par exemple, vous souhaiterez peut-être mesurer la fréquence cardiaque au repos des sujets un mois avant de commencer un programme d’entraînement, un mois après le début du programme et deux mois après avoir utilisé le programme. Vous pouvez effectuer le test de Friedman pour voir s’il existe une différence significative dans la fréquence cardiaque moyenne au repos des patients à ces trois moments.

2. Mesurer les scores moyens des sujets dans trois conditions différentes.

Par exemple, vous pourriez demander à des sujets de regarder trois films différents et d’évaluer chacun d’entre eux en fonction de leur appréciation. Étant donné que chaque sujet apparaît dans chaque échantillon, vous pouvez effectuer un test de Friedman pour voir s’il existe une différence significative dans la note moyenne des trois films.

Test de Friedman : exemple

Supposons que nous voulions savoir si le temps de réaction moyen des sujets est différent sur trois médicaments différents. Pour tester cela, nous recrutons 10 patients et mesurons chacun de leurs temps de réaction (en secondes) aux trois médicaments différents. Les résultats pour chaque patient sont présentés ci-dessous :

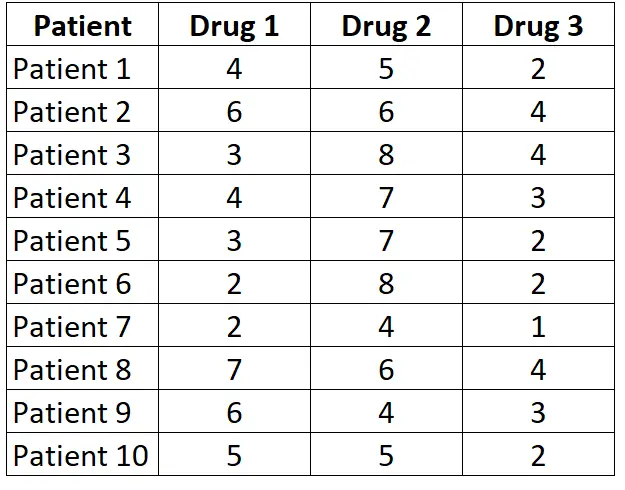
Puisque chaque patient est mesuré sur chacun des trois médicaments, nous utiliserons le test de Friedman pour déterminer si le temps de réaction moyen diffère entre les trois médicaments.

Étape 1. Énoncez les hypothèses.

L’hypothèse nulle (H ₀ ) : µ ₁ = µ ₂ = µ ₃ (les temps de réaction moyens à travers les populations sont tous égaux)

L’hypothèse alternative : (Ha) : au moins une moyenne de population est différente du reste

Étape 2. Effectuez le test de Friedman.

Nous utiliserons la calculatrice de test de Friedman en utilisant l’entrée suivante :

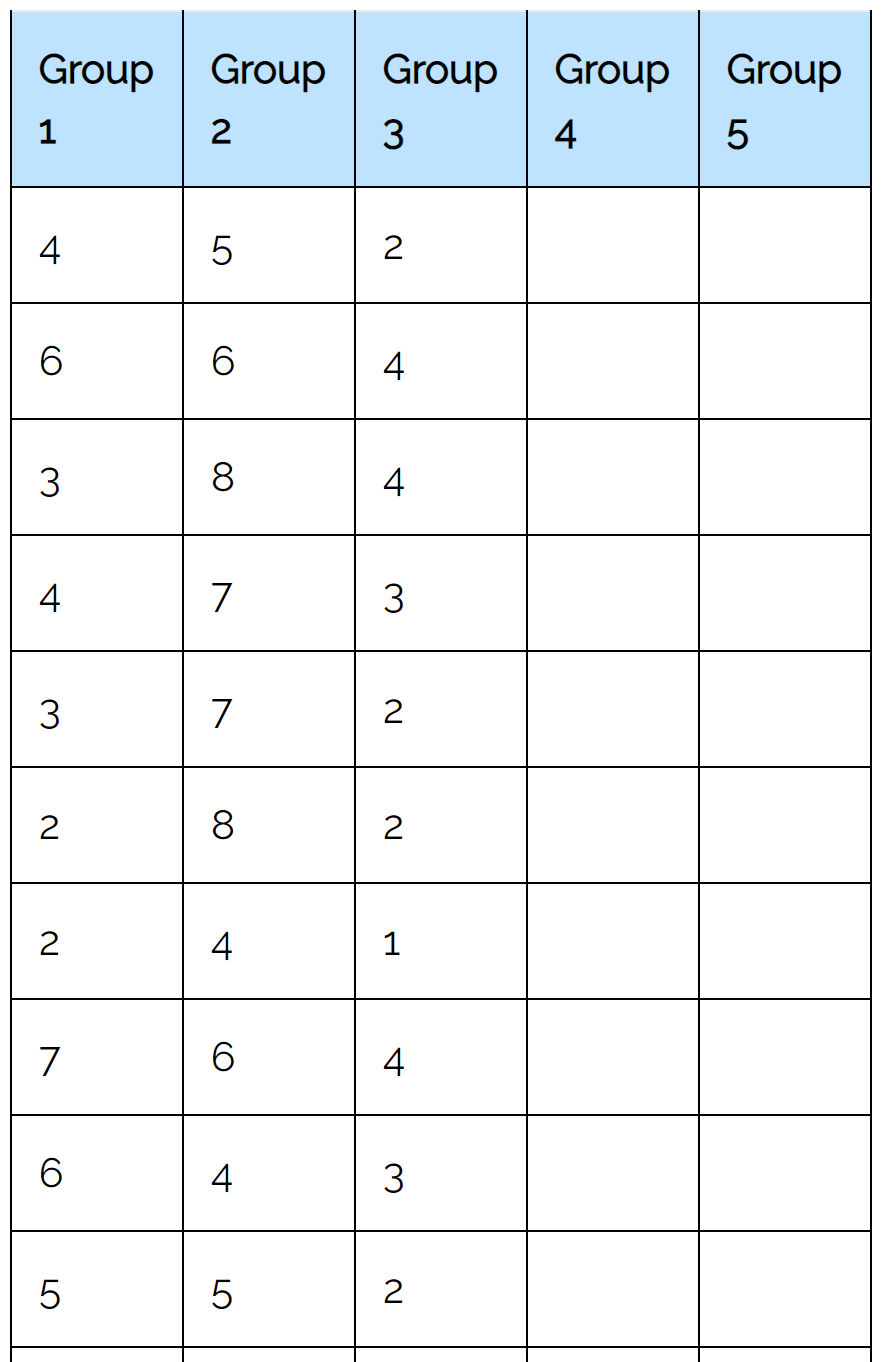
Une fois que nous cliquons sur « Calculer », le résultat suivant apparaîtra automatiquement :

Étape 3 : Interprétez les résultats.

La statistique de test est Q = 12,35 et la valeur p correspondante est p = 0,00208 . Cette valeur étant inférieure à 0,05, nous pouvons rejeter l’hypothèse nulle selon laquelle le temps de réponse moyen est le même pour les trois médicaments.

Nous disposons de suffisamment de preuves pour conclure que le type de médicament utilisé entraîne des différences statistiquement significatives dans le temps de réponse.

Étape 4 : Rapportez les résultats.

Enfin, nous souhaitons rapporter les résultats du test. Voici un exemple de la façon de procéder :

Un test de Friedman a été réalisé sur 10 patients pour examiner l’effet de trois médicaments différents sur le temps de réponse. Chaque patient a utilisé chaque médicament une fois.

Les résultats ont montré que le type de médicament utilisé entraînait des différences statistiquement significatives dans le temps de réponse (Q = 12,35, p = 0,00208).

Ressources additionnelles

Les tutoriels suivants expliquent comment réaliser le test de Friedman à l’aide de différents logiciels statistiques :

Comment effectuer le test de Friedman dans Excel
Comment effectuer le test de Friedman dans R
Comment effectuer le test de Friedman en Python
Comment effectuer le test de Friedman dans Stata
Calculateur de test de Friedman en ligne